hellog〜英語史ブログ / 2012-05-09
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
2012-05-09 Wed
■ #1108. 言語記号の恣意性,有縁性,無縁性 [semantics][semantic_change][language_change][arbitrariness][sound_symbolism][phonaesthesia][onomatopoeia][saussure][sign][root_creation]
ソシュール (Ferdinand de Saussure; 1857--1913) が言語の恣意性 (arbitrariness) を公準として唱えて以来,恣意性を巡る無数の論争が繰り返されてきた.例えば,恣意性の原理に反するものとして,オノマトペ (onomatopoeia) や音象徴 (sound_symbolism) がしばしば挙げられてきた.しかし,ギローは,これらの論争は不毛であり,規約性と有縁性という2つの異なる性質を区別すれば解決する問題だと主張した.
ギロー (24--27) によれば,記号の本質として規約性があることは疑い得ない.記号の signifiant と signifié は,常に社会的な規約によって結びつけられている.規約による結合というと,「でたらめ」や「ランダム」のような恣意性を思い浮かべるかもしれないが,必ずしも有縁性を排除するわけではない.むしろ,「どんな語もみな語源的には有縁的である」 (25) .有縁的というときには,自然的有縁性と言語的有縁性を区別しておく必要がある.前者は自然界にきこえる音を言語音に写し取る onomatopoeia の類であり,後者は派生や複合などの形態的手段によって得られる相互関係(例えば,possible と impossible の関係)である.まれな語根創成 (root_creation) の例を除いて,すべての語はいずれかの種類の有縁性によって生み出されるという事実は注目に値する.
重要なのは,有縁性は限定的でもなければ被限定的でもなく,常に自由であるという点だ.限定的でないというのは,いったん定まった signifiant と signifié の対応は不変ではなく,自由に関係を解いてよいということである.被限定的でないというのは,比喩,派生,複合,イディオム化など,どんな方法を用いても,命名したり意味づけしたりできるということである.
したがって,ほぼすべての語は様々な手段により有縁的に生み出され,そこで signifiant と signifié の対応が確定するが,確定した後には再び対応を変化させる自由を回復する.換言すれば,当初の有縁的な関係は時間とともに薄まり,忘れられ,ついには無縁的となるが,その無縁化した記号が出発点となって再び有縁化の道を歩み出す.有縁化とは意識的で非連続の個人の創作であり,無縁化とは無意識的で連続的な集団の伝播である (45) .有縁化と無縁化のあいだの永遠のサイクルは,意味論の本質にかかわる問題である.語の意味変化を有縁性という観点から図示すれば,以下のようになろう.
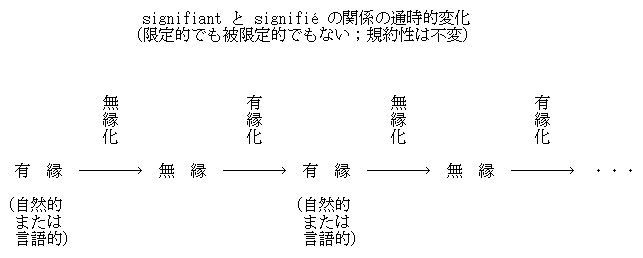
ギローにとって,ソシュールのいう恣意性とは,いつでも自由に有縁化・無縁化することができ,なおかつ常に規約的であるという記号の性質を指すものなのである.
「#1056. 言語変化は人間による積極的な採用である」 ([2012-03-18-1]) や「#1069. フォスラー学派,新言語学派,柳田 --- 話者個人の心理を重んじる言語観」 ([2012-03-31-1]) の記事でみた柳田国男の言語変化論は,上のサイクルの有縁化の部分にとりわけ注目した論ということになるだろう.
・ ピエール・ギロー 著,佐藤 信夫 訳 『意味論』 白水社〈文庫クセジュ〉,1990年.
2026 : 01 02 03 04 05 06 07 08 09 10 11 12
2025 : 01 02 03 04 05 06 07 08 09 10 11 12
2024 : 01 02 03 04 05 06 07 08 09 10 11 12
2023 : 01 02 03 04 05 06 07 08 09 10 11 12
2022 : 01 02 03 04 05 06 07 08 09 10 11 12
2021 : 01 02 03 04 05 06 07 08 09 10 11 12
2020 : 01 02 03 04 05 06 07 08 09 10 11 12
2019 : 01 02 03 04 05 06 07 08 09 10 11 12
2018 : 01 02 03 04 05 06 07 08 09 10 11 12
2017 : 01 02 03 04 05 06 07 08 09 10 11 12
2016 : 01 02 03 04 05 06 07 08 09 10 11 12
2015 : 01 02 03 04 05 06 07 08 09 10 11 12
2014 : 01 02 03 04 05 06 07 08 09 10 11 12
2013 : 01 02 03 04 05 06 07 08 09 10 11 12
2012 : 01 02 03 04 05 06 07 08 09 10 11 12
2011 : 01 02 03 04 05 06 07 08 09 10 11 12
2010 : 01 02 03 04 05 06 07 08 09 10 11 12
2009 : 01 02 03 04 05 06 07 08 09 10 11 12
最終更新時間: 2026-01-27 10:29
Powered by WinChalow1.0rc4 based on chalow