hellog〜英語史ブログ / 2012-05-12
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
2012-05-12 Sat
■ #1111. Graddol による熟達度を重視した英語話者モデル [elf][model_of_englishes][language_shift][native_speaker_problem]
1985年に Kachru によって提案された「#217. 英語話者の同心円モデル」 ([2009-11-30-1]) は,現代における英語使用を理解するためのモデルとして,広く受け入れられてきた.しかし,とりわけ21世紀が近づくにつれて,様々な批判が湧き出てきた.異論や代案は model_of_englishes の各記事で紹介してきたが,最近では Modiano による別の同心円モデルを示した ([2012-04-27-1], [2012-05-07-1]) .今回は,Kachru モデルを再解釈した Graddol の見解を紹介しよう.
Graddol (English Next 110) は,Kachru の歴史地理的な観点に基づく階層よりも,英語の熟達度に基づくモデルのほうが20世紀の英語使用の現状をよく反映していると考え,それに対応する図式を描いた(下図参照).また,熟達度の各階層は明確に区別されるというよりは,グラデーションを描く連続体だろうと考えた.Inner という用語こそ残したが,新しくここに含まれるのは「最も熟達度の高い階層」を構成する5億人ほどの英語話者ということになる.
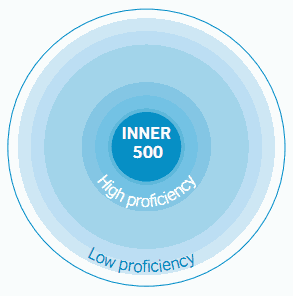
Kachru の名誉のために述べれば,彼自身も近年は Graddol のような熟達度に依拠するモデルを念頭においているようだ (Graddol, English Next 110) .
このモデルは,英語の熟達度を重視する点で Modiano の同心円モデル([2012-04-27-1]) とも比較されるが,後者はとりわけ "international English" の熟達度を問題にしている.Graddol には,"international English" に相当するものへの言及はない.また,Graddol モデルは,話者の "bilingual status" (English Next 110) という観点を,熟達度ほど重視していないが,Jenkins モデル ([2010-01-24-1]) では "bilingual status" の有無こそが肝要である.Jenkins モデルは,"the native speaker problem" を指摘しやすいモデルともいえる.
提案されてきた現代の英語使用のモデルは,それぞれ力点の置き方に差がある.そこには,英語使用の現状という以上に,提案者の英語史観や将来の英語使用への期待と希望が反映されている.したがって,私は,これらを広い意味での英語史記述であると考えている.だからこそ,様々なモデルに関心がある.
さて,Graddol といえば,前著 The Future of English? で,言語交替 (language shift) を考慮に入れた動的なモデルも提案している.そちらについては,[2010-06-15-1]の記事「#414. language shift を考慮に入れた英語話者モデル」で取り上げたので,要参照.
・ Graddol, David. English Next. British Council, 2006. Digital version available at https://www.teachingenglish.org.uk/article/english-next .
・ Graddol, David. The Future of English? The British Council, 1997. Digital version available at https://www.teachingenglish.org.uk/article/future-english .
2026 : 01 02 03 04 05 06 07 08 09 10 11 12
2025 : 01 02 03 04 05 06 07 08 09 10 11 12
2024 : 01 02 03 04 05 06 07 08 09 10 11 12
2023 : 01 02 03 04 05 06 07 08 09 10 11 12
2022 : 01 02 03 04 05 06 07 08 09 10 11 12
2021 : 01 02 03 04 05 06 07 08 09 10 11 12
2020 : 01 02 03 04 05 06 07 08 09 10 11 12
2019 : 01 02 03 04 05 06 07 08 09 10 11 12
2018 : 01 02 03 04 05 06 07 08 09 10 11 12
2017 : 01 02 03 04 05 06 07 08 09 10 11 12
2016 : 01 02 03 04 05 06 07 08 09 10 11 12
2015 : 01 02 03 04 05 06 07 08 09 10 11 12
2014 : 01 02 03 04 05 06 07 08 09 10 11 12
2013 : 01 02 03 04 05 06 07 08 09 10 11 12
2012 : 01 02 03 04 05 06 07 08 09 10 11 12
2011 : 01 02 03 04 05 06 07 08 09 10 11 12
2010 : 01 02 03 04 05 06 07 08 09 10 11 12
2009 : 01 02 03 04 05 06 07 08 09 10 11 12
最終更新時間: 2026-01-27 10:29
Powered by WinChalow1.0rc4 based on chalow