hellog〜英語史ブログ / 2012-05-04

■ #1103. GSL による Zipf's law の検証 [lexicology][statistics][frequency][zipfs_law][corpus]

　[2012-05-02-1], [2012-05-03-1]の記事で取り上げてきた Zipf's law を検証（というよりは体験）するために，General Service List (GSL) の最頻2000語余りのデータを利用して計算してみた（データファイルはこちら）．



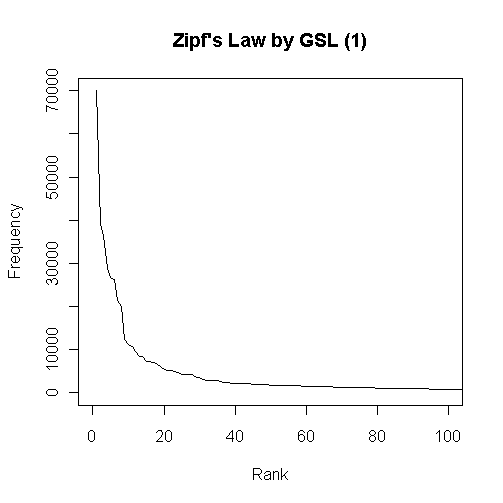
　最初のグラフは頻度順位と頻度を掛け合わせたグラフで，頻度順で100位ほどまでの語を対象とした．以下はひたすら漸減してゆくのみなので省略．累積頻度のグラフを作成するまでもなく，最頻の数十語ほどで延べ語数のほとんどを覆ってしまう様子がよくわかる．
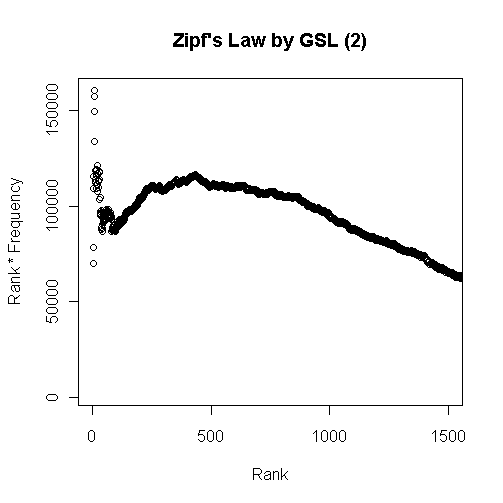
　次のグラフは，Zipf's law によると定数になるとされる頻度順位と頻度の積を縦軸にとったものである．上位数十語までは「定数」は上下に大きく揺れて安定しないが，以後1000語ぐらいまでは，緩やかな増減はあるものの，落ち着く．その後のグラフ外ではひたすら漸減を続ける．したがって，「定数」を云々できるのは大目に見ても上位1000語ぐらいまでだろう．
　これを法則と呼ぶのはあまりに外れていると考えるか，統計的傾向がよく出ているととらえるかは，観察者の見方ひとつである．Zipf's law における「定数」は「およそ定数」と解釈するのが暗黙の了解だが，「およそ」の幅がどの程度であるのかは明示されていない．また，Zipf's law が主張しているのと異なり，グラフの線は頻度をとるコーパスのサイズにも依存するようだ．

[ 固定リンク | 印刷用ページ ]