hellog〜英語史ブログ / 2009-10-24

■ #180. 古英語の人称代名詞の非対称性 [personal_pronoun][oe][inflection][paradigm]

　[2009-09-29-1]で古英語の人称代名詞の屈折表（三人称のみ）を掲げた．複雑に見えるが，この語類だけは loss of inflection の時代と呼ばれる近代英語期に至っても多くの屈折を残している．今日は，古英語の人称代名詞について，もう少し詳しく述べる．
　古英語の人称代名詞体系は，数 ( number )，格 ( case )，人称 ( person )，性 ( gender ) の四つのカテゴリーによって屈折した．以下，各カテゴリーの中身．

　数：単数，双数，複数
　格：主格，対格，属格，与格
　人称：一人称，二人称，三人称
　性：男性，女性，中性

　[2009-09-29-1]の表では「双数」 ( dual ) には触れなかったが，古英語では単数と複数の中間として，特別に「二人」を示す代名詞が存在した．だが，実際には古英語でもすでに廃れつつあった．双数を含めた人称代名詞体系の拡大版を掲げる．



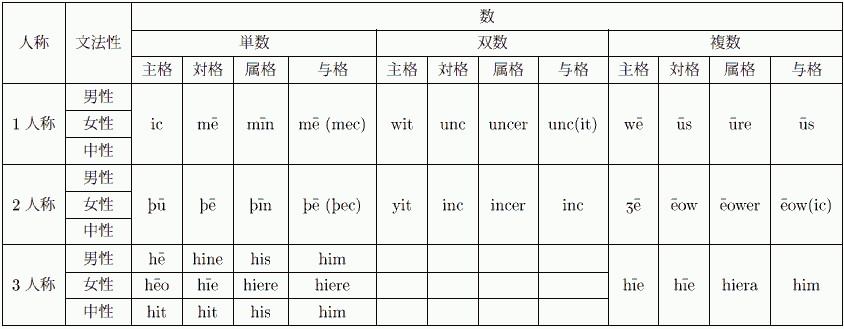
　この表から，古英語から現代英語にかけて人称代名詞体系にどんな変化が起こったかが読み取れようが，ここでは，一つ一つの具体的な変化を考えるよりも，そもそも古英語の段階から人称代名詞体系が非対称だったという事実に注目してみたい．
　本来，数，格，人称，性でフルに屈折するのであれば，3 x 4 x 3 x 3 = 108 のセルからなる表ができあがるはずだが，実際には40セルしか埋まっていない．これだけ見ても体系が不完全であることがよくわかる．各カテゴリーについて非対称的・非機能的な点を指摘しよう．

　・双数が1人称と2人称にしか存在しない
　・1人称と2人称では，対格と与格の形態的区別がない（かっこ内は古い形態を示す）
　・3人称で，his, him, hiere, hit が異なる複数の機能を果たしている
　・2人称と3人称でいう（双数と）複数は，対応する単数が複数集まったものと考えられるが，1人称の双数と複数は，対応する単数である「私」が複数集まったものではない．あくまで，私とそれ以外のものの集合である．
　・性が区別されるのは，三人称単数のみである．

　「体系」と呼びうるためには，それなりの対称性が必要である．欠陥がありつつも一応は表の形で表すことができるので，そこそこの対称性はあるということは間違いないが，期待されるほど綺麗な体系ではない．非対称性に満ちているといってよい．
　しかし，なぜそのような非対称が生じるのか．なぜカテゴリーによって区別の目が粗かったり細かかったりするのか．言語には体系を指向する力と体系を乱す力がともに働いており，その力関係は刻一刻と変化している．一定にとどまっていることがない以上，たとえある段階でより対称的になったとしても，次の段階ですぐに非対称へと逆行する．言語における体系は，ある程度の非対称をもっていることが常態なのかもしれない．

　・Görlach, Manfred. The Linguistic History of English. Basingstoke: Macmillan, 1997. 64--66.

[ 固定リンク | 印刷用ページ ]