hellog〜英語史ブログ / 2020-03-02
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
2020-03-02 Mon
■ #3962. Early Middle English Quantity Adjustment の公式 [vowel][sound_change][phonology][phonetics][meosl][homorganic_lengthening][shocc][trish][drift][emeqa]
連日の記事で Ritt に依拠しながら,後期古英語から初期中英語にかけて生じた一連の母音の量に関する変化に焦点を当ててきた.具体的には,母音の長化と短化に関する以下の4つの変化である.
・ 同器性長化 (Homorganic Lengthening; homorganic_lengthening)
・ 子音群前位置短化 (Shortening before Consonant Clusters; shocc)
・ 3音節短化 (Trisyllabic Shortening; trish)
・ 中英語開音節長化 (Middle English Open Syllable Lengthening; meosl)
従来これらの母音量変化はそれぞれ独立した現象として解釈されてきたが,昨日の記事「#3961. 3音節短化の事例」 ([2020-03-01-1]) の最後でも触れた通り,実は補完的な関係にあり,1つの駆流 (drift) ととらえる視点が提出されてきている.Ritt はこれを Early Middle English Quantity Adjustment と呼んでいる.
2つの長化については「#3958. Ritt による中英語開音節長化の公式」 ([2020-02-27-1]) で触れたように,1つの関数としてとらえることができる.改めてその公式を掲げておこう.
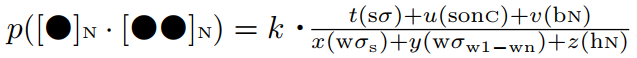
一方,2つの短化についても公式を立てることができる.短化と長化は見事に補完的であり,短化を促進させる環境では長化が抑制され,その逆もまた真である.すると,短化の公式は,上の長化の公式を逆転させればよいということになる.Ritt (95--96) の挙げている短化の公式は次の通り.
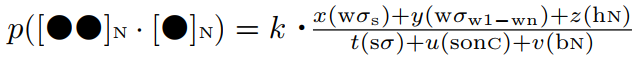
The probability of vowel shortening was proportional to
a. its height
b. syllable weight
c. the overall weight of the weak syllables in the foot
and inversely proportional to
a. the (degree of) stress on it
b. its backness
c. coda sonority
ここまで来れば,長化と短化の公式を組み合わせて,大きな1つの Early Middle English Quantity Adjustment の公式を立てることもできるだろう (Ritt 96) .
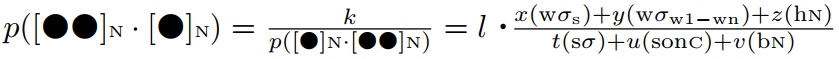
Ritt の音韻論の真骨頂は,このように音環境と音変化の関係を確率の問題に落とし込んだ点,そして一見互いに独立した変化を結びつけてみせた点にある.
・ Ritt, Nikolaus. Quantity Adjustment: Vowel Lengthening and Shortening in Early Middle English. Cambridge: CUP, 1994.
2026 : 01 02 03 04 05 06 07 08 09 10 11 12
2025 : 01 02 03 04 05 06 07 08 09 10 11 12
2024 : 01 02 03 04 05 06 07 08 09 10 11 12
2023 : 01 02 03 04 05 06 07 08 09 10 11 12
2022 : 01 02 03 04 05 06 07 08 09 10 11 12
2021 : 01 02 03 04 05 06 07 08 09 10 11 12
2020 : 01 02 03 04 05 06 07 08 09 10 11 12
2019 : 01 02 03 04 05 06 07 08 09 10 11 12
2018 : 01 02 03 04 05 06 07 08 09 10 11 12
2017 : 01 02 03 04 05 06 07 08 09 10 11 12
2016 : 01 02 03 04 05 06 07 08 09 10 11 12
2015 : 01 02 03 04 05 06 07 08 09 10 11 12
2014 : 01 02 03 04 05 06 07 08 09 10 11 12
2013 : 01 02 03 04 05 06 07 08 09 10 11 12
2012 : 01 02 03 04 05 06 07 08 09 10 11 12
2011 : 01 02 03 04 05 06 07 08 09 10 11 12
2010 : 01 02 03 04 05 06 07 08 09 10 11 12
2009 : 01 02 03 04 05 06 07 08 09 10 11 12
最終更新時間: 2026-01-27 10:29
Powered by WinChalow1.0rc4 based on chalow