hellog〜英語史ブログ / 2013-12-18
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
2013-12-18 Wed
■ #1696. 英語変種の2次元モデル [model_of_englishes][elf][variety][sociolinguistics][pidgin][creole][covert_prestige]
英語変種や英語話者を分類・整理するモデルは,「#217. 英語話者の同心円モデル」 ([2009-11-30-1]) で示した Kachru による古典的な同心円モデルを始めとして,様々なモデルを model_of_englishes の各記事で紹介してきた.今回は,Gramley (177) に示されていた,英語の社会言語学的な地位と標準性・非標準性という2つの軸を組み合わせた2次元モデルを紹介しよう.以下は,"A two-dimensional model of English showing status variation (ENL, ESL, EFL, Pidgin and Creole English) as well as GenE and traditional dialects" とラベルの貼られた図式を再現したものである.
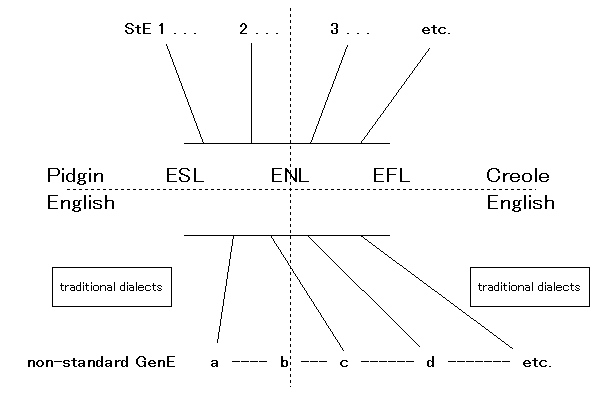
この図の水平軸には,Kachru の同心円がフラットに展開されている.ENL が中央に位置し,垂直軸との交点にあることは,この変種の威信の象徴である.その左右の隣には ESL と EFL が配され,さらに外側には Pidgin English や Creole English が置かれている.PE や CE が周辺に置かれているのは,言語的には英語から独立しているものの,歴史的,社会的には英語と関連づけられるからである.
垂直軸の表わすものについては議論の余地があるが,ここでは標準的な度合いを表わすものと考えられている.上端がもっとも標準的で,下端がもっとも非標準的ということになる.上下ともに末端は複数に分岐しており,標準英語にも非標準英語にも多数の変種があることが示されている.特に非標準変種は,General English の範囲外にあると考えられている伝統的な方言 (traditional dialects) とも近縁であることが示されている.
全体として,上に行けば行くほど顕在的権威 (overt prestige) が強く,教育と結びつけられた変種であるという解釈になる.逆に,下に行けば行くほど,潜在的権威 (covert_prestige) が強く,末広がりで互いの変異も大きい.
ピジン語やクレオール語の位置づけ,非標準変種と伝統的方言の関係などいくつかの点ではよく考えられているが,全体としては直感的にとらえにくいモデルのように思われる.例えば,Kachru の同心円モデルがフラットに水平軸に展開されていることの意味がよくわからない.垂直軸には標準・非標準というラベルを貼ることができるが,この水平軸にはどのようなラベルを貼ればよいのだろうか.また,このモデルは静的である.英語変種の収束と発散が同時進行している現代英語を記述するのには,「#414. language shift を考慮に入れた英語話者モデル」 ([2010-06-15-1]) や「#1106. Modiano の同心円モデル (2)」 ([2012-05-07-1]) のような動的なモデルがふさわしいように思われる.
・ Gramley, Stephan. The History of English: An Introduction. Abingdon: Routledge, 2012.
2026 : 01 02 03 04 05 06 07 08 09 10 11 12
2025 : 01 02 03 04 05 06 07 08 09 10 11 12
2024 : 01 02 03 04 05 06 07 08 09 10 11 12
2023 : 01 02 03 04 05 06 07 08 09 10 11 12
2022 : 01 02 03 04 05 06 07 08 09 10 11 12
2021 : 01 02 03 04 05 06 07 08 09 10 11 12
2020 : 01 02 03 04 05 06 07 08 09 10 11 12
2019 : 01 02 03 04 05 06 07 08 09 10 11 12
2018 : 01 02 03 04 05 06 07 08 09 10 11 12
2017 : 01 02 03 04 05 06 07 08 09 10 11 12
2016 : 01 02 03 04 05 06 07 08 09 10 11 12
2015 : 01 02 03 04 05 06 07 08 09 10 11 12
2014 : 01 02 03 04 05 06 07 08 09 10 11 12
2013 : 01 02 03 04 05 06 07 08 09 10 11 12
2012 : 01 02 03 04 05 06 07 08 09 10 11 12
2011 : 01 02 03 04 05 06 07 08 09 10 11 12
2010 : 01 02 03 04 05 06 07 08 09 10 11 12
2009 : 01 02 03 04 05 06 07 08 09 10 11 12
最終更新時間: 2026-01-27 10:29
Powered by WinChalow1.0rc4 based on chalow