hellog〜英語史ブログ / 2013-06-05
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
2013-06-05 Wed
■ #1500. 方言連続体 [dialect_continuum][dialect][geography][isogloss][map][terminology][language_or_dialect]
方言どうしの境界線(あるいは時に言語どうしの境界線)は,必ずしも明確に引けるとは限らない.否,多くの場合,方言線は多かれ少なかれ恣意的である.「#1317. 重要な等語線の選び方」 ([2012-12-04-1]) で述べたように,等語線 isogloss が太い束をなすところに境界線が引かれるとするのが一般的ではあるが,絶対的な基準はないといってよい.
ある旅行者が地理的に連続体をなすA村からZ村へと歩いてゆく旅を想像すると,A村の言語とB村の言語とは僅少な差しかなく,B村とC村,C村とD村も同様だろう.旅行者は,各々の言語的な差異にはほとんど気付かずに歩いて行き,ついにZ村に達する.ところが,客観的にA村とZ村の言語を比べると,明らかに大きな差異があるのである.村から村への言語差はデジタルではなくアナログであり,旅行者が体験したのは方言連続体 (dialect continuum) にほかならない.世界各地に方言連続体が存在するが,ヨーロッパだけを見ても複数の方言連続体が見られる.以下は,Romain (12) の図を参考にして作った方言連続体の地図である.
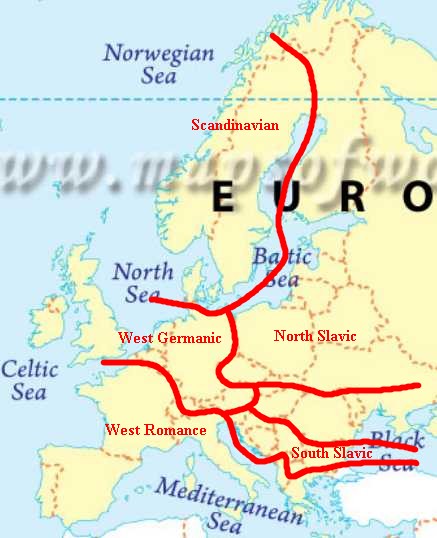
この地図は,例えばイタリア南端からフランス北部のカレーまで,あるいはアムステルダムからウィーンまで,方言連続体を旅することができるということを意味する.
方言連続体を示す地域の限界は,波線で示された国境線と一致することもあれば一致していないこともある.これは,隣り合う2つの村が国境を挟んでいるからといって,必ずしも大きく異なる言語を用いているというわけではないということを示すと同時に,場合によっては同一国内の隣り合う2つの村でも言語の断絶があり得るということを示す.
方言連続体に関しては,理論的な問題がある.A, B, C, . . . Zの村々が方言連続体を構成していると想定した場合,それぞれの村の内部では一様な言語が行なわれていると考えてよいのだろうか.あるいは,村の西端と中央と東端とではミクロな方言連続体が存在しているのだろうか.もしA村とB村がそれぞれ言語的に一様だと仮定するならば,A村は1つの方言地域 (dialect area) を構成し,B村はもう1つの方言地域を構成するということになり,A村の方言とB村の方言の間には連続体ではなく小さいながらも断絶が想定されるということにならないだろうか.方言連続体という概念と方言地域という概念はどのように関連しているのだろうか.この理論的問題は,Chambers and Trudgill の問題として,Heeringa and Nerbonne によって取り上げられている.
Chambers and Trudgill (1998) introduced an interesting puzzle, one that is related to whether dialects should be viewed as organized by areas or via a geographic continuum. They observed that a traveller walking in a straight line notices successive small changes from village to village, but seldom, if ever, observes large differences. This sounds like a justification of the continuum view . . . . (376)
いかに方言連続体が生じるか,なぜ方言が存在するのかという問題については,「#1303. なぜ方言が存在するのか --- 波状モデルによる説明」 ([2012-11-20-1]) の記事も参照.
・ Romain, Suzanne. Language in Society: An Introduction to Sociolinguistics. 2nd ed. Oxford: OUP, 2000.
・ Heeringa, Wilbert and John Nerbonne. "Dialect Areas and Dialect Continua." Language Variation and Change 13 (2001): 375--400.
・ Chambers, J. K. and Peter Trudgill. Dialectology. 2nd ed. Cambridge: CUP, 1998.
2026 : 01 02 03 04 05 06 07 08 09 10 11 12
2025 : 01 02 03 04 05 06 07 08 09 10 11 12
2024 : 01 02 03 04 05 06 07 08 09 10 11 12
2023 : 01 02 03 04 05 06 07 08 09 10 11 12
2022 : 01 02 03 04 05 06 07 08 09 10 11 12
2021 : 01 02 03 04 05 06 07 08 09 10 11 12
2020 : 01 02 03 04 05 06 07 08 09 10 11 12
2019 : 01 02 03 04 05 06 07 08 09 10 11 12
2018 : 01 02 03 04 05 06 07 08 09 10 11 12
2017 : 01 02 03 04 05 06 07 08 09 10 11 12
2016 : 01 02 03 04 05 06 07 08 09 10 11 12
2015 : 01 02 03 04 05 06 07 08 09 10 11 12
2014 : 01 02 03 04 05 06 07 08 09 10 11 12
2013 : 01 02 03 04 05 06 07 08 09 10 11 12
2012 : 01 02 03 04 05 06 07 08 09 10 11 12
2011 : 01 02 03 04 05 06 07 08 09 10 11 12
2010 : 01 02 03 04 05 06 07 08 09 10 11 12
2009 : 01 02 03 04 05 06 07 08 09 10 11 12
最終更新時間: 2026-01-27 10:29
Powered by WinChalow1.0rc4 based on chalow