hellog〜英語史ブログ / 2019-06-29
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
2019-06-29 Sat
■ #3715. 音節構造に Rhyme という単位を認める根拠 [syllable][phonetics][phonology][terminology]
「#1563. 音節構造」 ([2013-08-07-1]) で論じたように,音韻論的には英語の音節構造として「右枝分かれ構造」 (right-branching structure) を想定することが多い.図式的に表現すれば,以下のようにまず音節 (syllable = σ) が頭子音 (onset) と韻 (rhyme) に分かれ,後者がさらに核 (nucleus) と尾子音 (coda) に分かれる構造である.
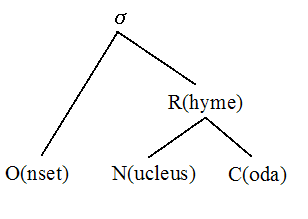
ところで,なぜこのような構造を想定するのが理論的に好都合なのだろうか.先の記事でも多少論じたが,今回は服部 (66) に従って,音声学・音韻論の観点からもう少し具体的に根拠を示そう.
英語の母音には,音節末に生起可能な開放母音と不可能な抑止母音の2種類が区別される.原則として,他の条件が同じであれば,抑止母音よりも開放母音のほうが長く発音される.また,開放母音に関しては,尾子音が後続しない場合に最も長く,次に有声尾子音が続くとき,そして無声尾子音が続くときという順序で母音の長さが短くなっていく.具体的な単語例で示せば,母音の短い順に bit < bid, beet < bead < bee と並べられることになる.
この事実を尾子音の種類に着目して言い換えれば,無声子音は有声子音よりも長く発音されるということになる.つまり,無声子音は比較的長い発音をもっているから,先行する母音はその分短く発音され,逆に有声子音は比較的短い発音をもっているから,先行する母音はその分長く発音されると解釈することができる.
このように考えると,核の母音と尾子音は長さに関して相補的・代償的な関係にあるといえる.同様の関係は頭子音と核の間には確認されないことから,上のような構造を想定するのが妥当だという結論に至るのである.
主として英語の韻文における伝統的な技巧として脚韻 (rhyme) が存在することは,それ自体では上の構造を想定する強力な根拠とはならないが,同構造が妥当であることの傍証にはなるだろう.
・ 服部 義弘 「第4章 音節・音連鎖・連続音制過程」服部 義弘(編)『音声学』朝倉日英対照言語学シリーズ 2 朝倉書店,2012年.64--83頁.
2026 : 01 02 03 04 05 06 07 08 09 10 11 12
2025 : 01 02 03 04 05 06 07 08 09 10 11 12
2024 : 01 02 03 04 05 06 07 08 09 10 11 12
2023 : 01 02 03 04 05 06 07 08 09 10 11 12
2022 : 01 02 03 04 05 06 07 08 09 10 11 12
2021 : 01 02 03 04 05 06 07 08 09 10 11 12
2020 : 01 02 03 04 05 06 07 08 09 10 11 12
2019 : 01 02 03 04 05 06 07 08 09 10 11 12
2018 : 01 02 03 04 05 06 07 08 09 10 11 12
2017 : 01 02 03 04 05 06 07 08 09 10 11 12
2016 : 01 02 03 04 05 06 07 08 09 10 11 12
2015 : 01 02 03 04 05 06 07 08 09 10 11 12
2014 : 01 02 03 04 05 06 07 08 09 10 11 12
2013 : 01 02 03 04 05 06 07 08 09 10 11 12
2012 : 01 02 03 04 05 06 07 08 09 10 11 12
2011 : 01 02 03 04 05 06 07 08 09 10 11 12
2010 : 01 02 03 04 05 06 07 08 09 10 11 12
2009 : 01 02 03 04 05 06 07 08 09 10 11 12
最終更新時間: 2026-01-27 10:29
Powered by WinChalow1.0rc4 based on chalow