hellog〜英語史ブログ / 2017-03-11
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
2017-03-11 Sat
■ #2875. 英語語彙の頻度分布の格差をジニ係数とローレンツ曲線でみる [lexicology][statistics][frequency][zipfs_law][corpus]
「#1103. GSL による Zipf's law の検証」 ([2012-05-04-1]) で,General Service List (GSL) の最頻2000語余りの語彙頻度表を用いて,zipfs_law が成立する様子を実演した.頻度順位の高い少数の語がただの高頻度語ではなく超高頻度語であること,一方でそれ以外の大多数の語がおしなべて低頻度語であるということが確認された.このことは,英語(そして,おそらくあらゆる言語)の語彙の頻度分布がきわめて不平等・不均衡であり,大きなばらつきと格差に特徴づけられていることを示すものである.
このような分布の格差を示す代表的な指標に,イタリアの経済学者ジニが所得や資産の分布の不平等を計測する指標として1936年に考案したジニ係数 (Gini's coefficient) がある.考え方は次の通りだ.X軸に沿って左から右へ最も頻度の低い語から高い語へと順に並べ,その累積頻度のシェアをY軸方向に取っていく.この点をつなげると,何らかの形の右肩上がりの曲線となる.これをローレンツ曲線 (Lorenz curve) という.すべての語が同頻度で現われるときにはローレンツ曲線は45度の右肩上がりの直線となり「完全平等」を示す.逆に,極端な例として,1つの語のみが生起頻度のすべてを占有し,他のすべての語が頻度ゼロの場合に「完全不平等」となり,ローレンツ曲線は左右逆L字型となる.普通は,ローレンツ曲線は,45度の右肩上がりの線の下部に,三日月形の弧として描かれる.ジニ係数は,三日月の面積と,45度の右肩上がりの線を直角の対辺とする直角二等辺三角形の比率として表現される.したがって,値0が完全平等,値1が完全不平等ということになる.
さて,GSL のデータファイルで計算した結果,ジニ係数は0.812と出た.ローレンツ曲線を描くと,以下のようになる.
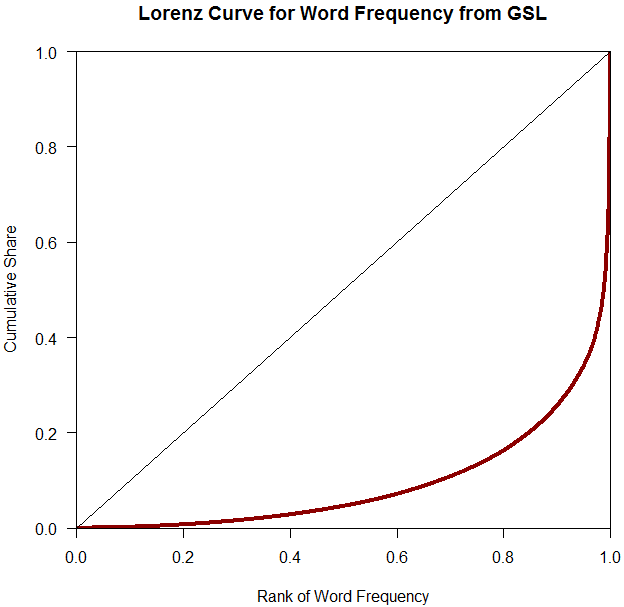
明らかに不平等な分布といえる.ちなみに,GSL よりも巨大なコーパスの語彙頻度表を使うと,さらにジニ係数は上がる(例えば,1790万語からなるコーパス「#1424. CELEX2」 ([2013-03-21-1]) に基づいた計算では,0.950 というすさまじい値が出た!).
参考までに,吉川 (122) に拠って2010年の諸国の所得格差を示すジニ係数をいくつか挙げると,日本が 0.336,アメリカが 0.380,チリが 0.510,アイスランドが 0.246 である.語彙の社会が極めて不平等な社会であることが分かるだろう.
・ 吉川 洋 『人口と日本経済』 中央公論新社〈中公新書〉,2016年.
2026 : 01 02 03 04 05 06 07 08 09 10 11 12
2025 : 01 02 03 04 05 06 07 08 09 10 11 12
2024 : 01 02 03 04 05 06 07 08 09 10 11 12
2023 : 01 02 03 04 05 06 07 08 09 10 11 12
2022 : 01 02 03 04 05 06 07 08 09 10 11 12
2021 : 01 02 03 04 05 06 07 08 09 10 11 12
2020 : 01 02 03 04 05 06 07 08 09 10 11 12
2019 : 01 02 03 04 05 06 07 08 09 10 11 12
2018 : 01 02 03 04 05 06 07 08 09 10 11 12
2017 : 01 02 03 04 05 06 07 08 09 10 11 12
2016 : 01 02 03 04 05 06 07 08 09 10 11 12
2015 : 01 02 03 04 05 06 07 08 09 10 11 12
2014 : 01 02 03 04 05 06 07 08 09 10 11 12
2013 : 01 02 03 04 05 06 07 08 09 10 11 12
2012 : 01 02 03 04 05 06 07 08 09 10 11 12
2011 : 01 02 03 04 05 06 07 08 09 10 11 12
2010 : 01 02 03 04 05 06 07 08 09 10 11 12
2009 : 01 02 03 04 05 06 07 08 09 10 11 12
最終更新時間: 2026-01-27 10:29
Powered by WinChalow1.0rc4 based on chalow