hellog〜英語史ブログ / 2017-02-09
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
2017-02-09 Thu
■ #2845. 言語学の諸分野をイェルムスレウの認識論から見ると [linguistics][diachrony][glossematics][linguistics][history_of_linguistics][semiotics][sign]
セミル・バディル(著)『ソシュールの最大の後継者 イェルムスレウ』を読んで,難解とされる言理学 (glossematics) を概観した(「#1074. Hjelmslev の言理学」 ([2012-04-05-1]) も参照).
イェルムスレウの記号学的認識論の中心に,外示記号,共示記号,メタ記号の区別がある.外示記号はいわば通常の記号を指す.共示記号は,表現部それ自体が記号であるような記号を指す.そして,メタ記号は,内容部それ自体が記号であるような記号を指す.この基本的な対立に,範列的 (paradigmatic) と連辞的 (syntagmatic) というソシュール以来よく知られた対立が組み込まれ,1つの認識論が構成される.
このイェルムスレウの認識論に立って,既存の言語学諸分野の位置づけを整理すると,以下の表のようになるだろう(バディル,p. 205).
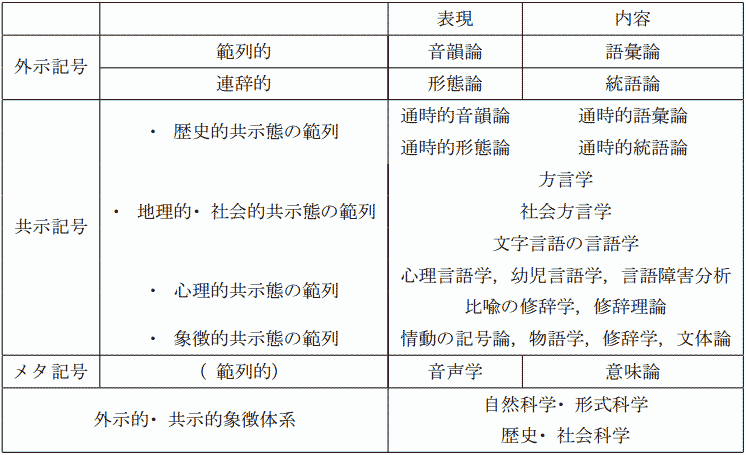
留意すべきは,既存の分野名のもとで研究されてきた内容が,そのままイェルムスレウ的な認識論における同名の分野のもとで扱われるとは限らないことだ.例えば,外示記号の表現の連辞を扱う「形態論」は,およそ伝統的な「形態論」で扱されてきた分野を覆うと考えてよいが,音素の統語的変異などを扱う問題も含むという点で少し守備安易が異なる.
この表の個別部分について見ると,特に興味深いのは,「通時」あるいは「歴史」が共示記号の範列の変異に関わる次元の1つとしてとらえられている点である.それと同列に別の次元を構成しているのは「地理」「社会」「心理」「象徴」などである.ここでは,「通時」がとりたてて「共時」に対立するものとして立てられているわけではなく,むしろ「地理」「社会」「心理」「象徴」などとの並列性が強調されている.
バディル (207--08) では,この共時・通時の再解釈について,次のように述べられている.
このように提示された言語分析は,共時的な分析だと見なされる必要はない.通時的分析をも「包含する」からである.この包含関係は,共時態と通時態の対立を定式化し直す必要性を意味する.つまり,通時態とは,共時態の「層」が重なり合って作られるものではない.形式的理論において関与的なのは,むしろその逆である.外示記号の「考古学的」な分析を実行することが可能なのである.したがって,歴史的特徴は,他の個別化をもたらす観点の中で,外示記号の作る一つの次元だということになる.
共時的言語学が圧倒的に優勢な現在,言語学のなかに通時態を復活させようとすることは簡単な試みではないが,イェルムスレウの認識論は1つのヒントになりそうだ.
言語学の諸部門の整理という話題については,「#378. 語用論は言語理論の基本構成部門か否か」 ([2010-05-10-1]),「#1110. Guiraud による言語学の構成部門」 ([2012-05-11-1]),「#1726. 「形態」の紛らわしさと Ullmann による言語学の構成部門」 ([2014-01-17-1]) も参照.
・ セミル・バディル(著),町田 健(訳) 『ソシュールの最大の後継者 イェルムスレウ』 大修館,2007年.
2026 : 01 02 03 04 05 06 07 08 09 10 11 12
2025 : 01 02 03 04 05 06 07 08 09 10 11 12
2024 : 01 02 03 04 05 06 07 08 09 10 11 12
2023 : 01 02 03 04 05 06 07 08 09 10 11 12
2022 : 01 02 03 04 05 06 07 08 09 10 11 12
2021 : 01 02 03 04 05 06 07 08 09 10 11 12
2020 : 01 02 03 04 05 06 07 08 09 10 11 12
2019 : 01 02 03 04 05 06 07 08 09 10 11 12
2018 : 01 02 03 04 05 06 07 08 09 10 11 12
2017 : 01 02 03 04 05 06 07 08 09 10 11 12
2016 : 01 02 03 04 05 06 07 08 09 10 11 12
2015 : 01 02 03 04 05 06 07 08 09 10 11 12
2014 : 01 02 03 04 05 06 07 08 09 10 11 12
2013 : 01 02 03 04 05 06 07 08 09 10 11 12
2012 : 01 02 03 04 05 06 07 08 09 10 11 12
2011 : 01 02 03 04 05 06 07 08 09 10 11 12
2010 : 01 02 03 04 05 06 07 08 09 10 11 12
2009 : 01 02 03 04 05 06 07 08 09 10 11 12
最終更新時間: 2026-01-27 10:29
Powered by WinChalow1.0rc4 based on chalow