hellog〜英語史ブログ / 2014-09-18

■ #1970. 多義性と頻度の相関関係 [polysemy][zipfs_law][information_theory][frequency][statistics]

　基本語彙と呼ばれるものの多面的な性質について「#1960. 英語語彙のピラミッド構造」 ([2014-09-08-1]) で触れた．基本語彙とは，日常的で頻度が高く，早期に習得され，変化しにくく，意味・用法が多岐にわたるなどの特徴をもつ．関連する話題は，「#308. 現代英語の最頻英単語リスト」 ([2010-03-01-1])，「#1089. 情報理論と言語の余剰性」 ([2012-04-20-1])，「#1091. 言語の余剰性，頻度，費用」 ([2012-04-22-1])，「#1101. Zipf's law」 ([2012-05-02-1])，「#1874. 高頻度語の語義の保守性」 ([2014-06-14-1])，「#1961. 基本レベル範疇」 ([2014-09-09-1])，「#1965. 普遍的な語彙素」 ([2014-09-13-1]) その他の記事でいろいろと扱ってきた．
　今回は，この問題と関連して，高頻度語は多義的であるという命題について考えてみたい．頻度の高い語ほど語義を多くもち，頻度の低い語は語義を多くもたないということは言語使用の事実に照らして実証されるだろうか．また，理論的にいかに説明されるだろうか．Zipf's law で知られる Zipf は，情報理論の立場からこの課題に挑んだ．
　Zipf は，E. L. Thorndike の英語最頻20,000語と Thorndike-Century Senior Dictionary に基づき，語の頻度と語義数の相関関係を探った．この辞書は，古語や廃語などの特殊な register をもつ語義は掲載しておらず，一般的に用いられる語義のみを掲載している．丹念に調査した結果，ある頻度域と，そこに属する語が示す平均語義数との間に，明らかな相関関係が見いだされた．以下は，Zipf (253) に示されているグラフを再現したものである．両軸ともに対数軸であり，X軸は頻度順位を，Y軸は頻度域の平均語義数を表わす．



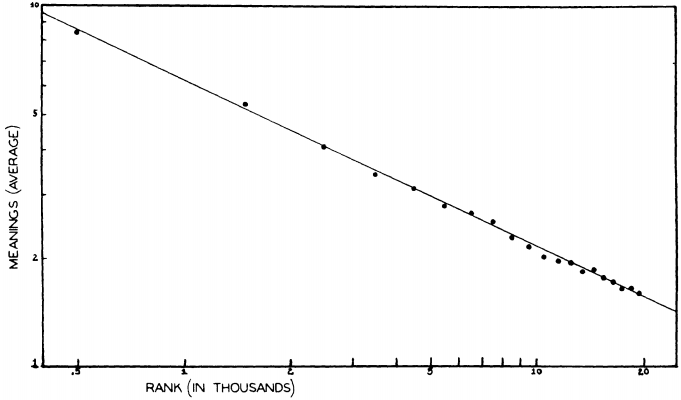
　傾きはほぼ0.5に等しく，これは話者の発話と聴者の聴解にかかる費用に関する理論の予測と符合するという．その理論の数学的裏付けは私の理解を超えるので解説できないが，Zipf は結論として語の語義数と頻度（順位）の関係について次のように定式化した (Zipf 255) ．

. . . different meanings of a word will tend to be equal to the square root of its relative frequencies (with the possible exception of the few dozen most frequent words)

　背景には，多義の定義やある語の語義をいかに区分するかといった意味論の側で問うべき問題もおおいにあるが，示唆に富んだ結論である．関連して，「#1091. 言語の余剰性，頻度，費用」 ([2012-04-22-1]) や zipfs_law の各記事も参照されたい．

　・ Zipf, G. K. "The Meaning-Frequency Relationship of Words." Journal of General Psychology 33 (1945): 251--66.

[ 固定リンク | 印刷用ページ ]