hellog〜英語史ブログ / 2013-09-09
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
2013-09-09 Mon
■ #1596. 分極の仮説 [lexical_diffusion][language_change][speed_of_change][generative_grammar][negative][syntax][do-periphrasis][schedule_of_language_change]
標題は英語で "polarization hypothesis" と呼ばれる.児馬先生の著書で初めて知ったものである.昨日の記事「#1572. なぜ言語変化はS字曲線を描くと考えられるのか」 ([2013-08-16-1]) および「#1569. 語彙拡散のS字曲線への批判 (2)」 ([2013-08-13-1]) などで言語変化の進行パターンについて議論してきたが,S字曲線と分極の仮説は親和性が高い.
分極の仮説は,生成文法やそれに基づく言語習得の枠組みからみた言語変化の進行に関する仮説である.それによると,文法規則には大規則 (major rule) と小規則 (minor rule) が区別されるという.大規則は,ある範疇の大部分の項目について適用される規則であり,少数の例外的な項目(典型的には語彙項目)には例外であるという印がつけられており,個別に処理される.一方,小規則は,少数の印をつけられた項目にのみ適用される規則であり,それ以外の大多数の項目には適用されない.両者の差異を際立たせて言い換えれば,大規則には原則として適用されるが少数の適用されない例外があり,小規則には原則として適用されないが少数の適用される例外がある,ということになる.共通点は,例外項目の数が少ないことである.分極の仮説が予想するのは,言語の規則は例外項目の少ない大規則か小規則のいずれかであり,例外項目の多い「中規則」はありえないということだ.習得の観点からも,例外のあまりに多い中規則(もはや規則と呼べないかもしれない)が非効率的であることは明らかであり,分極の仮説に合理性はある.
分極の仮説と言語変化との関係を示すのに,迂言的 do ( do-periphrasis ) による否定構造の発達を挙げよう.「#486. 迂言的 do の発達」 ([2010-08-26-1]) ほかの記事で触れた話題だが,古英語や中英語では否定構文を作るには定動詞の後に not などの否定辞を置くだけで済んだ(否定辞配置,neg-placement)が,初期近代英語で do による否定構造が発達してきた.do 否定への移行の過程についてよく知られているのは,know, doubt, care など少数の動詞はこの移行に対して最後まで抵抗し,I know not などの構造を続けていたことである.
さて,古英語や中英語では否定辞配置が大規則だったが,近代英語では do 否定に置き換えられ,一部の動詞を例外としてもつ小規則へと変わった.do 否定の観点からみれば,発達し始めた16世紀には,少数の動詞が関与するにすぎない小規則だったが,17世紀後半には少数の例外をもつ大規則へと変わった.否定辞配置の衰退と do 否定の発達をグラフに描くと,中間段階に著しく急速な変化を示す(逆)S字曲線となる.
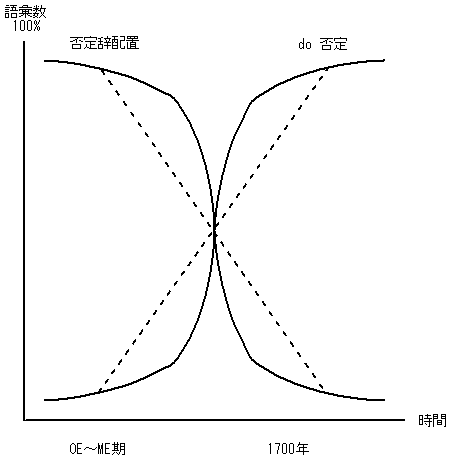
語彙拡散と分極の仮説は,理論の出所がまるで異なるにもかかわらず,S字曲線という点で一致を見るというのがおもしろい.
合わせて,分極の仮説の関連論文として園田の「分極の仮説と助動詞doの発達の一側面」を読んだ.園田は,分極の仮説を,生成理論の応用として通時的な問題を扱う際の補助理論と位置づけている.
・ 児馬 修 『ファンダメンタル英語史』 ひつじ書房,1996年.111--12頁.
・ 園田 勝英 「分極の仮説と助動詞doの発達の一側面」『The Northern Review (北海道大学)』,第12巻,1984年,47--57頁.
2026 : 01 02 03 04 05 06 07 08 09 10 11 12
2025 : 01 02 03 04 05 06 07 08 09 10 11 12
2024 : 01 02 03 04 05 06 07 08 09 10 11 12
2023 : 01 02 03 04 05 06 07 08 09 10 11 12
2022 : 01 02 03 04 05 06 07 08 09 10 11 12
2021 : 01 02 03 04 05 06 07 08 09 10 11 12
2020 : 01 02 03 04 05 06 07 08 09 10 11 12
2019 : 01 02 03 04 05 06 07 08 09 10 11 12
2018 : 01 02 03 04 05 06 07 08 09 10 11 12
2017 : 01 02 03 04 05 06 07 08 09 10 11 12
2016 : 01 02 03 04 05 06 07 08 09 10 11 12
2015 : 01 02 03 04 05 06 07 08 09 10 11 12
2014 : 01 02 03 04 05 06 07 08 09 10 11 12
2013 : 01 02 03 04 05 06 07 08 09 10 11 12
2012 : 01 02 03 04 05 06 07 08 09 10 11 12
2011 : 01 02 03 04 05 06 07 08 09 10 11 12
2010 : 01 02 03 04 05 06 07 08 09 10 11 12
2009 : 01 02 03 04 05 06 07 08 09 10 11 12
最終更新時間: 2026-01-27 10:29
Powered by WinChalow1.0rc4 based on chalow