hellog〜英語史ブログ / 2013-08-07
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
2013-08-07 Wed
■ #1563. 音節構造 [syllable][phonetics][phonology][metrical_phonology][terminology]
昨日の記事「#1562. 韻律音韻論からみる yod-dropping」 ([2013-08-06-1]) で,説明抜きで音節構造 (syllable structure) の分析を示したが,今日は Hogg and McCully (35--38) に拠って,音節構造の教科書的な概説を施したい.以下では,grind /graind/ という1音節語の音節構造を例に取る.
最も直感的な分析方法は,音節を構成する各分節音をフラットに並べる下図の (1) の方法である.ただし,音声学的にも音韻論的にも,母音と子音とを区別することは前提としておいてよいと思われるので,その標示は与えてある.
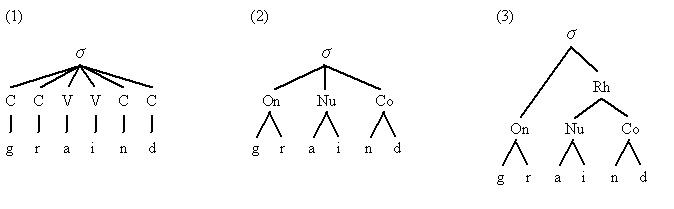
(1) を一見して明らかなように,子音は子音どうしの結合をなし,母音は母音どうしの結合をなすのが通常である.したがって,それぞれをグループ化して音節内での位置に応じてラベルをつけることは自然である.音節の始まりを担当する子音群を Onset,本体を占める母音群を Nucleus,終わりを担当する子音群を Coda と分けることが一般的に行なわれている.これが,(2) の分析である.
この段階でも有効な音節構造の分析はできるが,さらに階層化を進めると,理論上,便利である.(3) のように Nucleus と Coda をまとめる Rhyme を設定し,Onset に対応させるという分析が広く受け入れられている.
では,(3) のような一見すると複雑な階層化がなぜ理論的に有意味なのだろうか.1つは,Onset には独自の制限がかかっているということがある.英語では /graind/ という音連続は許されるが,例えば */pfraind/ は許されない.これは,Onset /pfr/ にかかっている子音連続の制限ゆえであり,Onset より右の部分の構造からは独立した理由によるものである.同様に,brim, bread, bran, brock, brunt と *bnim, *bnead, *bnan, *bnock, *bnunt を比較すれば,問題は Onset が /br/ か */bn/ かにかかっているのであり,その後の部分は全体の可否に影響していないことがわかるだろう.また,Rhyme という語そのものが示すとおり,脚韻の伝統により,この単位が直感的にもまとまりをなすものだという認識は強い.
さらに,Rhyme (あるいはそれより下のレベル)の分岐の仕方により,多くの音韻過程や強勢が記述できるという利点がある.分岐していれば重い音節 (heavy syllable) であると言われ,分岐していなければ軽い音節 (light syllable) であると言われる.Nucleus と Coda の構造に別々に言及せずとも,Rhyme 以下の構造として一括して言及できるので,Rhyme というレベルの設定は説明の経済性に資する.
以上の理由で,Onset に対して Rhyme を区別する合理性はあるといえる.しかし,Rhyme 以下を Nucleus と Coda へ区分せずに,音をフラットに横並びにする音韻論など,(3) の変種といえるものもあることに注意したい.いずれも合理的に音韻や韻律の分析を可能にするための仮説であり,道具立てである.
・ Hogg, Richard and C. B. McCully. Metrical Phonology: A Coursebook. Cambridge: CUP, 1987.
2026 : 01 02 03 04 05 06 07 08 09 10 11 12
2025 : 01 02 03 04 05 06 07 08 09 10 11 12
2024 : 01 02 03 04 05 06 07 08 09 10 11 12
2023 : 01 02 03 04 05 06 07 08 09 10 11 12
2022 : 01 02 03 04 05 06 07 08 09 10 11 12
2021 : 01 02 03 04 05 06 07 08 09 10 11 12
2020 : 01 02 03 04 05 06 07 08 09 10 11 12
2019 : 01 02 03 04 05 06 07 08 09 10 11 12
2018 : 01 02 03 04 05 06 07 08 09 10 11 12
2017 : 01 02 03 04 05 06 07 08 09 10 11 12
2016 : 01 02 03 04 05 06 07 08 09 10 11 12
2015 : 01 02 03 04 05 06 07 08 09 10 11 12
2014 : 01 02 03 04 05 06 07 08 09 10 11 12
2013 : 01 02 03 04 05 06 07 08 09 10 11 12
2012 : 01 02 03 04 05 06 07 08 09 10 11 12
2011 : 01 02 03 04 05 06 07 08 09 10 11 12
2010 : 01 02 03 04 05 06 07 08 09 10 11 12
2009 : 01 02 03 04 05 06 07 08 09 10 11 12
最終更新時間: 2026-01-27 10:29
Powered by WinChalow1.0rc4 based on chalow