hellog〜英語史ブログ / 2012-03-07
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
2012-03-07 Wed
■ #1045. 柳田国男の方言周圏論 [wave_theory][dialect][geography][isogloss]
「#999. 言語変化の波状説」 ([2012-01-21-1]) や「#1000. 古語は辺境に残る」 ([2012-01-22-1]) で波状説や言語地理学 (linguistic geography) について触れた.日本における同様の説としては,柳田国男 (1875--1962) が『蝸牛考』 (1930) にて提唱した方言周圏論が有名である.
『蝸牛考』は我が国における言語地理学の最初の論考であり,そこで示された方言周圏論は,1872年に Johannes Schmidt (1843--1901) の発表した the wave theory (Wellentheorie) の日本版といってよい.柳田が Schmidt の説を知っていたかどうかは明らかでないが,フランスの言語地理学については学んでいたようであり,発想の点で間接的に影響を受けていたということは考えられる.
柳田は,語によって方言ごとに異形の種類はまちまちであることを取り上げ,これを各語の方言量と呼んだ (21) .とりわけ方言量の多い語として,柳田が方言調査のために選んだのが「蝸牛」である.まず,京都を中心とする近畿地方で「デデムシ」の分布が確認される.そのすぐ東側と西側,中部や中国では「マイマイ」が分布しており,さらにその外側,関東や四国では「カタツムリ」の地域が広がっている.その外縁を形成する東北と九州では「ツブリ」が,そのまた外側に位置する東北北部と九州西部では「ナメクジ」の地域が見られる.蝸牛の呼称の等語線 (isogloss) は,細かくみれば,多くの言語項目の方言線と同様に錯綜しているが,図式化すれば以下のようになる(波線で表わした長方形は日本列島に相当).
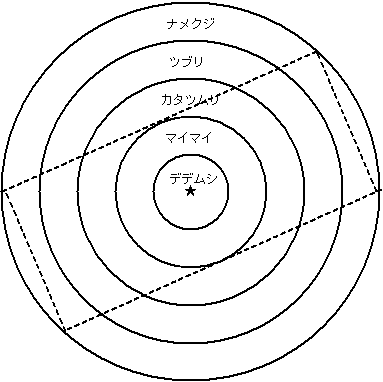
ここから推定されるのは,蝸牛を表わす語が,時期を違えて次々と京都付近で生まれ,各々が同心円状に外側に広がっていったという過程である.逆からみると,最も外側に分布する語が最古層を形成し,内側にゆくにしたがって新しい層となり,京都にいたって最新層に出会う.地層を観察すればかつての地質活動を推定できるのと同様に,方言分布を観察すればかつての言語項目の拡散の仕方を推定できることを,柳田は蝸牛語によって実証的に示したのである.なお,「ナメクジ」のさらに古層として周縁部に貝類の総称としての「ミナ」が分布しているというのも興味深い(柳田,pp. 149--50).
蝸牛語の実証はみごとだが,後に柳田自身も述べている通り,方言周圏論は方言分布の解釈の1つにすぎない.語彙についてはある程度うまく説明することができても,音韻やアクセントの分布では,むしろ中心こそ保守的な特徴を保つとされ,方言周圏論は適用できない.語彙についてさえ,各地で独立に新形態が生まれる多元発生説も唱えられている.また,新形態の拡大は,必ずしも地を這って進むとは限らないという考えもある.
方言周圏論あるいは波状説について日本語と英語とで異なっている点は,日本語では,近世前期までは,主要な言語変化は京都を中心とすると考えておよそ間違いないが,英語では必ずしもロンドンを中心とする革新ばかりではなかったという点だ.ロンドンを中心とする南イングランドが言語革新の発信地となって,それが同心円状に各地へと伝播してゆく過程は,確かにある.[2010-07-23-1]の記事「#452. イングランド英語の諸方言における r」で紹介した,18世紀後半の postvocalic r の消失が代表例だ.一方で,[2011-11-24-1]の記事「#941. 中英語の言語変化はなぜ北から南へ伝播したのか」で取り上げたイングランド北部や東部を発信地とする言語変化も多く確認される.したがって,方言周圏論の立場から見ると,イングランドは南北両方から発信された同心円が錯綜し,複合的な方言状況を呈しているということになる.
・ 柳田 国男 『蝸牛考』 岩波書店,1980年.
2026 : 01 02 03 04 05 06 07 08 09 10 11 12
2025 : 01 02 03 04 05 06 07 08 09 10 11 12
2024 : 01 02 03 04 05 06 07 08 09 10 11 12
2023 : 01 02 03 04 05 06 07 08 09 10 11 12
2022 : 01 02 03 04 05 06 07 08 09 10 11 12
2021 : 01 02 03 04 05 06 07 08 09 10 11 12
2020 : 01 02 03 04 05 06 07 08 09 10 11 12
2019 : 01 02 03 04 05 06 07 08 09 10 11 12
2018 : 01 02 03 04 05 06 07 08 09 10 11 12
2017 : 01 02 03 04 05 06 07 08 09 10 11 12
2016 : 01 02 03 04 05 06 07 08 09 10 11 12
2015 : 01 02 03 04 05 06 07 08 09 10 11 12
2014 : 01 02 03 04 05 06 07 08 09 10 11 12
2013 : 01 02 03 04 05 06 07 08 09 10 11 12
2012 : 01 02 03 04 05 06 07 08 09 10 11 12
2011 : 01 02 03 04 05 06 07 08 09 10 11 12
2010 : 01 02 03 04 05 06 07 08 09 10 11 12
2009 : 01 02 03 04 05 06 07 08 09 10 11 12
最終更新時間: 2026-01-27 10:29
Powered by WinChalow1.0rc4 based on chalow