hellog〜英語史ブログ / 2011-02-28
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
2011-02-28 Mon
■ #672. 構造主義的にみる中英語ロマンス [literature][romance][formula]
[2011-02-26-1], [2011-02-27-1]の記事で参照した Wittig は,中英語ロマンスの formula を機能的な単位として位置づけた研究者である.Wittig の議論には構造主義の視点が色濃く反映されており,それは特に次の2点において見られる.
1つは,formula を "a kind of mental template, in the mind of the poet, a pattern-making device which generates a series of derivative forms" (Wittig 29) とみなしている点である.この考えによると,formula とは統合関係 ( syntagm ) を表わす「型」のことであり,そこに選択関係 ( paradigm ) にある交替可能な語句群から1つを選んで流し込んでゆくことによってある表現が実現されるとする.例えば al thus in boke as as we rede という決まり文句は,以下の「型」の各スロットに適当な語句を選択して当てはめていった結果であると考える.
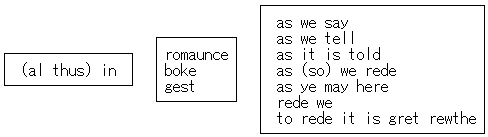
もう1つすぐれて構造主義的なのは,上記のような統語レベルの型を "syntagmeme" と名付けてロマンスの構造をなす最小単位と位置づけたあとで,「交替可能な選択肢の中からの選択」という考え方をより大きな単位へと拡張してゆく点である.例えば,ロマンスには「主人公の父の死」という場面がある.この場面を構成するのは「悪者による殺害の企み」「父の登場」「敵の挑戦」「敵との戦い」「死」という一連の出来事であり,それぞれの出来事の単位は "motifeme" と呼ばれる.各 motifeme には様々な variation が用意されており,また motifeme 間の順番は決まっている.型に流し込むかのように場面が構成されてゆく.次に,「主人公の父の死」という場面それ自体がより大きな構成単位 "type-scene" となり,「主人公の追放」というもう1つの type-scene と合わさって,さらに大きな構成単位 "type-episode" となる.いずれの規模の単位においても「交替可能な選択肢の中からの選択」という同一原則が適用されており,小さい単位の積み重ねにより最終的な物語が構成されるという意味で,きわめて構造主義的な考え方といえる.
Wittig は,"Dame," he said のような単純な formula の分析から始め,より大きな単位へと分析へと積み上げてゆき,結論として中英語ロマンスに共通する2対の type-episode 連鎖を突き止めた."love-marriage" 連鎖と "separation-restoration" 連鎖である.Wittig (177) は,中英語ロマンスの形式上の定義はこの2対の連鎖が組み合わさっているということであると言い切る.
中英語ロマンスでは,love と marriage の間に必ず困難が伴い,separation (追放によるアイデンティティの喪失)と restoration (その回復)にも苦難が付随する.2対の連鎖こそが中英語ロマンスの主要な "generating forces" であり,深層構造から,鋳型へ内容物を注入しつつ,表層構造を産出してゆく原動力なのである.
最後に,Wittig の議論は壮大な speculation へと及ぶ.中英語ロマンスの聴衆の関心の根底に love-marriage と separation-restoration があったと仮定すると,それはなぜなのか.その答えの1つとして,love-marriage が象徴する女系家族制と separation-restoration が象徴する男系家族制との融和が,かれらの大きな関心事だったからではないか.
formula の言語的分析から中世イングランドの家族観へと展開する Wittig の議論を読んで,構造主義というのは,小さな部品を1つの原理で組み合わせて大きな機械を作りあげることなのかと学んだ.
・ Wittig, Susan. Stylistic and Narrative Structures in the Middle English Romances. Austin and London: U of Texas P, 1978.
2026 : 01 02 03 04 05 06 07 08 09 10 11 12
2025 : 01 02 03 04 05 06 07 08 09 10 11 12
2024 : 01 02 03 04 05 06 07 08 09 10 11 12
2023 : 01 02 03 04 05 06 07 08 09 10 11 12
2022 : 01 02 03 04 05 06 07 08 09 10 11 12
2021 : 01 02 03 04 05 06 07 08 09 10 11 12
2020 : 01 02 03 04 05 06 07 08 09 10 11 12
2019 : 01 02 03 04 05 06 07 08 09 10 11 12
2018 : 01 02 03 04 05 06 07 08 09 10 11 12
2017 : 01 02 03 04 05 06 07 08 09 10 11 12
2016 : 01 02 03 04 05 06 07 08 09 10 11 12
2015 : 01 02 03 04 05 06 07 08 09 10 11 12
2014 : 01 02 03 04 05 06 07 08 09 10 11 12
2013 : 01 02 03 04 05 06 07 08 09 10 11 12
2012 : 01 02 03 04 05 06 07 08 09 10 11 12
2011 : 01 02 03 04 05 06 07 08 09 10 11 12
2010 : 01 02 03 04 05 06 07 08 09 10 11 12
2009 : 01 02 03 04 05 06 07 08 09 10 11 12
最終更新時間: 2026-01-19 11:07
Powered by WinChalow1.0rc4 based on chalow