hellog〜英語史ブログ / 2020-12-10
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
2020-12-10 Thu
■ #4245. 頻度と漸近双曲線 (A-curve) [lexical_diffusion][zipfs_law][frequency][statistics][language_change][uniformitarian_principle]
variationist の立場を高度に押し進めた言語(変化)観を提案する,Kretzschmar and Tamasi の論考を読んだ."A-curve", "asymptotic hyperbolic distribution", "power law", "S-curve" などの用語が連発し思わず身構えてしまう論文だが,言わんとしていることは Zipf's Law (cf. zipfs_law) の発展版のように思われる.低頻度の言語項は多く,高頻度の言語項は少ないということだ.
ある英語コーパスにおいて,1度しか現われない語は相当数ある.一方,the, of, have などは超高頻度で現われるが,主として機能語であり種類数でいえば相当に限定される.例えば,1回しか現われない語 ( x = 1 ) は1000個 ( y = 1000 ) あるが,1000回も現われる語 ( x = 1000 ) は the の1語しかない ( y = 1 ) とすると,これを座標上にプロットしてみれば第1象限の左上と右下に点が打たれることになる.この2点を両端として,その間の点を次々と埋めていくと,y = 1/x で表わせるような漸近双曲線 (asymptotic hyperbolic curve) の片割れに近づくだろう.これを Kretzschmar and Tamasi は "A-curve" と呼んでおり,背後にある法則を "power law" (べき乗則)と呼んでいる.後者は "few realizations that occur very frequently and many realizations that occur infrequently" (384) ということである.
Kretzschmar and Tamasi は,アメリカ方言における訛語や調音の variants を調査し,各種の変異形について頻度の分布を取った.結果として,いずれのケースについても "A-curve" が観察されることを示した.
また,Kretzschmar and Tamasi は,語彙拡散 (lexical_diffusion) との関連でしばしば言及される "S-curve" と,彼らの "A-curve" との関係についても議論している.同一の言語変化を異なる軸に着目してプロットすると "S-curve" にも "A-curve" にもなり,両者は矛盾しないどころか,親和性が高いという.
私の拙い言葉使いでは上手く解説することができないのだが,言語体系や言語変化を徹底的に variationist に眺めようとすると,このような言語観あるいは言語理論になるのかと感心した.Kretzschmar and Tamasi (394) より,とりわけ重要と思われる箇所を引用する.
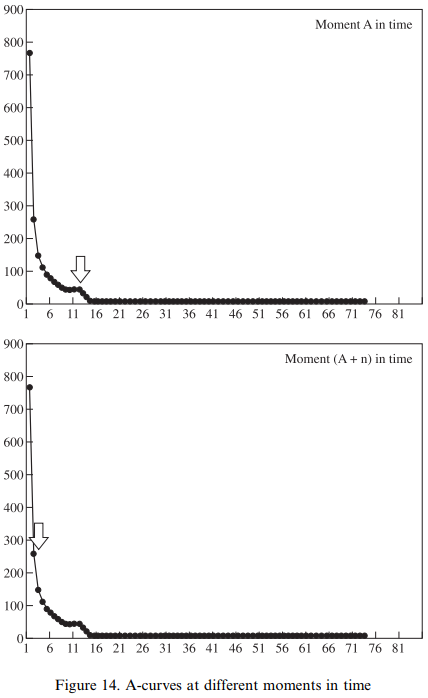
Our second observation, about the distribution of variants according to Zipf's Law, has the strongest set of implications for historical study of language. If we take the A-curve as the model for the frequency distribution of variants for any linguistic feature of interest to us at any moment in time, then we should expect that any particular variant of interest to us will have a particular rank along the A-curve. Therefore, one of the things that we should try to do for any given moment in time is to determine the place of our variant of interest on the curve; we need to know whether it is the most frequent variant in the set of possible realizations (at the top of the curve), or an infrequent variant (in the tail of the curve). Then, for any subsequent moment in time, we can again try to determine the location of our variant of interest along the curve, and so try to make a statement about whether the location of the variant has changed in the intervening time (see Figure 14). Since we hypothesize that an A-curve will exist for every feature at any moment in time (i.e., that language will not suddenly become invariant), we can define the notion "linguistic change" itself as the change in the location of the target variant at different heights along the curve. If a particular variant occurs at a higher place on the curve than it did before, it has become more frequent and so we can say that the direction of change for that variant is positive; if a variant occurs at a lower place on the curve than it did before, it has become less frequent and the direction of change is negative.
・ Kretzschmar, Jr.,William A and Susan Tamasi. "Distributional Foundations for a Theory of Language Change." World Englishes 22 (2003): 377--401.
2026 : 01 02 03 04 05 06 07 08 09 10 11 12
2025 : 01 02 03 04 05 06 07 08 09 10 11 12
2024 : 01 02 03 04 05 06 07 08 09 10 11 12
2023 : 01 02 03 04 05 06 07 08 09 10 11 12
2022 : 01 02 03 04 05 06 07 08 09 10 11 12
2021 : 01 02 03 04 05 06 07 08 09 10 11 12
2020 : 01 02 03 04 05 06 07 08 09 10 11 12
2019 : 01 02 03 04 05 06 07 08 09 10 11 12
2018 : 01 02 03 04 05 06 07 08 09 10 11 12
2017 : 01 02 03 04 05 06 07 08 09 10 11 12
2016 : 01 02 03 04 05 06 07 08 09 10 11 12
2015 : 01 02 03 04 05 06 07 08 09 10 11 12
2014 : 01 02 03 04 05 06 07 08 09 10 11 12
2013 : 01 02 03 04 05 06 07 08 09 10 11 12
2012 : 01 02 03 04 05 06 07 08 09 10 11 12
2011 : 01 02 03 04 05 06 07 08 09 10 11 12
2010 : 01 02 03 04 05 06 07 08 09 10 11 12
2009 : 01 02 03 04 05 06 07 08 09 10 11 12
最終更新時間: 2026-01-27 10:29
Powered by WinChalow1.0rc4 based on chalow