hellog〜英語史ブログ / 2020-02-27
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
2020-02-27 Thu
■ #3958. Ritt による中英語開音節長化の公式 [meosl][sound_change][vowel][phonology][phonetics][sonority][neogrammarian][homorganic_lengthening]
昨日の記事「#3957. Ritt による中英語開音節長化の事例と反例」 ([2020-02-26-1]) でみたように,中英語開音節長化 (Middle English Open Syllable Lengthening; meosl) には意外と例外が多い.音環境がほぼ同じに見えても,単語によって問題の母音の長化が起こっていたり起こっていなかったりするのだ.
Ritt (75) は MEOSL について,母音の長化か起こるか否かは,音環境の諸条件を考慮した上での確率の問題ととらえている.そして,次のような公式を与えている (75) .
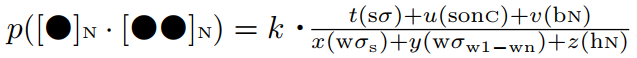
The probability of vowel lenghthening was proportional to
a. the (degree of) stress on it
b. its backness
c. coda sonority
and inversely proportional to
a. its height
b. syllable weight
c. the overall weight of the weak syllables in the foot
In this formula t, u, v, x, y and z are constants. Their values could be provided by the theoretical framework and/or by induction (= trying the formula out on actual data).
これだけでは何を言っているのか分からないだろう.要点を解説すれば以下の通りである.MEOSL が生じる確率は,6つのパラメータの値(および値が未知の定数)の関数として算出される.6つのパラーメタとその効果は以下の通り.
(1) 問題の音節に強勢があれば,その音節の母音の長化が起こりやすい
(2) 問題の母音が後舌母音であれば,長化が起こりやすい
(3) coda (問題の母音に後続する子音)の聞こえ度 (sonority) が高ければ,長化が起こりやすい
(4) 問題の母音の調音点が高いと,長化が起こりにくい
(5) 問題の音節が重いと,長化が起こりにくい
(6) 問題の韻脚中の弱音節が重いと,長化が起こりにくい
算出されるのはあくまで確率であるから,ほぼ同じ音環境にある語であっても,母音の長化が起こるか否かの結果は異なり得るということだ.Ritt のアプローチは,青年文法学派 (neogrammarian) 的な「音韻変化に例外なし」の原則 (Ausnahmslose Lautgesetze) とは一線を画すアプローチである.
なお,この関数は,実は同時期に生じたもう1つの母音長化である同器性長化 (homorganic_lengthening) にもそのまま当てはまることが分かっており,汎用性が高い.同器性長化については明日の記事で.
・ Ritt, Nikolaus. Quantity Adjustment: Vowel Lengthening and Shortening in Early Middle English. Cambridge: CUP, 1994.
2026 : 01 02 03 04 05 06 07 08 09 10 11 12
2025 : 01 02 03 04 05 06 07 08 09 10 11 12
2024 : 01 02 03 04 05 06 07 08 09 10 11 12
2023 : 01 02 03 04 05 06 07 08 09 10 11 12
2022 : 01 02 03 04 05 06 07 08 09 10 11 12
2021 : 01 02 03 04 05 06 07 08 09 10 11 12
2020 : 01 02 03 04 05 06 07 08 09 10 11 12
2019 : 01 02 03 04 05 06 07 08 09 10 11 12
2018 : 01 02 03 04 05 06 07 08 09 10 11 12
2017 : 01 02 03 04 05 06 07 08 09 10 11 12
2016 : 01 02 03 04 05 06 07 08 09 10 11 12
2015 : 01 02 03 04 05 06 07 08 09 10 11 12
2014 : 01 02 03 04 05 06 07 08 09 10 11 12
2013 : 01 02 03 04 05 06 07 08 09 10 11 12
2012 : 01 02 03 04 05 06 07 08 09 10 11 12
2011 : 01 02 03 04 05 06 07 08 09 10 11 12
2010 : 01 02 03 04 05 06 07 08 09 10 11 12
2009 : 01 02 03 04 05 06 07 08 09 10 11 12
最終更新時間: 2026-01-27 10:29
Powered by WinChalow1.0rc4 based on chalow