hellog〜英語史ブログ / 2013-07-07
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
2013-07-07 Sun
■ #1532. 波状理論,語彙拡散,含意尺度 (1) [wave_theory][lexical_diffusion][implicational_scale][dialectology][german][geography][isogloss][consonant][neogrammarian][sgcs][germanic]
「#1506. The Rhenish fan」 ([2013-06-11-1]) の記事で,高地ドイツ語と低地ドイツ語を分ける等語線が,語によって互いに一致しない事実を確認した.この事実を説明するには,青年文法学派 (Neogrammarians) による音韻法則の一律の適用を前提とするのではなく,むしろ波状理論 (wave_theory) を前提として,語ごとに拡大してゆく地理領域が異なるものとみなす必要がある.
いま The Rhenish fan を北から南へと直線上に縦断する一連の異なる方言地域を順に1--7と名付けよう.この方言群を縦軸に取り,その変異を考慮したい子音を含む6語 (ich, machen, dorf, das, apfel, pfund) を横軸に取る.すると,Second Germanic Consonant Shift ([2010-06-06-1]) の効果について,以下のような階段状の分布を得ることができる(Romain, p. 138 の "Isoglosses between Low and High German consonant shift: /p t k/ → /(p)f s x/" より).
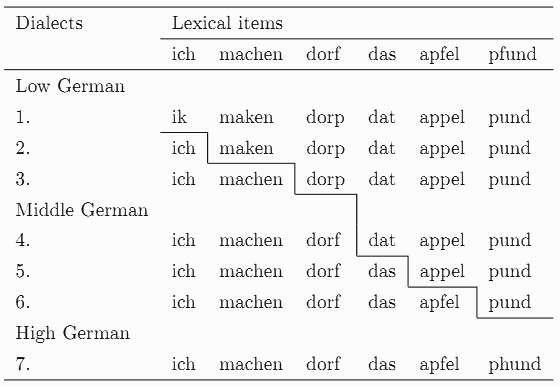
方言1では SGCS の効果はゼロだが,方言2では ich に関してのみ効果が現われている.方言3では machen に効果が及び,方言4では dorf にも及ぶ.順に続いてゆき,最後の方言7にいたって,6語すべてが子音変化を経たことになる.1--7が地理的に直線上に連続する方言であることを思い出せば,この表は,言語変化が波状に拡大してゆく様子,すなわち波状理論を表わすものであることは明らかだろう.
さて,次に1--7を直線上に隣接する方言を表わすものではなく,ある1地点における時系列を表わすものとして解釈しよう.その地点において,時点1においては SGCS の効果はいまだ現われていないが,時点2においては ich に関して効果が現われている.時点3,時点4において machen, dorf がそれぞれ変化を経て,順次,時点7の pfund まで続き,その時点にいたってようやくすべての語において SGCS が完了する.この解釈をとれば,上の表は,時間とともに SGCS が語彙を縫うようにして進行する語彙拡散 (lexical diffusion) を表わすものであることは明らかだろう.
縦軸の1--7というラベルは,地理的に直線上に並ぶ方言を示すものととらえることもできれば,時間を示すものととらえることもできる.前者は波状理論を,後者は語彙拡散を表わし,言語変化論における両理論の関係がよく理解されるのではないか.
さらに,この表は言語変化に伴う含意尺度 (implicational scale) を示唆している点でも有意義である.6語のうちある語が SGCS をすでに経ているとわかっているのであれば,その方言あるいはその時点において,その語より左側にあるすべての語も SGCS を経ているはずである.このことは右側の語は左側の語を含意すると表現できる.言語変化の順序という通時的な次元と,どの語が SGCS の効果を示すかが予測可能であるという共時的な次元とが,みごとに融和している.
音韻変化と implicational scale については,「#841. yod-dropping」 ([2011-08-16-1]) も参照.
・ Romain, Suzanne. Language in Society: An Introduction to Sociolinguistics. 2nd ed. Oxford: OUP, 2000.
2026 : 01 02 03 04 05 06 07 08 09 10 11 12
2025 : 01 02 03 04 05 06 07 08 09 10 11 12
2024 : 01 02 03 04 05 06 07 08 09 10 11 12
2023 : 01 02 03 04 05 06 07 08 09 10 11 12
2022 : 01 02 03 04 05 06 07 08 09 10 11 12
2021 : 01 02 03 04 05 06 07 08 09 10 11 12
2020 : 01 02 03 04 05 06 07 08 09 10 11 12
2019 : 01 02 03 04 05 06 07 08 09 10 11 12
2018 : 01 02 03 04 05 06 07 08 09 10 11 12
2017 : 01 02 03 04 05 06 07 08 09 10 11 12
2016 : 01 02 03 04 05 06 07 08 09 10 11 12
2015 : 01 02 03 04 05 06 07 08 09 10 11 12
2014 : 01 02 03 04 05 06 07 08 09 10 11 12
2013 : 01 02 03 04 05 06 07 08 09 10 11 12
2012 : 01 02 03 04 05 06 07 08 09 10 11 12
2011 : 01 02 03 04 05 06 07 08 09 10 11 12
2010 : 01 02 03 04 05 06 07 08 09 10 11 12
2009 : 01 02 03 04 05 06 07 08 09 10 11 12
最終更新時間: 2026-01-27 10:29
Powered by WinChalow1.0rc4 based on chalow