hellog〜英語史ブログ / 2013-07-08
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
2013-07-08 Mon
■ #1533. 波状理論,語彙拡散,含意尺度 (2) [wave_theory][neogrammarian][lexical_diffusion][implicational_scale][phonetics][ot]
昨日の記事[2013-07-07-1]に引き続き,言語変化にまつわる3つの概念の関係について.昨日は,Second Germanic Consonant Shift ([2010-06-06-1]) がいかに地理的に波状に拡大し,どのような順序で語彙を縫って進行したかという話題を取り上げた.今日は,英語の諸変種にみられる -t/-d deletion という現象に注目する.
-t/-d deletion とは,missed, grabbed, mist, hand などの語末の歯閉鎖音が消失する音韻過程である.非標準的で略式の発話ではよくみられる現象だが,その生起頻度は形態音韻環境によって異なると考えられている.関与的な形態音韻環境とは,問題の語が (1) mist のように1形態素 (monomorphemic) からなるか miss-ed のように2形態素 (bimorphemic) からなるか,(2) 後続する音が子音か (ex. missed train) 母音か (ex. missed Alice) の2点である.(1) 1形態素 > 2形態素, (2) 子音後続 > 母音後続という関係が成り立ち,1形態素で子音後続の -t/-d が最も消失しやすく,2形態素で母音後続の -t/-d が最も消失しにくいということが予想される.この予想を mist と missed に関して表の形に整理すると,以下のようになる(Romain, p. 142 の "Temporal development of varieties for the rule of -t/-d deletion" より).
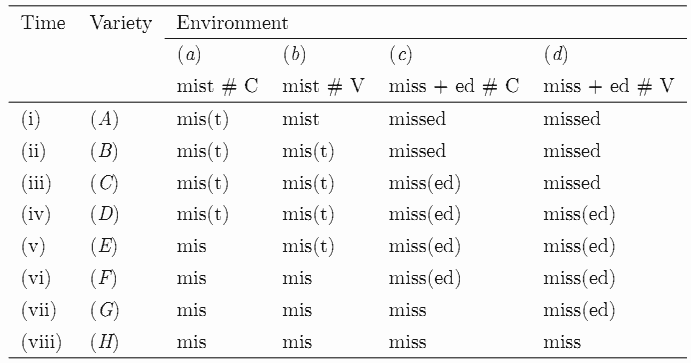
これは,昨日の SGCS の効き具合を示す表と類似している.ここでは,変種(方言),時点,形態音韻環境に応じて,-t deletion の効き具合が階段状の分布をなしている.隣接変種への拡がりとみれば波状理論を表わすものとして,時系列でみれば語彙拡散を表わすものとして,通時的な順序の共時的な現われとみれば含意尺度を表わすものとして,この表を解釈することができる.
2種類の形態音韻環境については,-t/-d deletion の効き具合に関する制約 (constraint) ととらえることもできる.(1) は有意味な接尾辞形態素 -ed は消失しにくいという制約,(2) は煩瑣な子音連続を構成しない -t/-d は消失しにくいという制約として再解釈できる.この観点からすると,2つの制約の効き具合の優先順位によって,異なった -t/-d deletion の分布表が描かれることになるだろう.ここにおいて,波状理論,語彙拡散,含意尺度といった概念と,Optimality Theory (最適性理論)との接点も見えてくるのではないか.
・ Romain, Suzanne. Language in Society: An Introduction to Sociolinguistics. 2nd ed. Oxford: OUP, 2000.
2026 : 01 02 03 04 05 06 07 08 09 10 11 12
2025 : 01 02 03 04 05 06 07 08 09 10 11 12
2024 : 01 02 03 04 05 06 07 08 09 10 11 12
2023 : 01 02 03 04 05 06 07 08 09 10 11 12
2022 : 01 02 03 04 05 06 07 08 09 10 11 12
2021 : 01 02 03 04 05 06 07 08 09 10 11 12
2020 : 01 02 03 04 05 06 07 08 09 10 11 12
2019 : 01 02 03 04 05 06 07 08 09 10 11 12
2018 : 01 02 03 04 05 06 07 08 09 10 11 12
2017 : 01 02 03 04 05 06 07 08 09 10 11 12
2016 : 01 02 03 04 05 06 07 08 09 10 11 12
2015 : 01 02 03 04 05 06 07 08 09 10 11 12
2014 : 01 02 03 04 05 06 07 08 09 10 11 12
2013 : 01 02 03 04 05 06 07 08 09 10 11 12
2012 : 01 02 03 04 05 06 07 08 09 10 11 12
2011 : 01 02 03 04 05 06 07 08 09 10 11 12
2010 : 01 02 03 04 05 06 07 08 09 10 11 12
2009 : 01 02 03 04 05 06 07 08 09 10 11 12
最終更新時間: 2026-01-19 11:07
Powered by WinChalow1.0rc4 based on chalow