hellog〜英語史ブログ / 2011-06-25
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
2011-06-25 Sat
■ #789. Chaucer の trochaic substitution [chaucer][meter]
中英語の韻文形式の典型といえば,13世紀後半に始まる The Poema Morale や The Owl and the Nightingale などの iambic tetrameter や,Chaucer に代表される iambic pentameter が挙げられる.この形式は弱強格 ( iamb ) の強勢交替を特徴とするが,あまりに規則正しい弱強格の繰り返しは単調さを招くために,時にこの規則が破られ強弱格 ( trochee ) の現われることがある.これは trochaic substitution と呼ばれ,中英語詩では珍しくない.
例えば,次の Chaucer の詩行 (GP 105) では,第1詩脚で trochaic substitution が生じている.
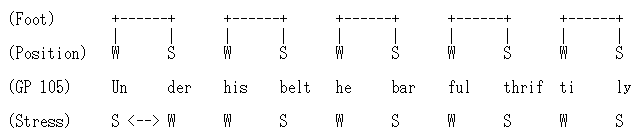
trochaic substitution により「強弱弱」という3拍子が生じることになるが,この3拍子自体は口語英語では普通のことだったし,Ormulum などの早い段階での中英語詩にも確認される.また,イタリア語詩など大陸の詩では2拍子と3拍子の繰り返しの形式が見られ,中英語の3拍子が突飛な形式なわけではない.
詩行のどの位置(詩脚)で substitution が生じやすいかを調査した研究がある.以下は,Li (1995) の数値に基づいて Minkova (191) が提示している,Chaucer の韻文コーパス全体における substitution の比率である.
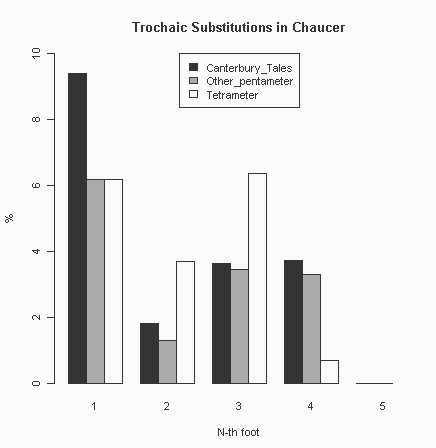
一般に詩行は頭部で自由度が高く,尾部で自由度が低い.尾部で融通が利かないのは,脚韻位置であり,脚韻を担う音節は必ず強勢を伴わなければならないという制約があるためである.一方で,頭部は気楽に始められるために,融通が利きやすい.CT でとりわけ substitution 比率が高いのは,同作品における会話体の豊富さを示しているように思われる
Minkova (191) より,各詩脚からの substitution の例を挙げよう.
- Redy to wenden on my pilgrimage (GP 21)
- Of his offryng and eek of his substaunce. (GP 489)
- Ful semely after hir mete she raughte. (GP 136)
- The smylere with the knyf under the cloke (KnT 1999)
・ Minkova, Donka. "The Forms of Verse" A Companion to Medieval English Literature and Culture: c.1350--c.1500. Ed. Peter Brown. Malden, MA: Blackwell, 2007. Malden, MA: Wiley-Blackwell, 2009. 176--95.
・ Li, Xingzhong. "Chaucer's Metres." Diss. U of Missouri, Columbia. 1995.
2026 : 01 02 03 04 05 06 07 08 09 10 11 12
2025 : 01 02 03 04 05 06 07 08 09 10 11 12
2024 : 01 02 03 04 05 06 07 08 09 10 11 12
2023 : 01 02 03 04 05 06 07 08 09 10 11 12
2022 : 01 02 03 04 05 06 07 08 09 10 11 12
2021 : 01 02 03 04 05 06 07 08 09 10 11 12
2020 : 01 02 03 04 05 06 07 08 09 10 11 12
2019 : 01 02 03 04 05 06 07 08 09 10 11 12
2018 : 01 02 03 04 05 06 07 08 09 10 11 12
2017 : 01 02 03 04 05 06 07 08 09 10 11 12
2016 : 01 02 03 04 05 06 07 08 09 10 11 12
2015 : 01 02 03 04 05 06 07 08 09 10 11 12
2014 : 01 02 03 04 05 06 07 08 09 10 11 12
2013 : 01 02 03 04 05 06 07 08 09 10 11 12
2012 : 01 02 03 04 05 06 07 08 09 10 11 12
2011 : 01 02 03 04 05 06 07 08 09 10 11 12
2010 : 01 02 03 04 05 06 07 08 09 10 11 12
2009 : 01 02 03 04 05 06 07 08 09 10 11 12
最終更新時間: 2026-01-27 10:29
Powered by WinChalow1.0rc4 based on chalow