hellog〜英語史ブログ / 2012-02-04
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
2012-02-04 Sat
■ #1013. アングロサクソン人はどこからブリテン島へ渡ったか [geography][toponymy][onomastics][map][patronymy][anglo-saxon]
固有名詞学 (onomastics) のなかでも地名学 (toponymy) は,言語学と歴史学が濃密に接する分野である.[2011-07-24-1]の記事「#818. イングランドに残る古ノルド語地名」でみたように,地名の構成と分布は,民族の歴史的な行動をありありと示してくれることがある.昨日の記事「#1012. 古代における英語からフランス語への影響」 ([2012-02-03-1]) で参照した Martinet の論文は,フランス北部に残る英語式に構成された地名の分布から,標題の疑問に迫る論考である.
英語式の地名の典型の1つに,単音節+ -ing + -ham/-ton」という形態がある (ex. Buckingham, Nottingham, Birmingham; Padington, Islington, Arlington) .-ing は英語の典型的な父称 (patronym) 接辞であり,-ham は home に,-ton は town に対応する.おもしろいことに,フランスにも,フランス語化されている部分はあるが,Tardinghen, Bouquinghen, Tatinghem, Conincthun, Verlingcthun, Audincthun など,明らかに英語地名のモデルに基づいた地名がある.それも,フランス北部の Artois (現在の Pas-de-Calais 県の一部にあたる地方),特に Boulogne から Saint Omer にかけての地域に集中している.Martinet (6--7) の地図によれば,この種の英語地名が77個も確認される.
この英語地名の分布が示唆するのは,かつてこの地方に,後の英語話者と密接に結びつけられる Anglo-Frisian 系の西ゲルマン民族が定住していたということである.彼らはブリテン島に渡る際の中継点としてこの地を通り過ぎただけではなく,この地に住み着いて,南に接する Gallo-Roman (後にフランス語へ発達する言語)に言語的な影響を与え得るほどに存在感を示していた可能性が高い.
Martinet は,以上の証拠と,イギリス海峡の両側に位置する主要な地点間の距離を考慮して,次のような仮説を提案している.
On est tenté de poser Boulogne, au nom celtique, comme le passage normal des deux vagues d'envahisseurs celtes qui ont passé la Manche avant notre ère. La distance de Boulogne au cap Dungeness est indiquée en pensant aux Saxons qui ont peuple le Wessex. / Notre hypothèse n'exclut pas un passage plus direct par la mer du Nord, mais le Jutland est à plus de 500 km des côtes anglaises. (10)
紀元前に2波にわたってイギリス海峡を横断したケルト人の侵略者たちの通常の経路としては,ケルト語の地名を帯びたブローニュを想定したいところだ.サクソン人がウェセックスに植民したことを考えれば,ブローニュからダンジネス岬の距離は適切だろう.この仮説は,北海を越えるより直接の経路を排除するわけではないが,ユットランドはイギリスの海岸から500キロ以上も離れているのだ.
サクソン人が,かつてケルト人の開拓したブローニュから海に出るというルートを利用し,イギリス側ではウェセックス植民に都合のよい,かつ航海距離の短いダンジネス岬に着岸した,というわけだ.従来より,アングロサクソン人は航海に長けていたはずだとの前提から,[2010-05-21-1]の記事「#389. Angles, Saxons, and Jutes の故地と移住先」の地図で概略的に示したように,北海をはるばる越えてのルートが想定されてきたが,地名分布に支えられた Martinet の仮説も魅力的だ.
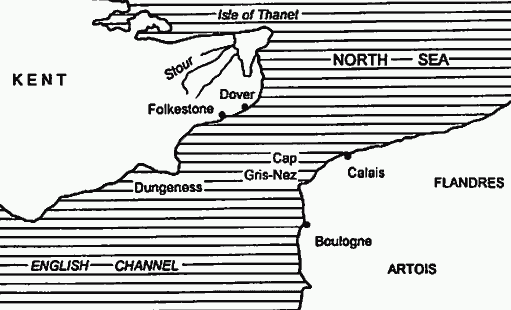
(Martinet, p. 9 の地図を掲載)
・ Martinet, André. "Comment les Anglo-Saxons ont-ils accédé à la Grande-Bretagne?" La Linguistique 32.2 (1996): 3--10.
2026 : 01 02 03 04 05 06 07 08 09 10 11 12
2025 : 01 02 03 04 05 06 07 08 09 10 11 12
2024 : 01 02 03 04 05 06 07 08 09 10 11 12
2023 : 01 02 03 04 05 06 07 08 09 10 11 12
2022 : 01 02 03 04 05 06 07 08 09 10 11 12
2021 : 01 02 03 04 05 06 07 08 09 10 11 12
2020 : 01 02 03 04 05 06 07 08 09 10 11 12
2019 : 01 02 03 04 05 06 07 08 09 10 11 12
2018 : 01 02 03 04 05 06 07 08 09 10 11 12
2017 : 01 02 03 04 05 06 07 08 09 10 11 12
2016 : 01 02 03 04 05 06 07 08 09 10 11 12
2015 : 01 02 03 04 05 06 07 08 09 10 11 12
2014 : 01 02 03 04 05 06 07 08 09 10 11 12
2013 : 01 02 03 04 05 06 07 08 09 10 11 12
2012 : 01 02 03 04 05 06 07 08 09 10 11 12
2011 : 01 02 03 04 05 06 07 08 09 10 11 12
2010 : 01 02 03 04 05 06 07 08 09 10 11 12
2009 : 01 02 03 04 05 06 07 08 09 10 11 12
最終更新時間: 2026-01-27 10:29
Powered by WinChalow1.0rc4 based on chalow