hellog〜英語史ブログ / 2010-08-20

■ #480. father とヴェルネルの法則 [grimms_law][verners_law]

　ヴェルネルの法則 ( Verner's Law ) については，[2009-08-09-1]の記事で hundred という語を用いて説明した．多くの参考書では Verner's Law の説明に father が用いられているので，今日は father を用いた教科書的な記述を試みる．
　Verner's Law は，語によってグリムの法則 ( Grimm's Law ; see [2009-08-08-1], [2009-08-07-1]) の予想に反する形態が出力されてしまう問題に対して，印欧祖語の段階でのアクセントの位置を考慮することで解決を図ろうとして見つけだされた法則である．「父」を表わす印欧祖語の再建形は である．語頭の *p は Grimm's Law に従ってゲルマン諸語へは f として伝わった．古英語の形態は fæder であるから，これについては法則通りである．だが，第2子音を考えると具合が悪い．印欧祖語の *t は Grimm's Law に従えばゲルマン諸語では th に対応するはずだが，実際には古英語の場合の fæder にあるように d に対応している．（ここで現代英語の形態 father を思い浮かべてはいけない．現代の英語の形態に見られる th は後述するように中英語後期からの発達で，Grimm's Law の出力と直接に関連づけるのはアナクロである．）
　一見すると Grimm's Law はここで破綻するが，1875年に Karl Verner (1846--96) がこの例外を説明する別の法則を発見した．「アクセントが先行しない，有声音にはさまれた環境における *t は，グリムの法則の予想する *θ にはならず，それが有声化した音である ð になる」というものである．印欧祖語の再建形によればアクセントは第2音節にあり，*t にとってはアクセントが先行しないことになる．さらに有声母音にはさまれているので，上記の環境に合致する．したがって，予想される *θ にはならずに，代わりに *ð へ変化したとして説明される．だが，ここではまだ古英語の fæder にたどり着かない．Verner's Law を経た後に，この語のアクセントが第1音節に移動し（＝ゲルマン語派の特徴の1つ），さらに古英語を含む西ゲルマン語群では当該子音 *ð が脱摩擦音化して d となった．こうしてようやく（母音は別として）めでたく古英語の fæder が出力されることになる．
　だが，話しはまだ終わらない．古英語で d となった第2子音は，後期中英語期の1400年以降に再び摩擦音化し，ð へと回帰してゆく．入力の印欧祖語形と出力の現代英語形を並べてみると，Grimm's Law と Verner's Law の適用のみを考えればよいように思われるが，実際には Verner's Law の後にアクセント移動，脱摩擦音化，摩擦音化という各種の音声変化を経て結果的に回帰したにすぎない．こうして，ようやく現代英語の father にたどり着くのである．
　このように見てきて分かるように，father は (1) 古英語以降にも数々の音声変化を経ているために印欧祖語形から現代英語形に至るまでの道のりが非常に遠く，(2) 現代の綴りに <th> があることから Grimm's Law で予想される出力の *θ や Verner's Law で予想される出力の *ð と現代英語形がアナクロに結びつけられやすい，という事情があり，Verner's Law を解説する例としては father はあまり適切ではない．この語の音声変化は相当に複雑なのである．それで[2009-08-09-1]の記事ではワンステップだけ行程の少ない hundred の例を持ち出したのだが，英語の音声変化が Grimm's Law や Verner's Law のような著名なものばかりではなく，細かいところでいろいろと起こっているのだということを思い出させるには father もよい例かもしれない．まとめとして以下の図を参照．



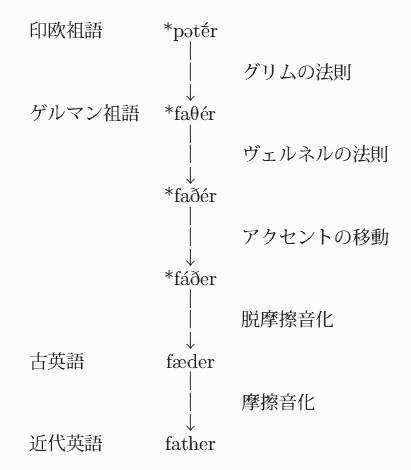
　・寺澤 盾　『英語の歴史』　中央公論新社〈中公新書〉，2008年. 31--33頁．

[ 固定リンク | 印刷用ページ ]