hellog〜英語史ブログ / 2017-11-02
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
2017-11-02 Thu
■ #3111. カオス理論と言語変化 (1) [chaos_theory][language_change][complex_system]
1960年代より,カオス理論 (chaos_theory) は「時計じかけの宇宙」観に代わる自然科学のパラダイムとして受け入れられてきたのみならず,社会科学その他の領域へも応用されてきた.それは,気象学,物理学,天文学,数学に始まり,生物学,経済学,社会学にまで裾野を広げている.例えば,気象現象,流体力学,幾何学,生物の個体数の増加速度,立ち上る煙の振る舞い,綿花の価格などがカオス理論で説明されるといわれ,ほかには実用的なところでCGの描画にも活用されている.
カオス理論は,その名前とは裏腹に,実は秩序に関する理論である.一見ランダムで予測できない現象にも,ある種の傾向が見られると主張する.また,カオス理論は,初期条件が僅かに異なるだけでも,その後の振る舞いに甚大な影響が及ぼされる点を指摘する.その最も有名な例がバタフライ効果 (butterfly effect) だろう.『サイエンス大図鑑 コンパクト版』 (351) によれば,バタフライ効果とは,
カオス系の主な特徴である「初期条件に大きく左右される性質」を表現するために,エドワード・ローレンツが考案した用語.初期条件の変更がたとえわずかであっても,現象が何度も繰り返されるうちに,大きな差が生じてしまうことを示す.ローレンツは「蝶(バタフライ)がブラジルで羽ばたくと,テキサスで竜巻が起こる」と表現した.彼のデータから描かれたモデル“ローレンツ・アトラクタ”は,偶然にも蝶の形をしている.カオス的な現象の進行を示すこのモデルでは,突然,進行方向が逆転し,同じ軌跡は2度と通らない.
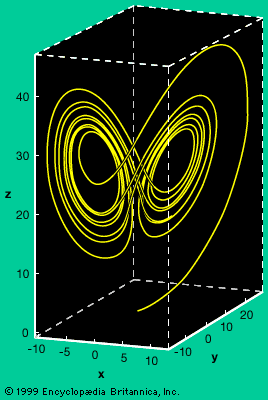
"Lorenz' attractor" と呼ばれる蝶を彷彿とさせるこの3次元のグラフは,天候の軌跡を表現している.開始点の座標がたとえ僅かでも異なると,軌道が大きく逸脱し,異なる羽形の領域(各々穏やかな天候と荒れた天候を表わす)へ帰着するという.
初期条件の僅かな異なりが後に甚大な差異をもたらす現象を,数学の簡単な例で確かめることができる.A を定数(ここでは A = 2 とおく)とし,x0 を0から1の間をとるものとする(ここでは x0 = 0.9 とおく).このとき,x1 を Ax0(1 - x0) と定義すれば,x1 = 2 * 0.9 * (1 - 0.9) = 0.18 となる.同様に,x2 = Ax1(1 - x1) = 2 * 0.18 * (1 - 0.18) = 0.2952 とし,このサイクルを繰り返して,x0 から xn までの数列を得る.結果は,0.09, 0.18, 0.2952, 0.4161, 0.4859, 0.4996, 0.5000, 0.5000, ... となり,0.5000で安定する.A の値を2から3まで大きくしても,安定期に入るまでのサイクル数は増えるものの,最終的には安定する.これは,振り子が多少乱されても,最終的には揺れが安定してくることになぞらえられる.
ところが,A が3を超えると,2つの数を行き来する関係に至るなど予期できない振る舞いを示すようになる.そして,A が3.57程度になると,いつまでたっても定期性を示さない状態,すなわちカオスの状態に帰結する.例えば,A を3.7とおき,初期値の x0 を 0.9 と置いた場合と,僅かに異なる 0.9000009 と置いた場合の数列を得てグラフをプロットすると,以下のように興味深い結果が得られる.
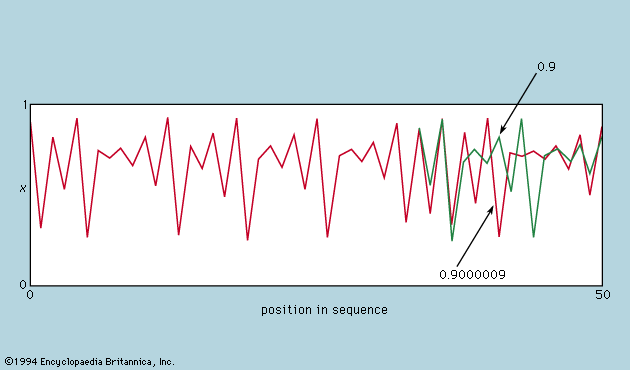
35サイクルまでは2つのグラフは事実上重なっているが,以降40サイクルくらいまでにある種の安定的な分岐を示すようになり,その後は互いに無関係のカオス的な様相を呈する.すべては,初期値の僅かな差に由来するのだ.見方を変えれば,種々の初期条件がほぼ一致していたとしても,ある1つの条件において0.000009ほどの差があれば,後にたどる運命を天と地ほどまで違えるのに十分であるということになる.
カオス理論は,「環境」が関与するありとあらゆる分野に適用されることが明らかになってきている.言語とその変化も「環境」のなかで作用しているものであるから,当然,カオス理論と無縁ではない.例えば,拙著『英語の「なぜ?」に答える はじめての英語史』の「3.5.2 -e の衰退の一波万波」で示したとおり,英語史における屈折語尾の弱化という調音の僅かな変化が引き金となって,英語の統語論ががらんと組み替えられた事例が,カオス理論のバタフライ効果に対応するだろうか.言語も,「一波動けば万波生ず」なのである.
明日の記事でも,引き続きカオス理論の話題を扱う.
・ デイヴィス,アダム・ハート(総監修),日暮 雅通(監訳) 『サイエンス大図鑑 コンパクト版』 河出書房新社,2014年.
・ 堀田 隆一 『英語の「なぜ?」に答えるはじめての英語史』 研究社,2016年.
2026 : 01 02 03 04 05 06 07 08 09 10 11 12
2025 : 01 02 03 04 05 06 07 08 09 10 11 12
2024 : 01 02 03 04 05 06 07 08 09 10 11 12
2023 : 01 02 03 04 05 06 07 08 09 10 11 12
2022 : 01 02 03 04 05 06 07 08 09 10 11 12
2021 : 01 02 03 04 05 06 07 08 09 10 11 12
2020 : 01 02 03 04 05 06 07 08 09 10 11 12
2019 : 01 02 03 04 05 06 07 08 09 10 11 12
2018 : 01 02 03 04 05 06 07 08 09 10 11 12
2017 : 01 02 03 04 05 06 07 08 09 10 11 12
2016 : 01 02 03 04 05 06 07 08 09 10 11 12
2015 : 01 02 03 04 05 06 07 08 09 10 11 12
2014 : 01 02 03 04 05 06 07 08 09 10 11 12
2013 : 01 02 03 04 05 06 07 08 09 10 11 12
2012 : 01 02 03 04 05 06 07 08 09 10 11 12
2011 : 01 02 03 04 05 06 07 08 09 10 11 12
2010 : 01 02 03 04 05 06 07 08 09 10 11 12
2009 : 01 02 03 04 05 06 07 08 09 10 11 12
最終更新時間: 2026-02-21 08:56
Powered by WinChalow1.0rc4 based on chalow