complex_system - hellog〜英語史ブログ

■ #5072. 機械も人間も無限に増えていく語彙を学習し続けている [social_media][vocabulary][nlp][complex_system][dynamic_equilibrium]

　この2日間の記事「#5070. ソーシャルメディアと中英語の綴字のヴァリエーションは酷似している」 ([2023-03-15-1]) と「#5071. ソーシャルメディアは自然言語データの最大の発生源である」 ([2023-03-16-1]) に引き続き，ソーシャルメディアの言語について．今回は同メディアにおける語彙の増加率が著しい件を取り上げる．
　Vajjala 他 (296) に「増え続ける語彙」という1節がある（引用中の図の再掲は省略する）．

ほとんどの言語では，毎年新しい単語が増えることはほとんどありません．しかし，「ソーシャルの言語」では，非常に早いスピードで語彙が増えています．毎日のように新しい単語が現れるのです．つまり，ソーシャルメディアのテキストを処理する NLP システムは，学習データの語彙に含まれていない大量の新語を扱うことになります．
この問題の深刻さを知るために，図8-5を見てみましょう．これは数年前に行った実験で，大規模なツイートのコーパスを集め，月ごとに新語の数を可視化したものです．この図は，1か月間に見られた新語の割合を前月のデータと比較しています．画像からもわかるように，前月の数字と比較すると，毎月10～15%の新しい単語が増えています．

　冒頭の「ほとんどの言語では，毎年新しい単語が増えることはほとんどありません」は正確ではないが，ソーシャルメディアでの語彙増加率として提示されている「10～15%」を信じるならば，それと比較して微々たるものだという主張としては受け入れられそうだ．
　自然言語処理のシステムは，このような日々の語彙爆発に対応するために，新単語をひたすら学習し，語彙体系を最新状態に保たなければならない．疲れ知らずの機械とはいえ，処理効率を維持するにあたり，大きな負荷になっているという．自然言語処理のシステムは，そもそも動的に更新されなければならない宿命なのである．
　システムの動的性格について，Vajjala 他は別の箇所で次のようにも述べている (398) ．

NLP のモデルは，静的なものではありません．本番環境でも頻繁にモデルの更新を求められます．これについてはいくつかの理由があります．本番環境では，以前の学習データとは異なる，より多くの（そしてより新しい）データを得られます．この変化に合わせてモデルを更新しなければ，モデルはすぐに陳腐化してしまい，予測性能は低下するでしょう．また，モデルの予測が間違っている場合について，ユーザーからフィードバックを得られることがあります．その際には，モデルとその特徴を反映し，適宜修正を加える必要があります．いずれの場合も，現行モデルを定期的に再学習して更新し，新しいモデルを本番にデプロイするプロセスを構築する必要があります．

　ここまで考察して，これは機械による自然言語処理のシステムに限った話しではなく，まさに人間の言語処理にもそのまま当てはまることだと気づいた．人間も，周囲で生じている言語環境の変化に合わせて常に言語体系を最新状態に更新しているのであり，その点では特に機械と異なるところはない．言語は複雑系 (complex_system) の動的システムであり，動的平衡 (dynamic_equilibrium) を保ちながら機能し続けているのである．
　人間の言語知識を再現しようとしている自然言語処理の分野の知見が，むしろ人間の言語知識とは何かという問いに示唆を与えてくれる1例ではないか．

　・ Vajjala, Sowmya, Bodhisattwa Majumder, Anuj Gupta, Harshit Surana （著），中山 光樹（訳）　『実践　自然言語処理 --- 実世界 NLP アプリケーション開発のベストプラクティス』　オライリー・ジャパン，2022年．

[ 固定リンク | 印刷用ページ ]

■ #5015. 会話の成り立ちとカオス [chaos_theory][complex_system]

　言語とカオス理論 (chaos_theory) や複雑系 (complex_system) の関わりについては，これまでの記事でも触れることがあった．過去の記事では，主に言語体系の安定性や言語の統計的振る舞いを念頭に，カオスとの関わりに注目してきた．
　たまたま『新編　認知言語学キーワード事典』 (p. 34) を開いていて「カオス (chaos)」の項を発見した．そこではカオス理論の基本が解説された後に，会話の成り立ちとカオスの関係について紹介されている．私にとって斬新な視点だった．以下に引用する．

カオス現象は，例えば，木の葉の落下軌道，昆虫の大量発生，煙草の煙やパチンコの玉の動き，伝染病の流行，株式市況，波の砕け方，雲の動きなど，自然界ではごく普通に見られるが，注目すべきは，カオスという不規則で予測不可能な現象が，比較的単純な決定論的 (deterministic) な規則に従う中で生じるということである．決定論とは，最初の状態が決まれば任意の時点での状態が一義的に決まるというものを言う．ニュートン流の古典物理学では，単純な現象は単純な原因で生じ複雑な減収は複雑な原因で生じるものとされていたが，カオス研究は，決定論的規則に従っている場合には，複雑で予測不可能な現象が生じることを示すもので，古典物理学の常識を覆すとともに，ランダムにしか見えない複雑な現象でも単純な規則性を持つ可能性があり，その過程を明らかにする必要性をわれわれに訴えている．
　言語との関連で言うと，カオス的な現象は，会話の成り立ちにおいて端的に現れる．実際，会話に際して一定のルールを定め，そのルールを完全に守って自由会話を始めたとしても，時間の進行とともに，会話の展開や内容は予想できないものになる．また，同じルールでも初期条件を少し変えるだけで，その後に展開される会話の内容が大きく変わるという点でも，カオス的な振る舞いを見せる．また，関連語として，秩序（予測可能な構造）から無秩序（カオス）へ転換するところを「カオスの縁」 (edge of chaos) と言い，カオスの縁は有機的な領域で，情報発生能力が高いところである．

　一定のルールを守るとしても，フリートークの場合，会話の成り立ちや進み方は確かに先が読めないことも多い．言語体系とは別軸で，言葉に関わるカオス的な現象は，思いのほかいろいろなところに観察されるのかもしれない．

　・ 辻 幸夫（編）　『新編　認知言語学キーワード事典』　研究社．2013年．

[ 固定リンク | 印刷用ページ ]

■ #4679. 言語における塊現象とゆらぎ [complex_system][computational_linguistics][statistics][frequency][1/f][terminology][keyword]

　昨日の記事「#4678. 言語における塊現象と長相関」 ([2022-02-16-1]) で，言語における塊現象を「長相関」の観点からみたが，今回はもう1つの観点である「ゆらぎ」に注目しよう．ゆらぎ解析について，田中 (112) は次のように説明している．

このような塊現象を捉える自然な方法の一つとして，ある一定の範囲内に出現する単語の頻度の分散を調べることが挙げられる．ある単語の出現にゆらぎがあるのであれば，ある一定の範囲内にその単語が出現しない場合があり，また一方でその単語が数多く出現する場合もあり，その頻度の分散は大きくなるはずである．

　解析原理としては分かりやすい．ある文章中に表われる語彙を念頭におく場合，ゆらぎ方は語によって異なるが，おもしろいことに，いわゆるキーワードはしばしばゆらぎが大きいという（田中，p. 118）．これは，機械的なキーワードの同定などに貢献しそうな興味深い傾向である．
　また，人間言語による文章とランダム文字列の文章とでゆらぎを比べると，明らかに前者の方がゆらぎが大きく，このことは人間言語の特徴の一端を示唆する．さらに，文章のジャンルによってもゆらぎは異なるために（田中，p. 120），ゆらぎの度合いは文体論的な指標ともなり得る．
　様々な可能性を秘めた言語における「ゆらぎ」にアンテナを張っておきたい．関連して「1/f ゆらぎ」 (1/f) も要注目．

　・ 田中 久美子　『言語とフラクタル --- 使用の集積の中にある偶然と必然』　東京大学出版会，2021年．

[ 固定リンク | 印刷用ページ ]

■ #4678. 言語における塊現象と長相関 [complex_system][computational_linguistics][statistics][frequency][information_structure][article][terminology]

　言語には，他の多くの自然・社会現象にもみられる「塊現象」というものが観察される．田中 (98) の説明を引用する．

その傾向は一言で言えば「塊現象」，つまり単語が固まって現れること，ある単語が一旦現れるとしばらくの間は頻繁に出現する一方で，それを過ぎるとほとんど出現しなくなる傾向があることとして直感的に捉えることができる．塊現象が見られる系列では，短い間隔が続いた後には短い間隔が現れ，また逆に長い間隔が続いた後には長い間隔が現れる可能性が高い．このような言語の塊現象の要因の一つは，当然のことながら文脈の変化にある．
　塊現象は，自然，金融など，さまざまな複雑系においてはよく知られる〔中略〕．たとえば，大雨や地震が固まって現れることは経験を通して誰しも知っているだろう．社会的な対象においても，たとえば，株取引には，ある取引が引き金となって，関連する取引が行われるため，やはり塊現象が生じることが知られる．同様に，単語もある単語が引き金となり，その単語ならびに関連する単語の塊が出現する．

　説明されてみれば，もっともという現象ではある．この塊現象の一般的な研究には歴史があるが，言語に応用した研究は少ないようだ．解析法としては，大きく分けて「長相関」と「ゆらぎ」に着目する2種類があるという．ここでは前者を見ていこう．
　「長相関」による解析は，「ある系列中の，二つの部分列の相関が，その部分列の距離 s に依存してどのように変化するかを調べる解析」である（田中，p. 99）．互いに離れた2つの部分列の内部構造が類似していれば長相関があるということになる（cf. 「#4675. 言語と複雑系」 ([2022-02-13-1]) で言及した「長期記憶」）．
　英語における最頻語である定冠詞 the について，長い文章で長相関解析を試みると，どうやら弱い長相関があるようだ（田中，p. 105）．しかし，あくまで弱い長相関があるにとどまり，細かくみれば the にすらある程度の塊現象がみられることが判明する．驚くことに，the も現われるときは固まって現われ，現われないときにはしばらく現われない，ということがある程度観察されるのである．田中 (109）は，先行研究に従い，この事実を次のように解釈している．

k 個の短い間隔があると，続く k + 1番目の間隔も短く，k 個の長い間隔があると，それに続く k + 1番目の間隔も長い傾向にある．短い間隔が続くことは，対象となる単語が固まって現れることを示している．〔中略〕このような塊現象の背景には文脈の変化がある．the については，まず不定冠詞を中心として一般的な概念を導入し，その後，導入された概念について議論が行われ，その際は the が多用される．

　これは，談話における情報構造 (information_structure) に着目した，the についての塊現象の読み解きといってよいだろう．

　・ 田中 久美子　『言語とフラクタル --- 使用の集積の中にある偶然と必然』　東京大学出版会，2021年．

[ 固定リンク | 印刷用ページ ]

■ #4675. 言語と複雑系 [complex_system][chaos_theory][1/f][terminology]

　標題については「#3130. 複雑系言語学」 ([2017-11-21-1]) をはじめとして complex_system の記事で垣間見てきた．一昨日の記事「#4673. 言語の統計的必然性と偶然性」 ([2022-02-11-1]) で参照した田中が，『言語とフラクタル』の導入部で「複雑系」と題する1節を書いている．p. 34--35 より要点を引用したい．

本書における複雑系は，以下の二つの大域的な性質が満たされるものとして定義される．

　・ 要素の分布にスケールフリー性が成り立つこと
　・ 列に長期記憶があること

〔中略〕

要素の分布にスケールフリー性があることは，系の要素が無限に増えていく無限系であり，また，系は開放性を持つことを示唆する．一方，第二の基準の長期記憶に関しては，言語の列に内在する特性を表し，〔中略〕本書でいう長期記憶 (long memory) とは，コーパスのある部分が，そこから遠く離れた別の部分に影響を及ぼすことをいう．影響を及ぼす要因は，意味的，構文的，実用論的等さまざまで，その種別を問わず，長距離での関係をおしなべて長期記憶と総称する．日本語として認知科学以外の分野では耳慣れないかもしれないが，大元の英語 long memory は，複雑系科学では頻出する．

　「スケールフリー性」にせよ「長期記憶」にせよ言語学で一般に用いられる用語ではない．しかし，このような概念を用いて説明されてきた自然界や人間界の多数の現象から，言語現象がそれほど隔たっているわけではない，という洞察が複雑系言語学の要点である．ただし，他の現象とまったく同じというわけではない．その差異を的確にとらえることができれば，言語を言語たらしめている本質が見えてくるのではないか．そのような期待がある．

　・ 田中 久美子　『言語とフラクタル --- 使用の集積の中にある偶然と必然』　東京大学出版会，2021年．

[ 固定リンク | 印刷用ページ ]

■ #4673. 言語の統計的必然性と偶然性 [chaos_theory][complex_system][computational_linguistics][statistics][zipfs_law]

　本ブログでは，言語と複雑系，カオス理論，フラクタルの関係について，complex_system や chaos_theory などの記事で紹介してきた．しかし，とても関心はあるものの，私の頭の理解が伴っていかない分野のようで，なかなか深入りできない．文系頭にももう少し理解しやすい形で，上記の分野（一般的には数量言語学）の本などがあればよいのになぁと思っていたところ，昨年，田中久美子（著）『言語とフラクタル --- 使用の集積の中にある偶然と必然』が出版された．読みたいと思いつつ積ん読していたのだが，ようやくページ開く機会を得た．おもしろい．
　なぜ私がこれまで深入りできなかったのか．その辺りの理由も，導入部から教えてくれていて，とても嬉しい（田中，pp. 10--11）．

複雑系科学は自然・社会的な系に適用されてきたが，言語を捉える探求は，その中でも亜流であり，限定的であるといわざるをえない．その主な理由としては，物理学的方法論の対象は広いとはいってもまず自然であり，結果は人の解釈に依存しないものを目指すことがある．一方，言語の研究は，人の解釈を前提とした単語や文を探究してきた．統計力学的な方法論は，意味や解釈をめぐって，言語とは相性がよいとはいえなかったのである．その中で，物理学出身の研究者が言語を探究した報告があちこちに散乱しており，それは言語の諸研究の側からは見えない．本書はそのような既存研究に多くを拠っている．

　とてもよく分かった．例えば Zipf's Law (cf. zipfs_law) という著名な語彙統計学上の法則ですら，突っ込んだ議論を読みたいと思えば，言語学から一歩外に出なければならない．多くの普通の言語学の徒にとって，なかなか手を出せないのである．
　では，なぜ私は，理解するのが難しいと分かっていながらも，言語と複雑系などとの関係に心ひかれるのだろうか．その辺りのモヤモヤしたところも，田中 (11) が解消してくれた．

言語データを解析すると，統計的言語普遍としての性質が普遍的に立ち現れる．この事実から，統計的言語普遍は，言語が生み出す神秘の一つのように捉えられてきた側面がある．しかし，本書でも見るように，その因果関係はおそらく逆であると思われる．言語が統計的普遍を生み出すというよりは，統計的な性質がまずあり，言語はおそらくその性質を前提として成立している．つまり，統計的言語普遍は，言語を実現する前提となっていると思われる．ならばこの統計的必然性は，単語や統語構造などといった言語の諸性質に影響を及ぼしているはずである．そして，統計的必然の中で言語がどのような特殊性を持っているかを理解することは，言語の本質を捉える一つの手立てとなると思われる．

　どこまでが言語の（統計的）必然なのかが分かれば，そこから逸脱したものこそが言語における偶然だと知れるだろう．そして，後者こそ，人間が言語に込めた意図を反映しているものである可能性が高い．田中 (5) は，このことを「Mallarmé の賽」として示している．

かつて，詩人 Stéphane Mallarmé が，詩作において「賽を投じる」ことに言及している〔中略〕．「賽の一投は偶然を決して廃さない」との Mallarmé のことばは，純粋な統計としては自明なだけであるが，言語や詩作についてとなると難しい．言葉が発せられる背景には意図があることが多く，偶然だけに基づくとは考えにくい．Mallarmé は，言葉を使うことも，賽を投じるように偶然性を廃さないことを暗示し，偶然性をふまえた言葉のアートを試行したかにみえる．意図があって発話する場合にも，文や単語を生成する時に偶然が排除できないなら，言語行為には偶然性と必然性が混ざっているだろう．言語の統計的特性を知ることで，言葉が前提とする偶然性について明らかになる．その残滓の中に，意図など人間の要因の本質がかすかに見えはしまいか．

　私自身がなぜ言語の統計学に惹かれているのか，その辺りが読み進めるうちにどんどん分かってきたのが嬉しい．

　・ 田中 久美子　『言語とフラクタル --- 使用の集積の中にある偶然と必然』　東京大学出版会，2021年．

[ 固定リンク | 印刷用ページ ]

■ #3625. 地球史から学ぶ4つの視点 [historiography][methodology][complex_system]

　時間をかけて鎌田（著）『地球の歴史』の3巻本を読み終えた．人類史，世界史，日本史などをズームアウトした巨視的な視点でとらえるビッグ・ヒストリーがはやっているが，この地球史からみると，人類の歴史なり言語の歴史なりがいかに小さな話題かがわかる（「#751. 地球46億年のあゆみのなかでの人類と言語」 ([2011-05-18-1]) を参照）．ただし時間的に小さな話題ではあるが，その重要性を矮小化するわけではない．大きな視点に立つと見方が変わってくるということだ．
　著者は，第3巻の「長めのあとがき」で「地球科学特有のものの考え方，視座がある」 (255) として4点を挙げている．

　(1) 科学的ホーリズム (Holism)
　(2) 長尺の目
　(3) 歴史の不可逆性
　(4) 現場主義，または「百聞は一見に如かず」

　これらの点は，同じ歴史を扱う学問としての英語史にとっても示唆的である．(1) は，様々な現象が複雑に絡み合う複雑系の地球を理解するためには，その複雑な全体を1つのシステムとして理解する発想が不可欠だということだ．地球とは，生物学，数学はもとより歴史学，経済学などあらゆる学問を動員しなければ理解できない代物である，ということを述べている．
　(2) について，著者は「要素還元主義で未来予測を行うと，近視眼的な結論しか出ない事が多い．それに対して何万年，何千万年というスケールで捉えることにより，長期的な予測が可能となる．『過去は未来を解く鍵』というキーフレーズの拠りどころは，こうした長尺の目にある」 (257) とコメントしている．時代を前後に大きく飛び越えた視点が大切なのだ．
　(3) について，著者の言を以下に引用しよう (258) ．英語史にもほぼそのまま当てはまる．

そもそも不可逆な現象を多数扱うものだから，理論の通りに進行することが少ない．言い換えれば地球科学は「例外にあふれている」という特徴を持つ．地球の歴史には思わぬ事件が多数登場するが，われわれ地球科学者は起きた現象をできるだけ正確に記述しようとする．十九世紀以来の地質学の蓄積によって，記述と体系化はかなりできるようになった．しかし，それがなぜ起きたのかという根源的な質問に答えられる場合は，実に少ない．

　このような特徴ゆえに，地球科学は「例外や想定外に出会ってもうろたえない」「知的な強靱さ」 (259) を持ち合わせているという．これは嬉しい言葉だ．
　(4) は，五感に近いところで研究を進めるべしという原則である．
　歴史科学全般について，この4点から学べることは多い．

　・ 鎌田 浩毅　『地球の歴史（上・中・下巻）』　中央公論新社〈中公新書〉，2016年．

[ 固定リンク | 印刷用ページ ]

■ #3186. 1/f ゆらぎを悟っていた宮本武蔵 [1/f][dynamic_equilibrium][chaos_theory][complex_system]

　年明けから，語変化への適用可能性を求めて「#3171. 1/f ゆらぎ」 ([2018-01-01-1]) や動的平衡 (dynamic_equilibrium) の周辺について読書しているが，思いも掛けぬところで宮本武蔵に行き着いた．武者 (181--82) が指摘しているように，『五輪書』の水之巻「兵法心持の事」に次のようにある．

兵法の道におゐて，心の持ちやうは，常の心に替る事なかれ．常にも，兵法の時にも，少しもかはらずして，心を広く直にして，きつくひつぱらず，少しもたるまず，心のかたよらぬやうに，心をまん中におきて，心を静かにゆるがせて，其ゆるぎのせつなも，ゆるぎやまぬやうに，能能吟味すべし．静かなる時も心は静かならず，何とはやき時も心は少しもはやからず，心は躰につれず，躰は心につれず，心に用心して，身には用心をせず，心のたらぬ事なくして，心を少しもあまらせず，うへの心はよはくとも，そこの心をつよく，心を人に見わけられざるやうにして，小身なるものは心に大きなる事を残らずしり，大身なるものは心にちひさき事を能くしりて，大身も小身も，心を直にして，我身のひいきをせざるやうに心をもつ事肝要也．心の内にごらず，広くして，ひろき所へ智恵を置くべき也．智恵も心もひたとみがく事專也．智恵をとぎ，天下の理非をわきまへ，物毎の善悪をしり，よろづの芸能，其道〱をわたり，世間の人にすこしもだまされざるやうにして後，兵法の智恵となる心也．兵法の智恵において，とりわきちがふ事有るもの也．戦の場万事せはしき時なりとも，兵法の道理をきはめ，うごきなき心，能能吟味すべし．（宮本武蔵，p. 92）

　なるほど，心を常に中心に置きつつ揺るがせておくことによって，予測不能の状況に臨機応変に対応できるよう準備しておくというわけだ．武蔵は 1/f を体得し，動的平衡の奥義を究めていたことになろうか．
　言語からだいぶん離れてしまったが，ゆらぎや動的平衡のポイントが明確になってきた．常に不安定であるからこそ得られる安定，混沌のなかの秩序，動的な静態．これらのオクシモロンは言語においても成立にするに違いない．

　・ 武者 利光　『ゆらぎの発想　1/f ゆらぎの謎にせまる』　日本放送出版協会，1994年．
　・ 宮本 武蔵（著）・鎌田 茂雄（訳）　『五輪書』　講談社，1986年．

[ 固定リンク | 印刷用ページ ]

■ #3176. 言語とは動的平衡にあるシステムか？ (1) [dynamic_equilibrium][linguistics][entropy][language_change][chaos_theory][complex_system][1/f]

　福岡伸一氏のいう動的平衡 (dynamic_equilibrium) は，生命現象を説明する原理として画期的なものであるにとどまらず，もしかすると言語現象にも応用できるものかもしれない．動的平衡については「#3171. 1/f ゆらぎ」 ([2018-01-01-1]) の記事で簡単に触れたが，今回はその考え方に迫ってみよう．福岡 (261--63) の勢いのある文章を引くのが最も適切だろう．

　生体を構成している分子は，すべて高速で分解され，食物として摂取した分子と置き換えられている．身体のあらゆる組織や細胞の中身はこうして常に作り変えられ，更新され続けているのである．
　だから，私たちの身体は分子的な実体としては，数ヶ月前の自分とはまったく別物になっている．分子は環境からやってきて，いっとき，淀みとして私たちを作り出し，次の瞬間にはまた環境へと解き放たれていく．
　つまり，環境は常に私たちの身体の中を通り抜けている．いや「通り抜ける」という表現も正確ではない．なぜなら，そこには分子が「通り過ぎる」べき容れ物があったわけではなく，ここで容れ物と呼んでいる私たちの身体自体も「通り過ぎつつある」分子が，一次的に形作っているにすぎないからである．
　つまり，そこにあるのは，流れそのものでしかない．その流れの中で，私たちの身体は変わりつつ，かろうじて一定の状態を保っている．その流れ自体が「生きている」ということなのである．シェーンハイマーは，この生命の特異的なありようをダイナミック・ステイト（動的な状態）と呼んだ．私はこの概念をさらに拡張し，生命の均衡の重要性をより強調するため「動的平衡」と訳したい．英語で示せば dynamic equilibrium （equi=等しい， librium=天秤）となる．
　ここで私たちは改めて「生命とは何か？」という問いに答えることができる．「生命とは動的平衡にあるシステムである」という回答である．
　そして，ここにはもう一つの重要な啓示がある．それは可変的でサスティナブルを特徴とする生命というシステムは，その物質的構造基盤，つまり構成分子そのものに依存しているのではなく，その流れがもたらす「効果」であるということだ．生命現象とは構造ではなく「効果」なのである．
　サスティナブルであることを考えるとき，これは多くのことを示唆してくれる．サスティナブルなものは常に動いている．その動きは「流れ」，もしくは環境との大循環の輪の中にある．サスティナブルは流れながらも，環境とのあいだに一定の平衡状態を保っている．
　一輪車に乗ってバランスを保つときのように，むしろ小刻みに動いているからこそ，平衡を維持できるのだ．サスティナブルは，動きながら常に分解と再生を繰り返し，自分を作り替えている．それゆえに環境の変化に適用でき，また自分の傷を癒やすことができる．
　このように考えると，サスティナブルであることとは，何かを物質的・制度的に保存したり，死守したりすることではないのがおのずと知れる．
　サスティナブルなものは，一見，不変のように見えて，実は常に動きながら平衡を保ち，かつわずかながら変化し続けている．その軌跡と運動のあり方を，ずっと後になって「進化」と呼べることに，私たちは気づくのだ．

　上の文章の「生命」や「生体」を「言語」と置き換え，その他の用語も適切に言語的に読み替えても，おおかた理解できるように思われる．言語も常に変化し続けながらも平衡状態を保っているサスティナブルなシステムであり，静的な構造というよりは動的な「効果」としてみるのが妥当ではないかと．
　常に変化していることこそが，むしろ安定に貢献するという一見したところ逆説的に思われる見解は，動的平衡という用語を出さずとも，近年では複雑系 (complex_system)，カオス理論 (chaos_theory)，1/f ゆらぎ (1/f) との関連で指摘されている．本ブログでも，「#3122. 言語体系は「カオスの辺縁」にある」 ([2017-11-13-1])，「#3142. ホメオカオス (1)」 ([2017-12-03-1])，「#3143. ホメオカオス (2)」 ([2017-12-04-1])，「#3171. 1/f ゆらぎ」 ([2018-01-01-1]) などで触れてきたので，そちらも参照されたい．
　もう1つ，動的平衡とエントロピー (entropy) の関係について，福岡 (276--77) の説明を引用しておこう．

　秩序あるものはすべて乱雑さが増大する方向に不可避的に進み，その秩序はやがて失われいく．ここで私が言う「秩序」は「美」あるいは「システム」と言い換えてもよい．すべては，摩耗し，酸化し，ミスが蓄積し，やがて障害が起こる．つまりエントロピーは常に増大するのである．
　生命はそのことをあらかじめ織り込み，一つの準備をした．エントロピー増大の法則に先回りして，自らを壊し，そして再構築するという自転車操業的なあり方，つまりそれが「動的平衡」である．
　しかし，長い間，「エントロピー増大の法則」と追いかけっこしているうちに少しずつ分子レベルで損傷が蓄積し，やがてエントロピーの増大に追い抜かれてしまう．つまり秩序が保てない時が必ず来る．それが個体の死である．
　ただ，その時にはすでに自転車操業は次の世代にバトンタッチされ，全体としては生命活動が続く．現に生命はこうして地球上に三八億年にわたって連綿と維持され続けてきた．だから個体がいつか必ず死ぬというのは本質的には利他的なあり方なのである．
　生命は自分の個体を生存させることに関してはエゴイスティックに見えるけれど，すべての生物は必ず死ぬ．これによって致命的な秩序の崩壊が起こる前に，秩序は別の個体に移行し，リセットされる．実に利他的なシステムなのである．
　したがって「生きている」とは「動的平衡」によって「エントロピー増大の法則」と折り合いをつけているということである．換言すれば，時間の流れにいたずらに抗するのではなく，それを受け入れながら，共存する方法を採用している．

　言語も，秩序あるシステムとして存続するために「自らを壊し，そして再構築するという自転車操業的なあり方」を採用していると考えられるだろうか．

　・ 福岡 伸一　『新版　動的平衡　生命はなぜそこに宿るのか』　小学館〈小学館新書〉，2016年．

[ 固定リンク | 印刷用ページ ]

■ #3171. 1/f 繧?繧峨℃ [language_change][variation][chaos_theory][invisible_hand][complex_system][lexical_diffusion][speed_of_change][1/f][dynamic_equilibrium]

　2018年となりました．本年も hellog を続けていきます．よろしくお願い致します．
　新年最初の話題は「ゆらぎ」について．自然界に存在するゆらぎには規則的といえるものもあれば，まったく予想不可能なものもあるが，多くの現象においては，完全とはいえずとももある程度予測できるゆらぎが確認される．なかでも「1/f ゆらぎ」として知られているものは，身の回りにも数多く確認され，とりわけ人間が快を感じるもののなかにしばしば含まれていると言われる．そよ風，小川のせせらぎ，木漏れ日，木目や年輪，虫の羽音，岩塩の旨み，電車の揺れ，古い町並み，日本庭園，畳の目，手拍子，太鼓のリズム，噺家の声，バッハやモーツァルトの楽曲などにみられるほか，宇宙線強度，細胞構造，心拍周期にも認められるという．「1/f ゆらぎ」という呼称は，対象のゆらぎの周波数 (frequency) を成分分析し，各成分の強さを数学的操作を加えてグラフ化すると，右下がりの相関直線が得られることによる．1/f² や 1/f^-1 でもなく 1/f であるところが，どうやら人間にとっての快のポイントらしい（武者，pp. 24--39）．
　1/f ゆらぎが人間の生活に密接なところに多いというのは，言語（体系）にもみられる可能性があることを示唆する．ここで言語にとってゆらぎとは何かが問題になる．形式的な variation を想定することもできそうだし，言語変化 (language_change) の頻度 (frequency) や速度 (speed_of_language_change) などにも見られるかもしれない．例えば，1/f ゆらぎが語彙拡散 (lexical_diffusion) と関わっていたらおもしろそうだ．
　1/f ゆらぎは，複雑系 (complex_system) やカオス理論 (chaos_theory) とも深く関係する．言語体系が複雑系であり，言語変化がカオス理論の適用の対象となりうることは，「#3112. カオス理論と言語変化 (2)」 ([2017-11-03-1])，「#3122. 言語体系は「カオスの辺縁」にある」 ([2017-11-13-1])，「#3142. ホメオカオス (1)」 ([2017-12-03-1])，「#3143. ホメオカオス (2)」 ([2017-12-04-1]) などで触れてきた．そうだとすれば，1/f ゆらぎもまた言語に関与している可能性が高い．いずれの考え方にも共通しているのは，常に動いていて不安定なシステムこそ，周囲の予期できない変動に適応しやすいという点だ．不安定から安定が，混沌から秩序が生まれるようなシステムである．逆説的な言い方だが，そこには「動的な安定感」があるといってよい．あるいは最近の科学のキーワードでいえば「動的平衡」 (dynamic_equilibrium) である．「遊び」にも通じるものがある．
　この点と関連して，武者 (127--28) は 1/f ゆらぎを示す，目の焦点についての興味深い事例を紹介している．

目は物体の後ろ側に焦点を合わせています．そして焦点は，ピタッと一定のところに止まっているのではなく，いつも前後にふらふらと動いているのだそうです．
　この動きが，1/f ゆらぎに非常に近いのです．
　焦点が前にいったり後ろにいったり，ちょこちょこと絶えず動いているのは，動いているほうが，ものの位置が変わったときにすぐ焦点を合わせ直しやすいからです．テニスの選手がサーブを受けるときに，足を少し開いて上体を左右に揺すっていますが，あれは止まっていると，ボールが飛んできたときに体がすぐに動かないからでしょう．目の焦点も同じことです．
　また焦点は，見ようとするものよりも遠方に合わせられているのが普通のようです．見ているものが動くと，焦点がズレて画像がぼやけますが，もし焦点が物体に合っていると，ものが手前に来ても遠方に行っても，像がぼやけるという点では同じことになります．しかし，これでは焦点を合わせ直すのに，前後どちらに焦点を移動させればよいのか，とっさの判断ができません．見ているものよりも，少し遠方に焦点が定まっていれば，ものが焦点からズレて遠方に動くとものの像がはっきりしてきますし，その逆に手前に動けば，ぼやけかたが激しくなります．それと同時に，焦点は少し遠くに合わせられているのではないでしょうか．だから焦点が前後にゆらいでいるほうが，ものごとの変化に対応しやすいということでしょう．

　言語体系も常にゆらいでいるからこそ，人間のコミュニケーション欲求の絶えざる変化に即応できる柔軟なシステムとなっているのかもしれない．1/f ゆらぎの言語への応用は未知数だが，今後関心を寄せていきたい．

　・ 武者 利光　『ゆらぎの発想　1/f ゆらぎの謎にせまる』　日本放送出版協会，1994年．

[ 固定リンク | 印刷用ページ ]

■ #3143. ホメオカオス (2) [chaos_theory][complex_system][language_change][variation]

　昨日の記事 ([2017-12-03-1]) の続編．金子・津田 (205) の定義によると，ホメオカオスとは「弱いがたくさんの変数の関係したカオスによる安定性機構」である．金子・津田 (205--06) は，ホメオカオスを生命という複雑系において説明しながら，次のように述べている．

生命はその「増殖」という性質により次第に相互作用が強くなる．そこで同じものの集団であってもカオスによって性質が分化を始め，多様性が生まれる．そうやってできた多様性はホモカオス状態として維持される．その状態ではカオス的遍歴により外界からの擾乱や入力に対して多様かつ柔軟な応答を行っている．

　上で用いられている「カオス的遍歴」も，複雑系の分野のジャーゴンである．金子（「多様性を生み出すカオス」『日経サイエンス』1994年5月号）はカオス的遍歴を次のように説明している（吉永，p. 163 より孫引き）．

例えば，全要素がほぼ二つのクラスターに分かれてそれぞれでほぼ引き込んで振動する状態を長く続けた後，ばらばらになり，それをしばらく続けた後で，またほとんど二個（ないし数個）のクラスターに秩序化し，またばらばらに……といったことを繰り返す．つまり，いくつかの秩序的な状態の間が乱れた状態を経由してスイッチしていくのである．

　言語においても「ホメオカオス」や「カオス的遍歴」は日常的に見られる．例えば，言語は文法的に屈折に依存する言語と語順に依存する言語という両極の間を揺れ動くものと考えることができる．そのシフトの途中段階で，揺らぎや乱れが見られるかもしれないが，ゆくゆくはそれなりに落ち着くものではないか．音韻体系においても，語彙体系においても，常に揺れ動くという意味で静的な秩序というものはあり得ないが，動的にバランスが保持されている．
　平均台の上で完全に静止していることは難しいが，左右の小刻みな揺れを利用してバランスをとり続けることは可能である．ときに揺れ幅がやや大きくなることもあるが，そのピンチを解消するために，逆側に思い切ってバランスを傾けることで，結果として再び安定状態に回帰することはある．直立不動の静止状態というもの理論的にはあり得るが，現実的にはあり得ない．否，その理論的可能性をも否定し，理論上ですら常に不安定で動的であることを前提とするのがホメオカオスである．

　・ 金子 邦彦，津田 一郎　『複雑系のカオス的シナリオ』　朝倉書店，1996年．
　・ 吉永 良正　『「複雑系」とは何か』　講談社〈講談社現代新書〉，1996年．

[ 固定リンク | 印刷用ページ ]

■ #3142. ホメオカオス (1) [chaos_theory][complex_system][language_change][variation]

　言語体系がカオスと自己組織化を特徴とする複雑系であることについて，以下の記事で取り上げてきた（cf. 「#3111. カオス理論と言語変化 (1)」 ([2017-11-02-1]) ，「#3112. カオス理論と言語変化 (2)」 ([2017-11-03-1])，「#3122. 言語体系は「カオスの辺縁」にある」 ([2017-11-13-1])，「#3123. カオスとフラクタル」 ([2017-11-14-1])，「#3130. 複雑系言語学」 ([2017-11-21-1])）．
　言語の変化と変異を研究対象にしていると，言語に関わる現象のあまりの複雑さに圧倒される．どのように考えても解きにくいと悟った時，複雑系にすがる動機が生れる．見れば見るほど無秩序のようにみえて，それでも間違いなく何らかの秩序はあると直感するとき，それは複雑系に違いないという発想になる．静的な中心の欠如，動的な安定性の存在，結果としてバランスの保たれるアンバランス，秩序のなかの変化と変異．このような相矛盾する特徴が，気象や物理現象や生物や言語といった一筋縄では理解できない対象のうちに内在する．
　『「複雑系」とは何か』を著わした吉永 (169) は，このような秩序を金子らに従って「ホメオカオス」という造語で呼んでいる．

部分秩序層で生成される秩序は，自己組織化という言葉から誤ってイメージされるような，静的な安定性ではない．多数の自由度をもつ弱いカオス的振動が，完全にそろうわけでもなく，かといって完全にばらばらになるわけでもなく，お互い影響し合い，依存し合いながら，つまり多様性を保持しながら――あるいは多様性をもつがゆえに――大筋ではあたかも基準となる状態があって，そこから逸脱しないかのようなふるまいをする，動的な安定状態である．

　金子らはこの多様性を維持した安定性機構を「ホメオカオス homeochaos」と呼んでいる．いわゆるホメオスタシスが，理想的な静的安定性を想定し，そこから生じたゆらぎに対するゆり戻しのフィードバック機構と考えられてきたのに対し，ホメオカオスはそのような理想状態を仮想しなくてもいいことを教えてくれている．

　さらに，このホメオカオスにおいて著しいのは，秩序の「次元」や「自由度」といった枠組みそのものが変化し，異なる枠組みへ飛躍することがあり得るということだ．これはオープンカオス（開放型カオス）と呼ばれる（吉永, pp. 169--70）．

　ホメオカオスがとくに重要になるのは，相空間の次元を決めるシステムそのものの自由度が変動するケースである．具体的には，要素的なユニットが互いの相互作用を経て分裂したり，また途中から消失したりする場合であり，たとえば細胞の増殖や死など，自然界の大半のシステムはこうした自由度の変動を許す開いたシステムになっている．
　自由度が固定された，したがって相空間の次元が不変に保たれた閉じたシステムに見られる通常のカオスでは，相空間の中での軌道が不安定になって伸ばされていくと，どこかで折りたたまれる．相空間そのものが変わることはない．ところが，自由度が変動する開いたシステムでは，不安定性が増大していって運動が不規則になると，そこで自由度のジャンプが起こることがある．そして，新たに出現した余分な自由度に不安定さが分配されると，そこで生じた大自由度の弱いカオス状態にホメオカオスの機構が働いて，多様性を維持した安定性が生成される．このような開いたシステムに特有なカオスのダイナミクスを金子らは「開放型カオス」と呼んでいる．

　システムをシステムとして維持するための動的な機構が提案されるのであれば，それは言語にも適用できる可能性が高いだろう．それくらい言語は動的で複雑である．

　・ 吉永 良正　『「複雑系」とは何か』　講談社〈講談社現代新書〉，1996年．
　・ 金子 邦彦，津田 一郎　『複雑系のカオス的シナリオ』　朝倉書店，1996年．

[ 固定リンク | 印刷用ページ ]

■ #3130. 複雑系言語学 [chaos_theory][complex_system][variety][zipfs_law][language_change][contact][methodology]

　Kretzschmar は，言語を複雑系としてとらえ，言語変化を論じる研究者である．最近の論文で，複雑系の概念を用いて，アメリカ英語の諸変種がいかにして生じてきたかという問題を論じている．論文の冒頭 (251) で，発話を複雑系としてとらえる見方が端的に述べられている．

. . . language in use, speech as opposed to linguistic systems as usually described by linguists, satisfies the conditions for complex systems as defined in sciences such as physics, evolutionary biology, and economics . . . .

　言語は複雑系とみなされるべき2つの特徴，すなわち "non-linear distribution" と "scaling" を備えているという (253) ．前者 "non-linear distribution" は，具体的にいえば，漸近双曲線 (A-curve) の分布を指している．例としてすぐに思い浮かぶのは，「#1103. GSL による Zipf's law の検証」 ([2012-05-04-1]) や「#1101. Zipf's law」 ([2012-05-02-1]) で紹介した zipfs_law のグラフである．少数の高頻度語と多数の低頻度語により，右下へ長い尾を引くグラフが描かれる．Kretzschmar は，言語に関わる他の現象でもこのようなグラフが得られると主張する．
　「言語＝複雑系」に関するもう1つの特徴である "scaling" は，A-curve のような分布が言語の異なるレベルにおいて繰り返し現われる状況を指している．アメリカ東部諸州における方言単語（訛語）の頻度調査で，各形態について頻度順位の高い順に並べて頻度をプロットしていくと A-curve となるが，New York 州に限って同様のグラフを作成しても類似した曲線が得られるし，女性話者に限ったグラフでもやはり同様の曲線が得られるという (255) ．
　グラフが非線形でありスケール・フリーということになれば，当然ながら「#3123. カオスとフラクタル」 ([2017-11-14-1]) が想起される．関連して，「#3111. カオス理論と言語変化 (1)」 ([2017-11-02-1])，「#3112. カオス理論と言語変化 (2)」 ([2017-11-03-1])，「#3122. 言語体系は「カオスの辺縁」にある」 ([2017-11-13-1]) も参照されたい．
　Kretzschmar (263--64) は論文の最後で，言語変種の生起・拡大を説明するのに複雑系の考え方が有用であると結論づけ，複雑系言語学を唱える．

Complexity science is the model that can cope successfully with the problems of language variation and change that we are interested in solving for the history of American English. Complexity science addresses the emergence of a new American variety, along with its component regional varieties, more adequately than traditional approaches. Complex systems replace the notion of monolithic "language contact" or Fischer's "cultural shift" with interaction between speakers. Complex systems can deal with the extension of existing varieties into new areas, and still account for the evident acquisition of new variants from important cultural groups in different areas. Finally, complex systems can cope with contemporary American cultural change and attendant language change, again without recourse to monolithic thinking. We are just at the beginning of research to understand the operation of the complex system of speech, but it is already clear that it gives us a good way to describe how the process of emergence and change really works.

　従来のような "monolithic" な言語接触に基づいた理論ではなく，それを内に含み込むような複雑系の理論こそが，これからの言語変化研究を支えていくのではないかというわけだ．確かに刺激的な話題である．

　・ Kretzschmar, William A., Jr. "Complex Systems in the History of American English." Chapter 4 of Developments in English: Expanding Electronic Evidence. Ed. Irma Taavitsainen, Merja Kytö, Claudia Claridge, and Jeremy Smith. Cambridge, 2015. 251--64.

[ 固定リンク | 印刷用ページ ]

■ #3123. カオスとフラクタル [chaos_theory][variation][lexical_diffusion][complex_system]

　「#3111. カオス理論と言語変化 (1)」 ([2017-11-02-1]) の記事で，初期条件の僅かな異なりが後に甚大な差異をもたらし得ることを，簡単な数式（ロジスティック方程式）により示した．このようなカオスは，ポーランド生まれの数学者 Benoît Mandelbrot (1924--2010) により幾何学と結びつけられ，自己相似的な図形「フラクタル」 (fractal) と関連づけられるようになった．
　数列がある数値に収斂していく様子を幾何学的に表現すれば，ある1点へすべてが集まっていく図形が想像されるだろう．これをアトラクタという．アトラクタには，このようにきわめて単純なものもあるが，もう少し複雑なものとして閉じた輪の形状を示すものもある．ここでは収斂してゆく先が1点ではなくループ状ではあるものの，まだ十分に規則的と呼びうるアトラクタである．しかし，1点でもループ状でもなく，より複雑な図形がアトラクタとなるケースがある．これがまさにカオスの示すアトラクタであり，その本質が解明されていないことから，ストレンジ・アトラクタと呼ばれる（先の記事で示したローレンツ・アトラクタがその1例）．このようなアトラクタを，別の幾何学的な演算を加えた上で描きなおすと，非常に複雑だが，美しい自己相似的な図形，つまりフラクタルとなるものがある．その最も有名な例が，「マンデルブロー集合」 (Mandelbrot set) である．その形状から "gingerbread man" とも呼ばれる．以下をクリックして，次々に拡大していくGIFアニメーションもどうぞ．



　この図形のある部分を拡大していくと，もとの図形と相似な図形が次々と現われる．この再帰性が永遠に続いていくのである．
　言語変化がカオス現象の1例だとすれば，それに対応する幾何学図形であるフラクタルとその自己相似性という特徴は，言語変化のいかなる側面を表わしていると考えられるのだろうか．
　フラクタルの自己相似性は，とりわけカオスの辺縁においてみられる．例えば，言語変化における variation に関して，あらゆる側面・次元で似たようなことが生じている，というようなことが考えられようか．語彙拡散のS字曲線が複数のより小さなS字曲線から成っているという事実も，フラクタル的である．
　カオスとフラクタルの不思議な関係については，スチュアート (268--301) が読みやすい．

　・ スチュアート，イアン（著），須田 不二夫・三村 和男（訳）　『カオス的世界像　非定形の理論から複雑系の科学へ』　白揚社，1998年．

[ 固定リンク | 印刷用ページ ]

■ #3122. 言語体系は「カオスの辺縁」にある [chaos_theory][language_change][invisible_hand][complex_system]

　『カオス的世界像』の著者スチュアート (481--82) によると，カオスについて興味深いことは，カオスと秩序との境目に近い「カオスの辺縁」において，ただならぬ何かが起こっているということである．

　複雑性はカオスの概念の上に築かれるものである．実際，複雑性理論にうるさくつきまとう基本語――あるいはより正確には慣用句――は「カオスのふち（辺縁）」という語句である．カチカチと規則正しく時を刻む，歯車でできた時計仕掛の宇宙のように，いくつかのシステムは非常に単純な仕方でふるまう．しかし，カオス現象を示すシステムはもっとずっと複雑な仕方でふるまう．その極端な例として，気体分子の全体としてのランダムな運動がある．その中間にあるシステムは，もっと興味深い類のふるまい――複雑ではあるがパターンを暗示するようなふるまい――を示す．これらの複雑ではあるが組織化されたシステムは，まさに秩序とカオスの間の遷移状態にあるように見える――そして，それこそが「カオスの辺縁」なのである．ここで示唆されるのは，淘汰（選択）あるいは学習によってシステムがこの境域に行きつくということである．あまりに単純なシステムは，競合的環境のなかでは生き残れない．なぜなら，より複雑微妙なシステムはそれらの規則性を食い物にすることによって単純なシステムを出し抜けるからである．（もしもある現金輸送会社の車が，毎週金曜日の午前十時に銀行からお金を受け取り，正確に同じルートを通って輸送するとしたら，強盗はいとも簡単に現金強奪劇を演ずることができるだろう．）まったくランダムなシステムもまた，生き残らないだろう．なぜならそういうシステムは，秩序のある（コヒーレントな）ことは何もなし遂げられないからである．（もしも現金輸送車がまったくランダムなルートをとるとしたら，銀行に到着するまでに時間があまりにかかりすぎ，到着する前にその仕事は別の会社に奪われてしまうだろう．）だから，生き残るという点では，全体としての構造を失ってしなわない程度にできるかぎり複雑化するのが利益になるのである．進化するシステムは，カオスの辺縁にとどまるよう強いられているのである．

　言語体系も，環境の変化に柔軟に適応する体系である．言語変異や言語接触は「カオスの辺縁」ととらえることができ，まさにそこで最もおもしろい現象が繰り広げられている．言語は，生き残りに成功してきた，単純すぎも複雑すぎもしない1つのシステムなのである．
　関連して，「#3111. カオス理論と言語変化 (1)」 ([2017-11-02-1])，「#3112. カオス理論と言語変化 (2)」 ([2017-11-03-1]) も参照．

　・ スチュアート，イアン（著），須田 不二夫・三村 和男（訳）　『カオス的世界像　非定形の理論から複雑系の科学へ』　白揚社，1998年．

[ 固定リンク | 印刷用ページ ]

■ #3112. カオス理論と言語変化 (2) [chaos_theory][language_change][teleology][invisible_hand][complex_system]

　昨日の記事 ([2017-11-02-1]) に引き続いての話題．カオス理論と言語変化の接点に注目した英語史研究者に Smith がいる．Smith (194) は，言語変化について次のように述べている．

Change . . . is the result of the complex interaction of extralinguistic and intralinguistic developments, and any resulting change itself interacts with further developments to produce yet more change. The conception is therefore a dynamic one . . . .

　Smith (195) は，上のように述べた後で，このような多様な側面をもつ言語変化を「カオス理論」で説明され得る現象として提示している．

   Such a multifarious conception of language change . . . seems to correspond to the most recent paradigm in both the natural and human sciences: 'chaos-theory'. Chaos-theory is really about order, about the way in which order results from complex interaction. The best-known popular example of this process --- the butterfly stamping in the forest causing a storm a thousand miles away --- is really about how a tiny innovation can make a difference, by interacting with other innovations to produce a snowball effect. If language is a metastable system deployed by interacting innovative and conservative language-users, it does not, in a chaotic world, require or imply some divine plan or overall grand design. Rather, living languages are the result of what Dawkins has called a 'blind watchmaker' effect, whereby order comes out of chaos.
   Such an approach is hardly revolutionary, and . . . no claims of special newness are made here.

　Smith は，言語変化を，言語に関与する種々の要素の "complex interaction" のたまものとしてとらえている．Smith の言語変化観については，「#1123. 言語変化の原因と歴史言語学」 ([2012-05-24-1])，「#1466. Smith による言語変化の3段階と3機構」 ([2013-05-02-1])，「#1928. Smith による言語レベルの階層モデルと動的モデル」 ([2014-08-07-1]) を参照．上の引用にもある "blind watchmaker" の比喩と関連して，teleology や invisible_hand の記事もどうぞ．

　・ Smith, Jeremy J. An Historical Study of English: Function, Form and Change. London: Routledge, 1996.

[ 固定リンク | 印刷用ページ ]

■ #3111. カオス理論と言語変化 (1) [chaos_theory][language_change][complex_system]

　1960年代より，カオス理論 (chaos_theory) は「時計じかけの宇宙」観に代わる自然科学のパラダイムとして受け入れられてきたのみならず，社会科学その他の領域へも応用されてきた．それは，気象学，物理学，天文学，数学に始まり，生物学，経済学，社会学にまで裾野を広げている．例えば，気象現象，流体力学，幾何学，生物の個体数の増加速度，立ち上る煙の振る舞い，綿花の価格などがカオス理論で説明されるといわれ，ほかには実用的なところでCGの描画にも活用されている．
　カオス理論は，その名前とは裏腹に，実は秩序に関する理論である．一見ランダムで予測できない現象にも，ある種の傾向が見られると主張する．また，カオス理論は，初期条件が僅かに異なるだけでも，その後の振る舞いに甚大な影響が及ぼされる点を指摘する．その最も有名な例がバタフライ効果 (butterfly effect) だろう．『サイエンス大図鑑　コンパクト版』 (351) によれば，バタフライ効果とは，

カオス系の主な特徴である「初期条件に大きく左右される性質」を表現するために，エドワード・ローレンツが考案した用語．初期条件の変更がたとえわずかであっても，現象が何度も繰り返されるうちに，大きな差が生じてしまうことを示す．ローレンツは「蝶（バタフライ）がブラジルで羽ばたくと，テキサスで竜巻が起こる」と表現した．彼のデータから描かれたモデル“ローレンツ・アトラクタ”は，偶然にも蝶の形をしている．カオス的な現象の進行を示すこのモデルでは，突然，進行方向が逆転し，同じ軌跡は2度と通らない．

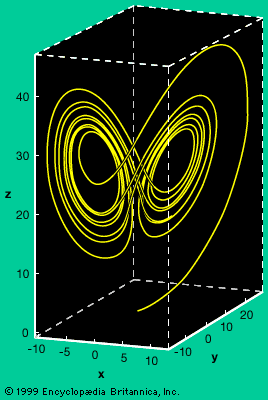
　"Lorenz' attractor" と呼ばれる蝶を彷彿とさせるこの3次元のグラフは，天候の軌跡を表現している．開始点の座標がたとえ僅かでも異なると，軌道が大きく逸脱し，異なる羽形の領域（各々穏やかな天候と荒れた天候を表わす）へ帰着するという．
　初期条件の僅かな異なりが後に甚大な差異をもたらす現象を，数学の簡単な例で確かめることができる．A を定数（ここでは A = 2 とおく）とし，x₀ を0から1の間をとるものとする（ここでは x₀ = 0.9 とおく）．このとき，x₁ を Ax₀(1 - x₀) と定義すれば，x₁ = 2 * 0.9 * (1 - 0.9) = 0.18 となる．同様に，x₂ = Ax₁(1 - x₁) = 2 * 0.18 * (1 - 0.18) = 0.2952 とし，このサイクルを繰り返して，x₀ から x_n までの数列を得る．結果は，0.09, 0.18, 0.2952, 0.4161, 0.4859, 0.4996, 0.5000, 0.5000, ... となり，0.5000で安定する．A の値を2から3まで大きくしても，安定期に入るまでのサイクル数は増えるものの，最終的には安定する．これは，振り子が多少乱されても，最終的には揺れが安定してくることになぞらえられる．
　ところが，A が3を超えると，2つの数を行き来する関係に至るなど予期できない振る舞いを示すようになる．そして，A が3.57程度になると，いつまでたっても定期性を示さない状態，すなわちカオスの状態に帰結する．例えば，A を3.7とおき，初期値の x₀ を 0.9 と置いた場合と，僅かに異なる 0.9000009 と置いた場合の数列を得てグラフをプロットすると，以下のように興味深い結果が得られる．



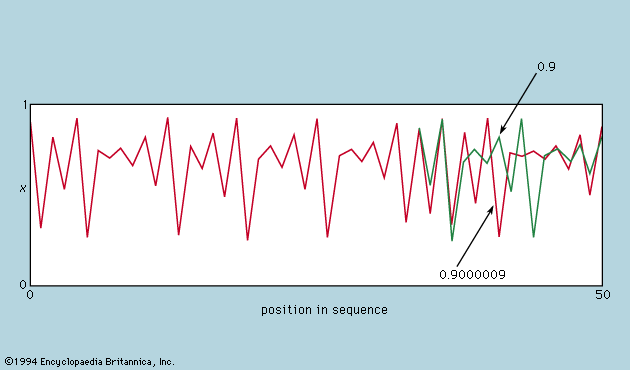
　35サイクルまでは2つのグラフは事実上重なっているが，以降40サイクルくらいまでにある種の安定的な分岐を示すようになり，その後は互いに無関係のカオス的な様相を呈する．すべては，初期値の僅かな差に由来するのだ．見方を変えれば，種々の初期条件がほぼ一致していたとしても，ある1つの条件において0.000009ほどの差があれば，後にたどる運命を天と地ほどまで違えるのに十分であるということになる．
　カオス理論は，「環境」が関与するありとあらゆる分野に適用されることが明らかになってきている．言語とその変化も「環境」のなかで作用しているものであるから，当然，カオス理論と無縁ではない．例えば，拙著『英語の「なぜ？」に答える　はじめての英語史』の「3.5.2 -e の衰退の一波万波」で示したとおり，英語史における屈折語尾の弱化という調音の僅かな変化が引き金となって，英語の統語論ががらんと組み替えられた事例が，カオス理論のバタフライ効果に対応するだろうか．言語も，「一波動けば万波生ず」なのである．
　明日の記事でも，引き続きカオス理論の話題を扱う．

　・ デイヴィス，アダム・ハート（総監修），日暮 雅通（監訳）　『サイエンス大図鑑　コンパクト版』　河出書房新社，2014年．
　・ 堀田 隆一　『英語の「なぜ？」に答えるはじめての英語史』　研究社，2016年．

[ 固定リンク | 印刷用ページ ]