hellog〜英語史ブログ / 2015-08-21
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
2015-08-21 Fri
■ #2307. 綴字の余剰性 (2) [spelling][redundancy][statistics][information_theory][alphabet][final_e][silent_letter]
「#2249. 綴字の余剰性」 ([2015-06-24-1]) で取り上げた話題.別の観点から英語綴字の余剰性を考えてみよう.
Roman alphabet のような単音文字体系にあっては,1文字と1音素が対応するのが原理的に望ましい.しかし,言語的,歴史的,その他の事情で,この理想はまず実現されないといってよい.現実は理想の1対1から逸脱しているのだが,では,具体的にはどの程度逸脱しているのだろうか.
ここで,「#1159. MRC Psycholinguistic Database Search」 ([2012-06-29-1]) を利用して,文字と音素の対応の度合いをおよそ計測してみることができる.もし理想通りの単音文字体系であれば,単語の綴字を構成する文字数と,その発音を構成する音素数は一致するだろう.英語語彙を構成する各単語について,文字数と音素数の比を求め,その全体の平均値などの統計値を出せば,具体的な指標が得られるはずだ.綴字が余剰的 (redundancy) であるということはこれまでの議論からも予想されるところではあるが,具体的に,文字数対音素数の比は,2:1 程度なのか 3:1 程度なのか,どうなのだろうか.
まずは,MRC Psycholinguistic Database Search を以下のように検索して,単語ごとの,文字数,音素数,両者の比(=余剰性の指標)の一覧を得る(SQL文の where 以下は,雑音を排除するための条件指定).
select WORD, NLET, NPHON, NLET/NPHON as REDUNDANCY, PHON from mrc2 where NPHON != "00" and WORD != "" and PHON != "";
この一覧をもとに,各種の統計値を計算すればよい.文字数と音素数の比の平均値は,1.192025 だった.比を0.2刻みにとった度数分布図を示そう.
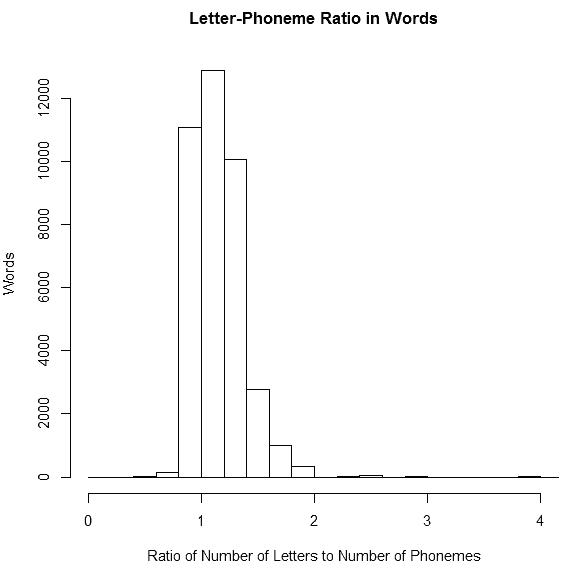
文字数別に比の平均値をとってみると,興味深いことに3文字以下の単語では余剰性は 1.166174 にとどまり,全体の平均値より小さくなる.一方,4文字から7文字までの単語では平均より高い 1.231737 という値を示す.8文字以上になると再び余剰性は小さくなり,1.157689 となる.文字数で数えて中間程度の長さの単語で余剰性が高く,短い単語と長い単語ではむしろ相対的に余剰性が低いようだ.この理由については詳しく分析していないが,「#1160. MRC Psychological Database より各種統計を視覚化」 ([2012-06-30-1]) でみたように,英単語で最も多い構成が8文字,6音素であるということや,final_e をはじめとする黙字 (silent_letter) の分布と何らかの関係があるかもしれない.
さて,全体の平均値 1.192025 で示される余剰性の程度がどれくらいのものなのか,ほかに比較対象がないので評価にしにくいが,主観的にいえば理想の値 1.0 から案外と隔たっていないなという印象である.英単語における文字と音素の関係は,「#2292. 綴字と発音はロープでつながれた2艘のボート」 ([2015-08-06-1]) の比喩でいえば,そこそこよく張られた短めのロープで結ばれた関係ともいえるのではないか.
ただし,今回の数値について注意すべきは,英単語における文字と音素の対応を一つひとつ照らし合わせてはじき出したものではなく,本来はもっと複雑に対応するはずの両者の関係を,それぞれの長さという数値に落とし込んで比を取ったものにすぎないということだ.最終的に求めたい綴字の余剰性そのものではなく,それをある観点から示唆する指標といったほうがよいだろう.それでも,目安となるには違いない.
2026 : 01 02 03 04 05 06 07 08 09 10 11 12
2025 : 01 02 03 04 05 06 07 08 09 10 11 12
2024 : 01 02 03 04 05 06 07 08 09 10 11 12
2023 : 01 02 03 04 05 06 07 08 09 10 11 12
2022 : 01 02 03 04 05 06 07 08 09 10 11 12
2021 : 01 02 03 04 05 06 07 08 09 10 11 12
2020 : 01 02 03 04 05 06 07 08 09 10 11 12
2019 : 01 02 03 04 05 06 07 08 09 10 11 12
2018 : 01 02 03 04 05 06 07 08 09 10 11 12
2017 : 01 02 03 04 05 06 07 08 09 10 11 12
2016 : 01 02 03 04 05 06 07 08 09 10 11 12
2015 : 01 02 03 04 05 06 07 08 09 10 11 12
2014 : 01 02 03 04 05 06 07 08 09 10 11 12
2013 : 01 02 03 04 05 06 07 08 09 10 11 12
2012 : 01 02 03 04 05 06 07 08 09 10 11 12
2011 : 01 02 03 04 05 06 07 08 09 10 11 12
2010 : 01 02 03 04 05 06 07 08 09 10 11 12
2009 : 01 02 03 04 05 06 07 08 09 10 11 12
最終更新時間: 2026-02-21 08:56
Powered by WinChalow1.0rc4 based on chalow