hellog〜英語史ブログ / 2013-08-06
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
2013-08-06 Tue
■ #1562. 韻律音韻論からみる yod-dropping [phonetics][phonology][diphthong][vowel][syllable][metrical_phonology][variation][yod-dropping]
現代英語には /juː/ という上昇2重母音 (rising diphthong) がある.英語変種によっても異なるが,この2重母音にはいくつかの特徴がある.そのうちの共時的な変異と通時的な変化に関わる特徴として,「#841. yod-dropping」 ([2011-08-16-1]) がある.時に /juː/ から /j/ が脱落し,/uː/ として実現される音韻過程のことだ.
現在進行中の yod-dropping を記述・説明するのに,Hogg and McCully (42--45) で述べられている metrical phonology (韻律音韻論)による分析が利用できるかもしれないと思ったので,紹介しておきたい.子音 X + /juː/ からなる音節は,下図の左の基底構造をもっていると分析される.
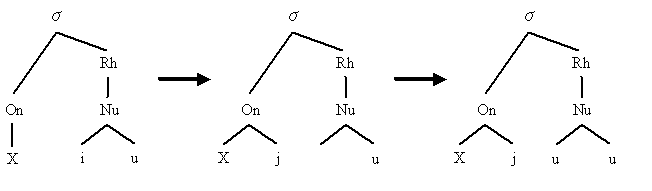
次に,この基底構造の Nucleus における /i/ が,/j/ として Onset へ移動すると想定する.引き続き,/i/ が移動したことによって空いた Nucleus の第1の位置に,後続の /u/ のコピーが作り出される.
このように分析する利点はいくつかある.まず,基底構造の Onset に /Xj/ を想定してしまうと,cue /kjuː/, few /fjuː/ などでは問題ないが,new /njuː/, lewd /ljuː/ などでは問題が生じる.なぜならば2モーラからなる Onset において第1モーラの聞こえ度は無声摩擦音と同等かそれ以下でないといけないという一般的な制限があるからである.この制限に従えば,/n/ や /l/ は聞こえ度が高すぎるために,Onset の第1モーラとなることはできないはずだ.しかし,実際には第1モーラになっているので,これは例外的に派生したものとして分析する必要があることになる.
また,この分析は /Xj/ の後には長母音しか生起し得ないことと符合する.というのは,Nucleus の第2モーラには /i/ か /u/ しか起こり得ず,それが前位置にコピーされることをこの分析は要求しているからである.
さらに,clue, drew, threw など,もともと Onset が2モーラ(2子音結合)からなる場合には,/j/ が左へ移動してゆくための空きスペースがないために,/j/ 自身が最終的に脱落してしまうと説明することができる.つまり,子音連続の直後の yod-dropping が必須であることをうまく説明する.
変異としての yod-dropping は,英語変種によっても異なるが,dew, enthuse, lewd, new, suit, tune などの語における /j/ の有無の揺れによって示される.共時的にも通時的にも,yod-dropping の起こりやすさは先行する子音 X が何であるかによってある程度は決まることが知られているが,これをいかに上の分析に組み込むことができるかが次の課題となるだろう.
・ Hogg, Richard and C. B. McCully. Metrical Phonology: A Coursebook. Cambridge: CUP, 1987.
2026 : 01 02 03 04 05 06 07 08 09 10 11 12
2025 : 01 02 03 04 05 06 07 08 09 10 11 12
2024 : 01 02 03 04 05 06 07 08 09 10 11 12
2023 : 01 02 03 04 05 06 07 08 09 10 11 12
2022 : 01 02 03 04 05 06 07 08 09 10 11 12
2021 : 01 02 03 04 05 06 07 08 09 10 11 12
2020 : 01 02 03 04 05 06 07 08 09 10 11 12
2019 : 01 02 03 04 05 06 07 08 09 10 11 12
2018 : 01 02 03 04 05 06 07 08 09 10 11 12
2017 : 01 02 03 04 05 06 07 08 09 10 11 12
2016 : 01 02 03 04 05 06 07 08 09 10 11 12
2015 : 01 02 03 04 05 06 07 08 09 10 11 12
2014 : 01 02 03 04 05 06 07 08 09 10 11 12
2013 : 01 02 03 04 05 06 07 08 09 10 11 12
2012 : 01 02 03 04 05 06 07 08 09 10 11 12
2011 : 01 02 03 04 05 06 07 08 09 10 11 12
2010 : 01 02 03 04 05 06 07 08 09 10 11 12
2009 : 01 02 03 04 05 06 07 08 09 10 11 12
最終更新時間: 2026-02-21 08:56
Powered by WinChalow1.0rc4 based on chalow