logic - hellog〜英語史ブログ

■ #5661. 否定とは何か？ [negation][polarity][negative][terminology][syntax][double_negative][logic][assertion][semantics]

　昨日の記事「#5670. なぜ英語には単数形と複数形の区別があるの？ --- Mond での質問と回答より」 ([2024-10-24-1]) で，否定 (negation) の話題を最後に出しました．言語において否定とは何か．これはきわめて大きな問題です．論理学や哲学からも迫ることができますが，ここでは言語学の観点に絞ります．
　言語学の用語辞典に頼ることから始めましょう．まず Crystal (323--24) より引用します．

negation (n.) A process or construction in GRAMMATICAL and SEMANTIC analysis which typically expresses the contradiction of some or all of a sentence's meaning. In English grammar, it is expressed by the presence of the negative particle (neg, NEG) not or n't (the CONTRACTED negative); in LEXIS, there are several possible means, e.g. PREFIXES such as un-, non-, or words such as deny. Some LANGUAGES use more than one PARTICLE in a single CLAUSE to express negation (as in French ne . . . pas). The use of more than one negative form in the same clause (as in double negatives) is a characteristic of some English DIALECTS, e.g. I'm not unhappy (which is a STYLISTICALLY MARKED mode of assertion) and I've not done nothing (which is not acceptable in STANDARD English). . . .
   A topic of particular interest has been the range of sentence STRUCTURE affected by the position of a negative particle, e.g. I think John isn't coming v. I don't think John is coming: such variations in the SCOPE of negation affect the logical structure as well as the semantic analysis of the sentence. The opposite 'pole' to negative is POSITIVE (or AFFIRMATIVE), and the system of contrasts made by a language in this area is often referred to as POLARITY. Negative polarity items are those words or phrases which can appear only in a negative environment in a sentence, e.g. any in I haven't got any books. (cf. *I've got any books).

　次に Bussmann (323) を引用します．論理学における否定に対して言語学の否定を，次のように解説しています．

In contrast with logical negation, natural language negation functions not only as sentence negation, but also primarily as clausal or constituent negation: she did not pay (= negation of predication), No one paid anything (= negation of the subject NP), he paid nothing (= negation of the object NP). Here the scope (= semantic coverage) of negation is frequently polysemic or dependent on the placement of negation, on the sentence stress . . . as well as on the linguistic and/or extralinguistic context. Natural language negation may be realized in various ways: (a) lexically with adverbs and adverbial expressions (not, never, by no means), indefinite pronouns (nobody, nothing, none), coordinating conjunctions (neither . . . nor), sentence equivalents (no), or prepositions (without, besides); (b) morphologically with prefixes (in + exact, un + interested) or suffix (help + less); (c) intonationally with contrastive accent (in Jacob is not flying to New York tomorrow the negation can refer to Jacob, flying, New York, or tomorrow depending which elements are stressed); (d) idiomatically by expressions like For all I care, . . . . Formally, three types of negation are differentiated: (a) internal (= strong) negation, the basic type of natural language negation (e.g. The King of France is not bald); (b) external (= weak) negation, which corresponds to logical negation (e.g. It's not the case/it's not true that p); (c) contrastive (= local) negation, which can also be considered a pragmatic variant of strong negation to the degree that stress and the corresponding modifying clause are relevant to the scope of the negation (e.g. The King of France is not bald, but rather wears glasses. The linguistic description of negation has proven to be a difficult problem in all grammatical models owing to the complex interrelationship of syntactic, prosodic, semantic, and pragmatic aspects.

　この2つの解説に基づいて，言語学における否定に関する論点・観点を箇条書き整理すると次のようになるでしょうか．

1. 否定の種類と範囲
　・ 文否定 (sentence negation)
　・ 節否定 (clausal negation)
　・ 構成要素否定 (constituent negation)
2. 否定の実現様式
　・ 語彙的 (lexically): 副詞，不定代名詞，接続詞，前置詞など
　・ 形態的 (morphologically): 接頭辞，接尾辞
　・ 音声的 (intonationally): 対照アクセント
　・ 慣用的 (idiomatically): 特定の表現
3. 否定の形式的分類
　・ 内的（強い）否定 (internal/strong negation)
　・ 外的（弱い）否定 (external/weak negation)
　・ 対照的（局所的）否定 (contrastive/local negation)
4. 否定の作用域 (scope)
　・ 否定辞の位置による影響
　・ 文強勢による影響
　・ 言語的・非言語的文脈による影響
5. 2重否定 (double negative)
　・ 方言や非標準英語での使用
　・ 文体的に有標な肯定表現としての使用
6. 極性 (polarity)
　・ 肯定 (positive/affirmative) vs. 否定 (negative)
　・ 否定極性項目
7. 否定に関する統語的，韻律的，意味的，語用論的側面の複雑な相互関係
8. 自然言語の否定と論理学的否定の違い

この一覧は，否定の複雑さと多面性を示しています．案の定，抜き差しならない問題です．

　・ Crystal, David, ed. A Dictionary of Linguistics and Phonetics. 6th ed. Malden, MA: Blackwell, 2008. 295--96.
　・ Bussmann, Hadumod. Routledge Dictionary of Language and Linguistics. Trans. and ed. Gregory Trauth and Kerstin Kazzizi. London: Routledge, 1996.

[ 固定リンク | 印刷用ページ ]

■ #5458. 理論により異なる主語の捉え方 [subject][terminology][semantics][syntax][logic][case][generative_grammar]

　昨日の記事「#5457. 主語をめぐる論点」 ([2024-04-05-1]) に続き，別の言語学用語辞典からも主語 (subject) の項目を覗いてみよう．Crystal の用語辞典より引用する．

subject (n.) (S, sub, SUB, Subj, SUBJ) A term used in the analysis of GRAMMATICAL FUNCTIONS to refer to a major CONSTITUENT of SENTENCE or CLAUSE structure, traditionally associated with the 'doer' of an action, as in The cat bit the dog. The oldest approaches make a twofold distinction in sentence analysis between subject and PREDICATE, and this is still common, though not always in this terminology; other approaches distinguish subject from a series of other elements of STRUCTURE (OBJECT, COMPLEMENT, VERB, ADVERBIAL, in particular. Linguistic analyses have emphasized the complexity involved in this notion, distinguishing, for example, the grammatical subject from the UNDERLYING or logical subject of a sentence, as in The cat was chased by the dog, where The cat is the grammatical and the dog the logical subject. Not all subjects, moreover, can be analyzed as doers of an action, as in such sentences as Dirt attracts flies and The books sold well. The definition of subjects in terms of SURFACE grammatical features (using WORD-ORDER or INFLECTIONAL criteria) is usually relatively straightforward, but the specification of their function is more complex, and has attracted much discussion (e.g. in RELATIONAL GRAMMAR). In GENERATIVE grammar, subject is sometimes defined at the NP immediately DOMINATED by S. While NP is the typical formal realization of subject, other categories can have this function, e.g. clause (S-bar), as in That oil floats on water is a fact, and PP as in Between 6 and 9 will suit me. The term is also encountered in such contexts as RAISING and the SPECIFIED-SUBJECTION CONDITION.

　昨日引用・参照した McArthur の記述と重なっている部分もあるが，今回の Crystal の記述からは，拠って立つ言語理論に応じて主語の捉え方が異なることがよく分かる．関係文法では主語の果たす機能に着目しており，生成文法ではそもそも主語という用語を常用しない．あらためて主語とは伝統文法に基づく緩い用語であり，そしてその緩さ加減が適切だからこそ広く用いられているのだということが分かる．

　・ Crystal, David, ed. A Dictionary of Linguistics and Phonetics. 6th ed. Malden, MA: Blackwell, 2008. 295--96.

[ 固定リンク | 印刷用ページ ]

■ #5457. 主語をめぐる論点 [subject][terminology][semantics][syntax][logic][existential_sentence][construction][agreement][number][expletive]

　昨日の記事「#5456. 主語とは何か？」 ([2024-04-04-1]) に引き続き，主語 (subject) についての本質的な疑問に迫りたい．この問題を論じるに際し，まず用語辞典などに当たってみるのが良さそうだ．McArthur の項目を引用しよう．主要な論点が見えてくる．

SUBJECT [13c: from Latin subjectum grammatical subject, from subiectus placed close, ranged under]. A traditional term for a major constituent of the sentence. In a binary analysis derived from logic, the sentence is divided into subject and predicate, as in Alan (subject) has married Nita (predicate). In declarative sentences, the subject typically precedes the verb: Alan (subject) has married (verb) Nita (direct object). In interrogative sentences, it typically follows the first or only part of the verb: Did (verb) Alan (subject) marry (verb) Nita (direct object)? The subject can generally be elicited in response to a question that puts who or what before the verb: Who has married Nita?---Alan. Where concord is relevant, the subject determines the number and person of the verb: The student is complaining/The students are complaining; I am tired/He is tired. Many languages have special case forms for words in the subject, the subject requires a particular form (the subjective) in certain pronouns: I (subject) like her, and she (subject) likes me.

Kinds of subject. A distinction is sometimes made between the grammatical subject (as characterized above), the psychological subject, and the logical subject: (1) The psychological subject is the theme or topic of the sentence, what the sentence is about, and the predicate is what is said about the topic. The grammatical and psychological subjects typically coincide, though the identification of the sentence topic is not always clear: Labour and Conservative MPs clashed angrily yesterday over the poll tax. Is the topic of the sentence the MPs or the poll tax? (2) The logical subject refers to the agent of the action; our children is the logical subject in both these sentences, although it is the grammatical subject in only the first: Our children planted the oak sapling; The oak sapling was planted by our children. Many sentences, however, have no agent: Stanley has back trouble; Sheila is a conscientious student; Jenny likes jazz; There's no alternative; It's raining

Pseudo-subjects. The last sentence also illustrates the absence of a psychological subject, since it is obviously not the topic of the sentence. This so-called 'prop it' is a dummy subject, serving merely to fill a structural need in English for a subject in a sentence. In this respect, English contrasts with languages such as Latin, which can omit the subject, as in Veni, vidi, vici (I came, I saw, I conquered: with no need for the Latin pronoun ego, I). Like prop it, 'existential there' in There's no alternative is the grammatical subject of the sentence, but introduces neither the topic nor (since there is no action) the agent.

Non-typical subjects. Subjects are typically noun phrases, but they may also be finite and non-finite clauses: 'That nobody understands me is obvious'; 'To accuse them of negligence was a serious mistake'; 'Looking after the garden takes me several hours a week in the summer.' In such instances, finite and infinitive clauses are commonly post and anticipatory it takes their place in subject position: 'It is obvious that nobody understands me'; 'It was a serious mistake to accuse them of negligence.' Occasionally, prepositional phrases and adverbs function as subjects: 'After lunch is best for me'; 'Gently does it.'

Subjectless sentences. Subjects are usually omitted in imperatives, as in Come here rather than You come here. They are often absent from non-finite clauses ('Identifying the rioters may take us some time') and from verbless clauses ('New filters will be sent to you when available'), and may be omitted in certain contexts, especially in informal notes (Hope to see you soon) and in coordination (The telescope is 43 ft long, weighs almost 11 tonnes, and is more than six years late).

　項目の書き出しは標準的といってよく，おおよそ文法的な観点から主語の概念が導入されている．主部・述部の区別に始まり，主語の統語論的振る舞いや形態論的性質が紹介される．
　次の節では，主語が文法的な観点のみならず心理的，論理的な観点からもとらえられるとして，別のアングルが提供される．心理的な観点からは「テーマ，主題」，論理的な観点からは「動作の行為者」に対応するのが主語なのだと説かれる．現実の文に当てはめてみると，3つの観点からの主語が必ずしも互いに一致しないことが示される．
　続けて，擬似的な主語，いわゆる形式主語やダミーの主語と呼ばれるものが紹介される．そこでは there is の存在文 (existential_sentence) も言及される．この構文では there はテーマではありえないし，動作の行為者でもないので，あくまで文法形式のために要求されている主語とみなすほかない．
　通常，主語は名詞句だが，それ以外の統語カテゴリーも主語として立ちうるという話題が導入されたあと，最後に主語がない（あるいは省略されている）節の例が示される．
　ほかにも様々に論点は挙げられそうだが，今回は手始めにここまで．

　・ McArthur, Tom, ed. The Oxford Companion to the English Language. Oxford: OUP, 1992.

[ 固定リンク | 印刷用ページ ]

■ #5456. 主語とは何か？ [subject][terminology][semantics][syntax][logic][existential_sentence][inohota][youtube][voicy][heldio][construction][agreement][number][link]

　3月31日に配信した YouTube 「いのほた言語学チャンネル」の第219回は，「古い文法・新しい文法　There is 構文まるわかり」と題してお話ししています．本チャンネルとしては，この4日間で視聴回数3100回越えとなり，比較的多く視聴されているようです．ありがとうございます．
　There is a book on the desk. のような存在文 (existential_sentence) における there は，意味的には空疎ですが，文法的には主語であるかのような振る舞いを示します．一方，a book は何の役割をはたしているかと問われれば，これこそが主語であると論じることもできます．さらに be 動詞と数の一致を示す点でも，a book のほうが主語らしいのではないかと議論できそうです．
　これまで当たり前のように受け入れてきた主語 (subject) とは，いったい何なのでしょうか．考え始めると頭がぐるぐるしてきます．存在文の主語の問題，および「主語」という用語に関しては，heldio でも取り上げてきました．

　・ 「#1003. There is an apple on the table. --- 主語はどれ？」
　・ 「#1032. なぜ subject が「主語」？ --- 「ゆる言語学ラジオ」からのインスピレーション」

　もちろんこの hellog でも，存在文に関連する話題は以下の記事で取り上げてきました．

　・ 「#1565. existential there の起源 (1)」 ([2013-08-09-1])
　・ 「#1566. existential there の起源 (2)」 ([2013-08-10-1])
　・ 「#4473. 存在文における形式上の主語と意味上の主語」 ([2021-07-26-1])

　主語とは何か？　簡単に解決する問題ではありませんが，ぜひ皆さんにも考えていただければ．

[ 固定リンク | 印刷用ページ ]

■ #5439. 英語辞書から集めた tautology （類語反復，トートロジー）の事例 [tautology][voicy][heldio][rhetoric][logic][pragmatics][semantics][khelf][aokikun][word_play][periphrasis]

　今朝の Voicy 「英語の語源が身につくラジオ (heldio)」の配信回は「#1022. トートロジー --- khelf 会長，青木くんの研究テーマ」です．言語における tautology とは何か？　"A is A" のような一見無意味な形式がなぜ存在し，なぜしばしば有意味となり得るのか？　この問題については，khelf（慶應英語史フォーラム）会長の青木輝さんとともに今後ゆっくりと検討していく予定ですが，今回はその頭出しという趣旨での配信でした．ぜひお聴きいただければ．
　トートロジーについては，hellog では「#4851. tautology」 ([2022-08-08-1]) としてすでに導入しています．今回は英語辞書から英語のトートロジーの事例をいくつか集めてみました．

　・ a beginner who has just started
　・ free gift
　・ He lives alone by himself.
　・ hear with one's ears
　・ helpful assistance
　・ necessary essentials
　・ new innovation
　・ real truth
　・ She is dumb and can not speak.
　・ speak all at once together
　・ the modern university of today
　・ The money should be adequate enough.
　・ They spoke in turn, one after the other.
　・ This candidate will win or not win.
　・ very excellent
　・ widow woman

　論理，意味，語用，形式などの観点から様々に分類できそうです．ものによっては periphrasis （迂言法），pleonasm （冗語法），redundancy （冗長），repetition （繰り返し）などと呼び変えるほうが適切な事例もありそうです．また，言葉遊び (word_play) とも関係してきそうです．
　言語によってトートロジーの種類は異なるのか？　個別言語におけるトートロジーの起源と発達は？　トートロジーの言語的機能は？　謎が謎を呼ぶ，深掘りしがいのあるテーマです．

[ 固定リンク | 印刷用ページ ]

■ #5174. 不定代名詞・決定詞 [pronoun][personal_pronoun][generic][indefinite_pronoun][determiner][assertion][semantics][logic]

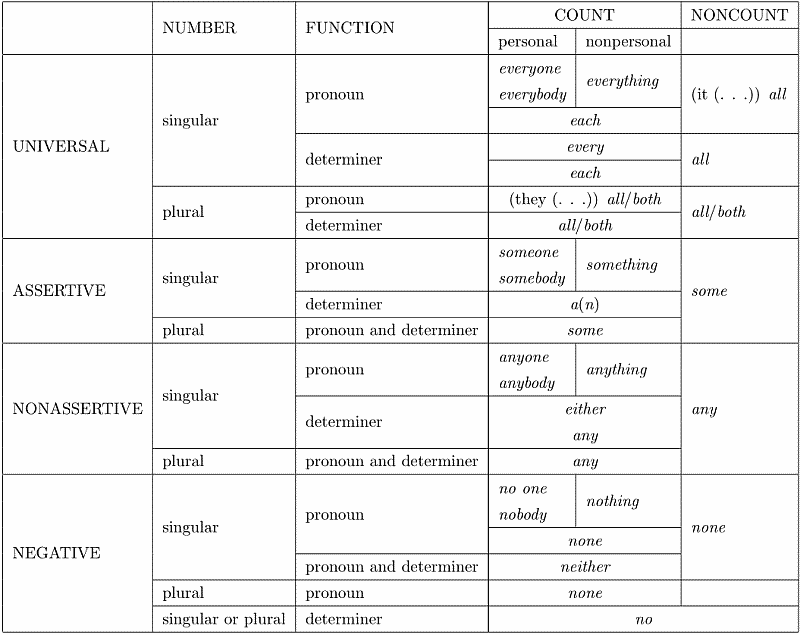
　現代英語には不定代名詞 (indefinite_pronoun) や不定決定詞 (indefinite determiner) という語類の体系がある．不定 (indefinite) の反対は定 (definite) である．例えば人称代名詞，再帰代名詞，所有代名詞，指示代名詞，そしてときに疑問代名詞にも定的な要素が確認されるが，不定代名詞にはそれがみられない．ただし，不定代名詞・決定詞は，むしろ論理的観点から，量的である (quantitative) ととらえてもよいかもしれない．全称的 (universal) か部分的 (partitive) かという観点である．
　Quirk et al. (§6.45) に主要な不定代名詞・決定詞の一覧表がある．こちらを掲載しよう．体系的ではあるが，なかなか複雑な語類であることがわかるだろう．

　・ Quirk, Randolph, Sidney Greenbaum, Geoffrey Leech, and Jan Svartvik. A Comprehensive Grammar of the English Language. London: Longman, 1985.

[ 固定リンク | 印刷用ページ ]

■ #4851. tautology [tautology][rhetoric][logic][semantics][pragmatics][construction_grammar]

　tautology （類語反復，トートロジー）は，まずもって修辞学 (rhetoric) の用語として発展してきた．ギリシア語の tautó (the same) + lógos (word) に起源をもち，ラテン語を経て，16世紀半ばに英語に借用された．以下『新英語学辞典』の tautology の項目に従って概説を与える．
　修辞学では冗語法 (pleonasm) や重言と同義に用いられる (cf. 「#2191. レトリックのまとめ」 ([2015-04-27-1]))．例えば a philatelist who collects stamps, These words come out successively one after another., Will you repeat that again? の類いの表現だ．「#3907. 英語の重言」 ([2020-01-07-1]) に類例がたくさん挙げられているが，それほど日常的で慣用的な語法ということでもある．
　tautology の構文の典型は "A is A." という形式である．意味論にいえば，主語概念のなかにすでに述語概念が含まれてしまっているために，新情報が付されないことになり，その限りにおいて文は「無意味」となる．別の角度からいえば，この構文は意味論的に常に真となる．"A is A." のほかに Philatelists collect stamps., The man who won won., Lynda loves the boy she loves. のような構文もある．これらは分析文 (analytic sentence) と呼ばれることがある．
　tautology は意味論的にいえば上記の通り「無意味」だが，語用論的には必ずしも無意味ではなく，むしろ豊かな含意が生み出されるといわれる．Philatelists collect stamps. の場合，philatelist （切手収集家）は比較的難しい単語であり，その単語の意味を説明するために，この文が発せられている可能性がある．また，The man who won won. については，相手をはぐらかす意図で発せられているのかもしれない．
　語用論では，tautology は Grice の協調の原理 (cooperative_principle) のもとで論じられることが多い．tautology の発話者が協調の原理をあえて違反しようとしているわけではないと判断されるのであれば，聞き手はその tautology に隠された意味や意図を見出そうとするだろう．こうして何らかの含意が生み出されるのである．
　tautology は意味論的には無意味であっても語用論的にはしばしば有意味となる．この不思議さこそが，tautology が語用論や認知言語学で注目される所以だろう．
　関連して「#1122. 協調の原理」 ([2012-05-23-1])，「#1133. 協調の原理の合理性」 ([2012-06-03-1])，「#1134. 協調の原理が破られるとき」 ([2012-06-04-1]) を参照．

　・ 大塚 高信，中島 文雄（監修）　『新英語学辞典』　研究社，1982年．

[ 固定リンク | 印刷用ページ ]

■ #4654. either は片方なのか両方なのか問題 [sobokunagimon][pronoun][adjective][dual][logic][semantics][contronym][khelf]

　一昨日の記事「#4652. any が「どんな?でも」を表わせるように either は「いずれの?でも」を表わせる」 ([2022-01-21-1]) でもすでに取り上げましたが，標記は目下私のゼミを中心とする khelf (= Keio History of the English Language Forum) メンバーの間で熱い議論の対象となっている問題です．
　either は，2者のうちのいずれかを選ぶ「片方」の意味を表わすというイメージが強いと思いますが，実は「両方」の意味を表わすケースもあるという問題です．一種の contronym の例といえます．
　『コンパスローズ英和辞典』の either より，それぞれに対応する語義1と語義2を引用しましょう．

--- （形）［単数形の名詞につけて］
(1) （2つ［2人］のうち）どちらか（一方）の；どちらの…でも，どちらでも任意の
   Take either apple.｜どちらかのりんごを取りなさい
   You may invite either boy.｜どちらの少年を招待しても結構です．
. . . .
(3) どちらの…も，両方の
   There was a chair at either end of the long table.｜長いテーブルの両端にそれぞれいすが置かれていた．

（語法）3の意味では特に side, end, hand など対を表わす名詞と用いるが， 次の例のように both（＋複数名詞）や each（＋単数名詞）を用いることも多い．both は「両方」を同時にまとめて，either, each は「片方」 ずつそれぞれを個別に捉える感じとなる
   There were chairs at both ends of the long table.
   There was a chair at each end of the long table.

　either A or B という高頻度の相関表現がありますし，一般には (1) こそが either の原義だと捉えられていると思いますが，歴史的にみれば驚くことに (3) のほうが古いのです．OED によれば，(3) は古英語から普通に見られる語義ですが，(1) は中英語後期になってようやく現われる新参語義です．
　どうしてこんなことになってしまったのでしょうか．よく似た形態の outher という語とややこしい関係に陥ってしまったという事情があるようです．関連して「#945. either の2つの発音」 ([2011-11-28-1]) もご参照ください．

[ 固定リンク | 印刷用ページ ]

■ #4652. any が「どんな?でも」を表わせるように either は「いずれの?でも」を表わせる [pronoun][adjective][assertion][dual][logic][semantics][contronym]

　Any child can do that. という文は「どんな子供でもそれができる」の意を表わします．力点の置き方は異なりますが，基本的な意味としては All children can do that. とおよそ同等です．
　平行的な例を挙げます．Either way will do. という文は「いずれのやり方でもうまく行きます」の意を表わします．力点の置き方は異なりますが，基本的な意味としては Both ways will do . とおよそ同等です．
　特に2つめの either と both を用いた例文ペアが同義で用いられ得るというのは，なかなかの驚きではないでしょうか．というのは，私たちは either (A or B) と both (A and B) は対義表現であると信じ込まされてきたからです．しかし，この2つは文脈によってはむしろ類義表現というべきものになり得るのです．
　either は，一般には2つあるものの「いずれか」「片一方」を意味すると理解されていますが，実は「いずれの○○でも（よい）」という関連する語義からは「○○の両方であっても（よい）」の解釈が生じ得ます．論理学の喩えでいえば，or には「排他的選言」 (exclusive disjunction) と「非排他的選言」 (inclusive disjunction) の両義があることに相当するでしょうか．
　ということで，多少のニュアンスの違いはありながらも，either は both でパラフレーズできてしまうケースがあるのです．例えば，次の例を参照．

　・ Unfortunately I was sitting at the table with smokers on either side of me.
　・ Unfortunately I was sitting at the table with smokers on both sides of me.

　この either vs both の意味論的緊張関係は，any vs all の緊張関係とパラレルです．前者は2つのものについて，後者は3つ以上のものについて，という違いがあるだけです (cf. Quirk et al. §6.61）．言い換えれば，前者は意味論的に両数あるいは双数 (dual) の性質をもっているということです．
　印欧語の数カテゴリーの重要なメンバーだった両数は，英語にも化石的な形ではありますが，所々に痕跡を残しています．both, either, neither, other, whether など -er をもつものが多いですね (cf. 「#3005. or の語源」 ([2017-07-19-1])) ．

　・ Quirk, Randolph, Sidney Greenbaum, Geoffrey Leech, and Jan Svartvik. A Comprehensive Grammar of the English Language. London: Longman, 1985.

[ 固定リンク | 印刷用ページ ]

■ #4428. hedge と prototype の関係 [hedge][prototype][semantics][pragmatics][logic]

　連日「#4426. hedge」 ([2021-06-09-1]) と「#4427. 様々な hedge および関連表現」 ([2021-06-10-1]) のように hedge の話題を取り上げている．今回も Lakoff の論文を参照して考察を続けたい．
　論文を読んで hedge の理解が変わってきた．昨日の記事の最後でも述べたが，単なる「ぼかし言葉」ではなく「ある命題を真たらしめる条件を緩く指定・制限する方略」と理解すべきだろう．少なくとも Lakoff の考える hedge はそのようなものらしい．そうすると，議論は必然的に意味論から語用論の方面に広がっていくことになるだろうし，意味に関する検証主義という言語哲学の問題にもつながっていきそうだ．
　hedge と prototype の深い関係も明らかになった．例えば，sort of という hedge は，プロトタイプから少々逸脱したものを許容する方向に作用する意味論・語用論上の「関数」とみることができる．実際，Lakoff はファジー集合を提唱した Lofti Zadeh の研究よりインスピレーションを受け，論理学・代数学的な関数を利用して tall, very tall, sort of tall, pretty tall, rather tall の意味分析を行なっている．Lakoff 論文 (482) より，以下の図を見てもらいたい．



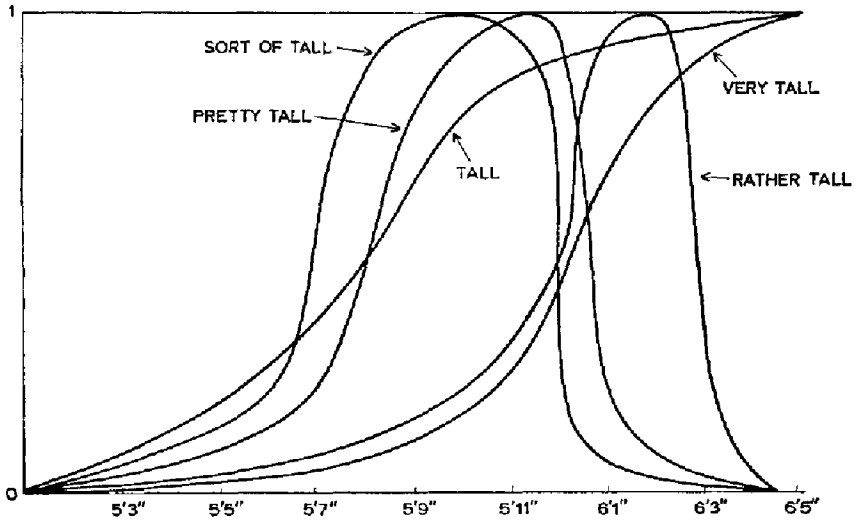
　この図の見方は次の通りだ．「ある人が tall, very tall, sort of tall, pretty tall, rather tall である」という命題がある場合，実際にどれくらいの背の高さであれば，その命題は真であると考えられるかについて多数の人にアンケートを取った結果のサマリーと読める．つまり，5'3" （5フィート3インチ≒160cm）で tall とみなす回答者はほぼ0%だろうが，6'3" （6フィート3インチ≒190cm）であればほぼ100%の回答者が tall を妥当な形容詞とみなすだろう．6'3" であれば，very tall ですら100%に近い高い値を示すだろう．しかし，rather tall は 6'3" に対しては，大方かえって不適切な表現と判断されるだろう，等々．
　要するに，5種類の表現に対して描かれた各曲線の形状が，その表現の hedge としての効果である，と解釈できる．これらは曲線であるから，代数的には関数として表現できることになる．もちろん Lakoff とて何らかの定数を与えた厳密な意味での関数の立式を目指しているわけではないのだが，hedge と prototype の関係がよく分かる考え方ではある．
　この点について Lakoff 自身の要約 (492--93) を引用しておこう．

6.5. Algebraic Functions Play a Role in the Semantics of Certain Hedges

Hedges like SORT OF, RATHER, PRETTY, and VERY change distribution curves in a regular way. Zadeh has proposed that such changes can be described by simple combinations of a small number of algebraic functions. Whether or not Zadeh's proposals are correct in all detail, it seems like something of the sort is necessary. . . .

6.6. Perceptual Finiteness Depends on an Underlying Continuum of Values

Since people can perceive, for each category, only a finite number of gradations in any given context, one might be tempted to suggest that fuzzy logic be limited to a relatively small finite number of values. But the study of hedges like SORT OF, VERY, PRETTY, and RATHER, whose effect seems to be characterizable at least in part by algebraic functions, indicates that the number and distribution of perceived values is a surface matter, determined by the shape of underlying continuous functions. For this reason, it seems best not to restrict fuzzy logic to any fixed finite number of values. Instead, it seems preferable to attempt to account for the perceptual phenomena by trying to figure out how, in a perceptual model, the shape of underlying continuous functions determines the number and distribution of perceived values.

　いつの間にかファジー集合という抜き差しならない領域にまで到達してしまったが，そもそも hedge ＝「ぼかし（言葉）」という認識から始まったわけなので，遠く離れていないようにも思えてきた．

　・ Lakoff, G. "Hedges: A Study in Meaning Criteria and the Logic of Fuzzy Concepts." Journal of Philosophical Logic 2 (1973): 458--508.

[ 固定リンク | 印刷用ページ ]