hellog〜英語史ブログ / 2009-08-08

■ #103. グリムの法則とは何か [consonant][grimms_law]

　昨日の記事[2009-08-07-1]で，hundred を例としてグリムの法則 ( Grimm's Law ) を簡単に説明した．今後もいろいろと話題にすることがあると思うので，今回はもう少し丁寧に解説を．
　グリムの法則はヴェルネルの法則 ( Verner's Law ) とあわせて，第一次ゲルマン子音推移 ( First Germanic Consonant Shift ) と呼ばれ，紀元前1000?400年あたりにゲルマン語派が経た一連の音声変化を定式化したものである．「法則」というくらいだから，例外なき完璧な適用性を売りにしており，確かにその信頼性は高い．一見するとグリムの法則の例外に思えるものも，ヴェルネルの法則によって改めて説明することができるなど，二つの法則を合わせると，まさに「音韻法則に例外なし」と謳いたくなるような芸術的完璧さである．昨日[2009-08-07-1]の hund(red) -- centum の例では，Indo-European */k/ > Germanic */h/ の子音変化が起こったことを確認したが，これはグリムの法則を構成する一連の変化の一例に過ぎない．
　グリムの法則の示す子音変化は，印欧祖語の「閉鎖音」の系列に生じた．閉鎖音は破裂音とも呼ばれ，口の中のどこかで呼気を一度せきとめ，それを勢いよく開け放つ（破裂させる）ときに発せられる子音である（[2009-05-29-1]の子音表を参照）．印欧祖語では，閉鎖音系列は次のような体系をなしていた．



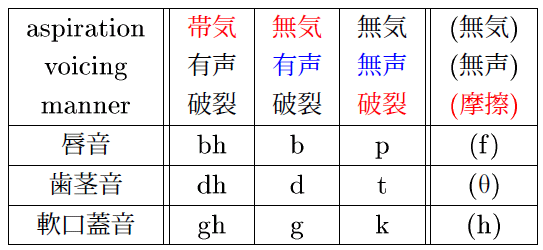
　印欧祖語では，最右列の3音を除き，全部で9音の閉鎖音があった．隣り合う列どうしは，調音様式が互いに少しだけ異なっているだけで，調音音声学的には非常に近い関係にある．例えば左上の bh は，「帯気」を「無気」に変化させる（呼気を弱める）ことによって簡単に b になる．そして，その b は，「有声」を「無声」にすれば（清音にすれば）すぐに p になる．さらに，その p は「破裂」（「閉鎖」に同じ）を弱めて「摩擦」化すれば f となる，等々．
　子音組織はこのように体系的であるから，それが変化するときにも体系的な変化の仕方を示す．次の図は，グリムの法則を経た後のゲルマン祖語の閉鎖音系列である．



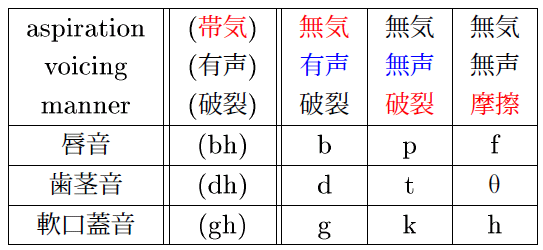
　印欧祖語の閉鎖音の表とほぼ同じだが，ゲルマン祖語の閉鎖音系列は，最左列の3音を除いた9音で構成されていた．二つの表を見比べればわかるとおり，グリムの法則とは，各列の音がすぐ右の列の音へ規則正しく変化した過程に他ならない．
　「変化の仕方が体系的だった」ことはこれで分かったと思うが，変化の順序はどうだったろうか．3列すべてがイッセーノーセッで右列に移行したわけではなく，右端から順番に起こったことが分かっている．すなわち，まず印欧祖語の右列 p t k が f θ h へ変化し，その次に中列の b d g が今や空席となった p t k のスロットを埋めた．そして最後に，左列の bh dh gh が今や空席となった b d g のスロットを埋めた．これを図示すると以下のようになる．

[ 固定リンク | 印刷用ページ ]