教師あり学習において，特に予測に重点が置かれる場合，手元のデータとモデルの適合ばかりを考えてしまうと，そのデータを説明するだけのモデルが出来上がってしまう．これでは，正解のない説明変数Xだけの将来のデータへ適合しない可能性がある．これは過剰適合(over-fitting)の問題としてよく知られている．
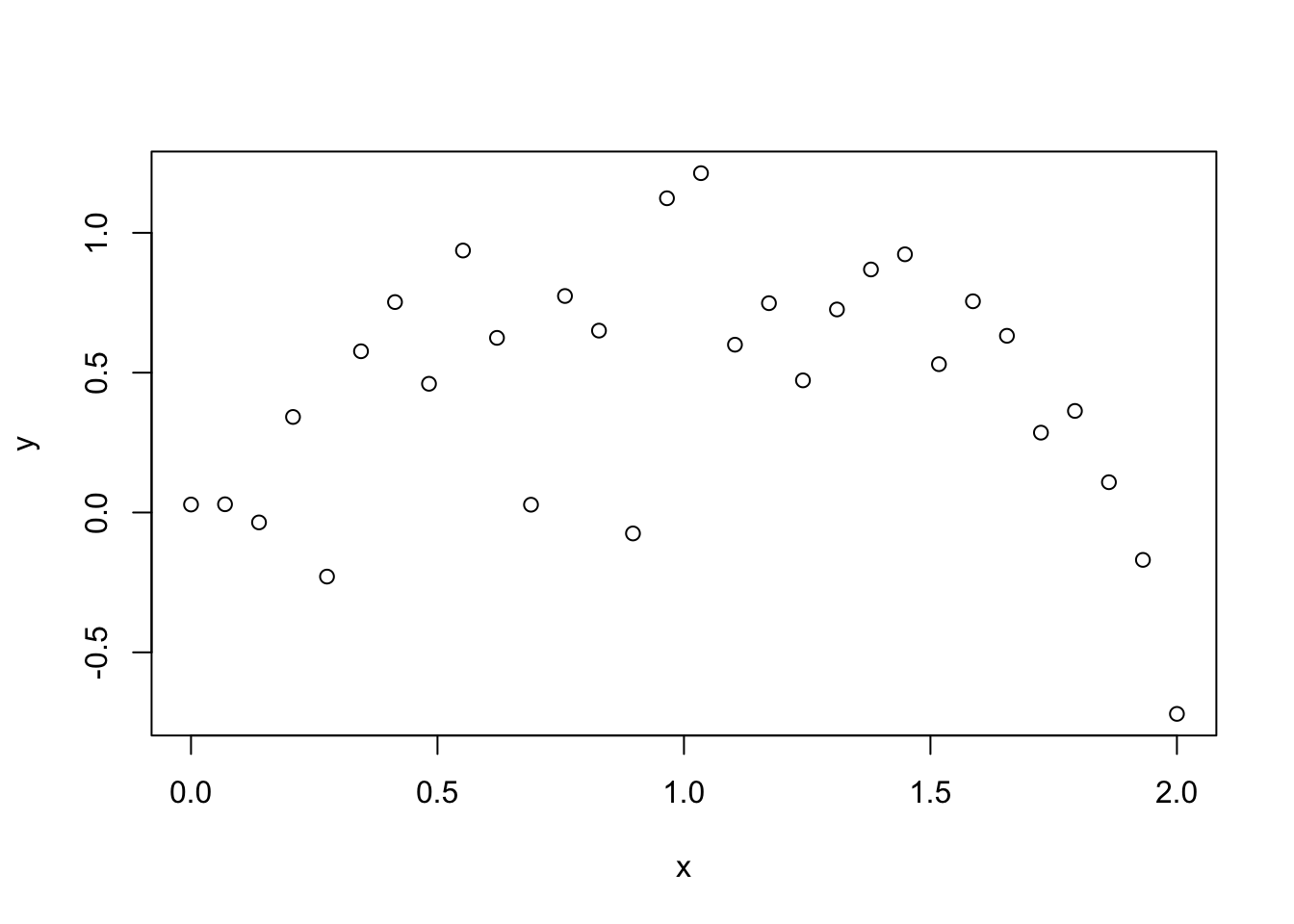
この過剰適合の問題を，多項式回帰を用いたトイデータで確認してみよう． いま，(Y,X)のデータが次のように得られたとしよう．もちろん，Yの生成過程は通常は未知であるが，今回は説明のために既知のトイデータを考える．
x <- seq(0,2,length=30)
y <- 0.5*x + 1.2*x^2 - 0.8*x^3 + rnorm(length(x),0,0.3)
toydata <- data.frame(x,y)
head(toydata) x y
1 0.00000000 0.02852667
2 0.06896552 0.02946404
3 0.13793103 -0.03542440
4 0.20689655 0.34162883
5 0.27586207 -0.22914801
6 0.34482759 0.57652809 plot(toydata$x, toydata$y, xlab="x", ylab="y")
このデータにK次の多項式回帰モデル，すなわち，
Y = \beta_{0} + \beta_{1}X + \beta_{2}X^{2} + \cdots + \beta_{K}X^{K} + \varepsilon
を適合させ，決定係数を確認してみる．
r1 <- summary(lm(y~x, data=toydata)) #1次
r3 <- summary(lm(y~x+I(x^2)+I(x^3),data=toydata)) #3次
r5 <- summary(lm(y~x+I(x^2)+I(x^3)+I(x^4)+I(x^5),data=toydata)) #5次
r7 <- summary(lm(y~x+I(x^2)+I(x^3)+I(x^4)+I(x^5)+I(x^6)+I(x^7),data=toydata)) #7次
r9 <- summary(lm(y~x+I(x^2)+I(x^3)+I(x^4)+I(x^5)+I(x^6)+I(x^7)+I(x^8)+I(x^9),data=toydata)) #9次 rsquared <- data.frame(
K = c(1,3,5,7,9),
R2 = c(r1$r.squared,r3$r.squared,r5$r.squared,r7$r.squared,r9$r.squared) #決定係数のみをsummaryから取り出す
)
rsquared K R2
1 1 1.069275e-05
2 3 5.637970e-01
3 5 6.101251e-01
4 7 6.302649e-01
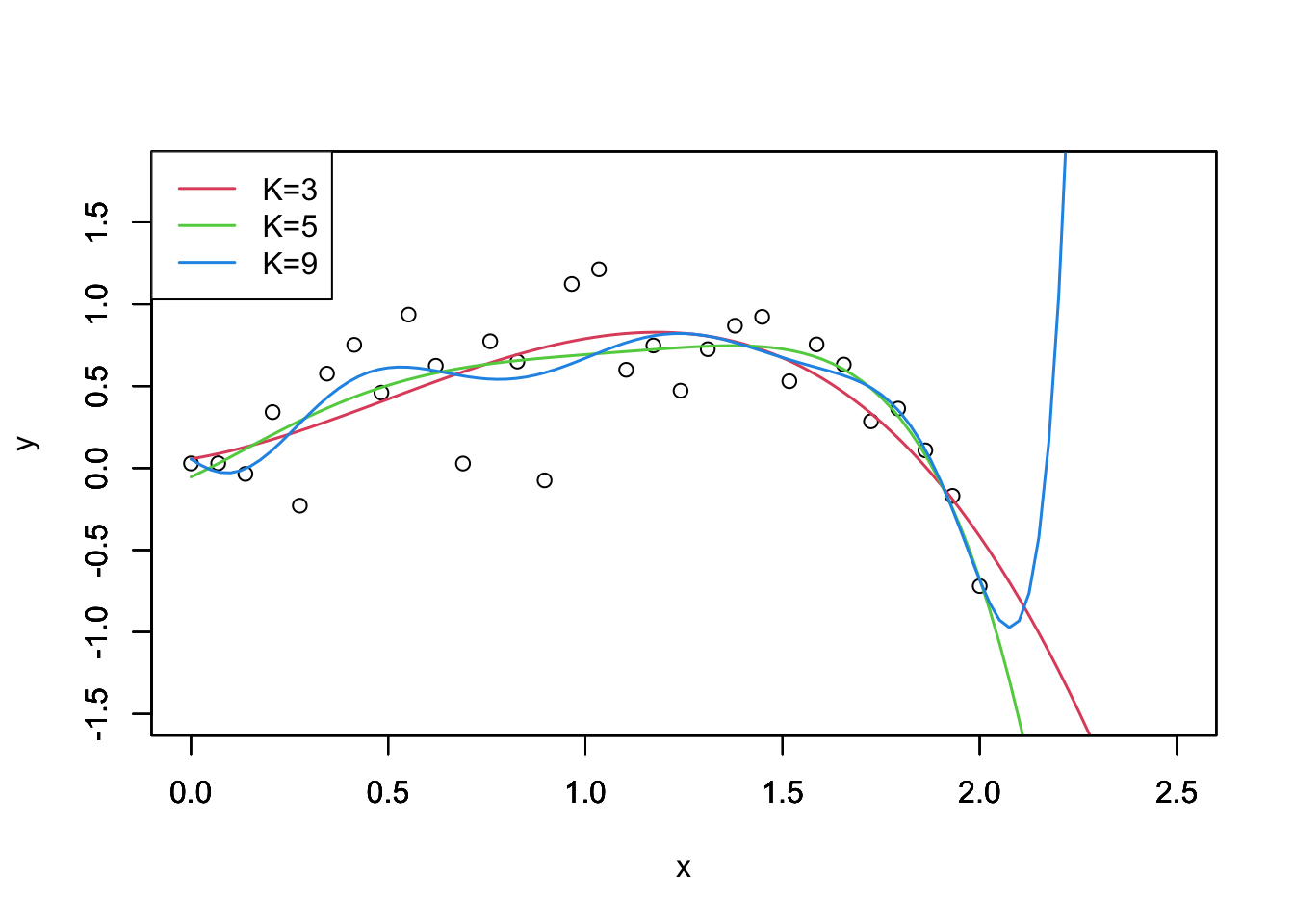
5 9 6.347331e-01次数Kを大きくすればするほど決定係数も1に近くなることが確認される．ではKを大きくすればするほど良いのだろうか． いくつかの次数に対するプロットを見てみよう．
f3 <- lm(y~x+I(x^2)+I(x^3),data=toydata)
f5 <- lm(y~x+I(x^2)+I(x^3)+I(x^4)+I(x^5),data=toydata)
f9 <- lm(y~x+I(x^2)+I(x^3)+I(x^4)+I(x^5)+I(x^6)+I(x^7)+I(x^8)+I(x^9),data=toydata)
cf3 <- coef(f3); cf5 <- coef(f5); cf9 <- coef(f9)
xlim <- c(0,2.5); ylim <- c(-1.5,1.8)
plot(x,y,xlim=xlim,ylim=ylim)
par(new=T)
curve(cf3[1] + cf3[2]*x + cf3[3]*x^2 + cf3[4]*x^3,xlim=xlim,ylim=ylim,xlab="",ylab="",col=2,lwd=1.5)
par(new=T)
curve(cf5[1] + cf5[2]*x + cf5[3]*x^2 + cf5[4]*x^3 + cf5[5]*x^4 + cf5[6]*x^5,xlim=xlim,ylim=ylim,xlab="",ylab="",col=3,lwd=1.5)
par(new=T)
curve(cf9[1] + cf9[2]*x + cf9[3]*x^2 + cf9[4]*x^3 + cf9[5]*x^4 + cf9[6]*x^5 + cf9[7]*x^6 +cf9[8]*x^7 + cf9[9]*x^8 + cf9[10]*x^9,xlim=xlim,ylim=ylim,xlab="",ylab="",col=4,lwd=1.5)
legend("topleft",legend=c("K=3","K=5","K=9"),lty=1,col=c(2,3,4),lwd=1.5,)
次数が大きくなるほど，観測値に過剰に適合してしまっていることが確認できる．特にK=9の場合，x>2においておかしな挙動を示している．トイデータの生成過程をみると，正解はK=3である．
では，どうやってモデルの性能評価を行えば良いのだろうか．ひとつの方法は，手元のデータ(説明変数と結果変数が揃っている)をトレーニング(訓練)データとテスト(検証)データに分割することである．このとき，分割は互いに共通部分が無いように行わなければならない．
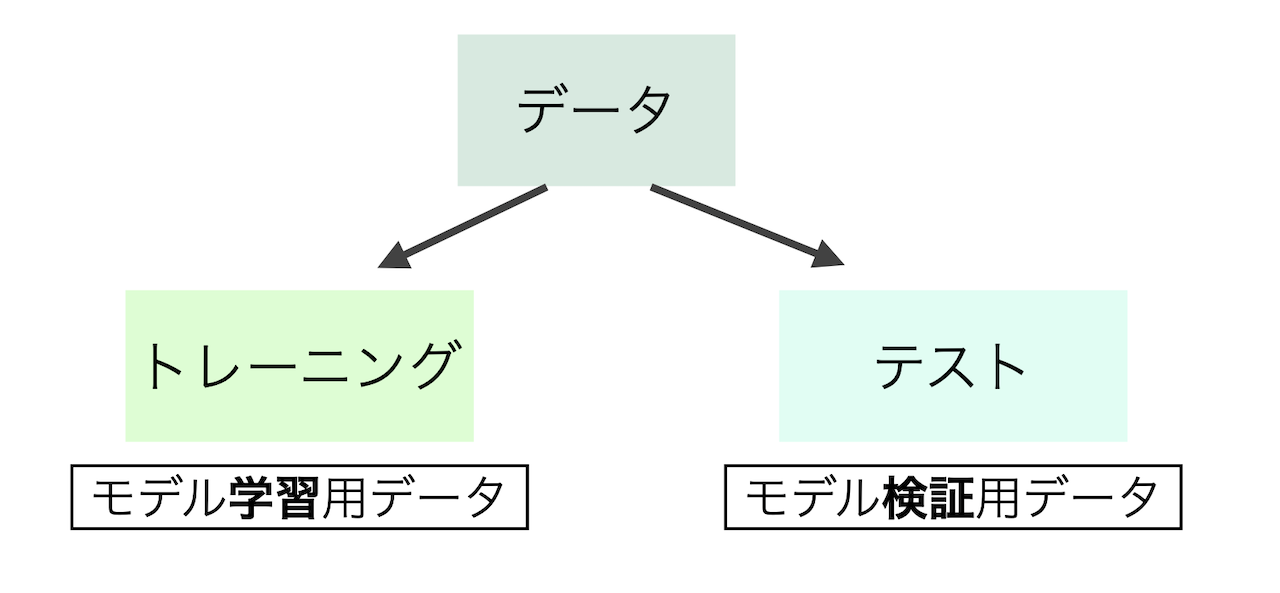
トレーニングデータを使って複数のモデル，例えば次数の異なる多項式回帰モデルや，Nearest Neighbor，ランダムフォレストなどを学習し，その性能をテストデータで評価する．
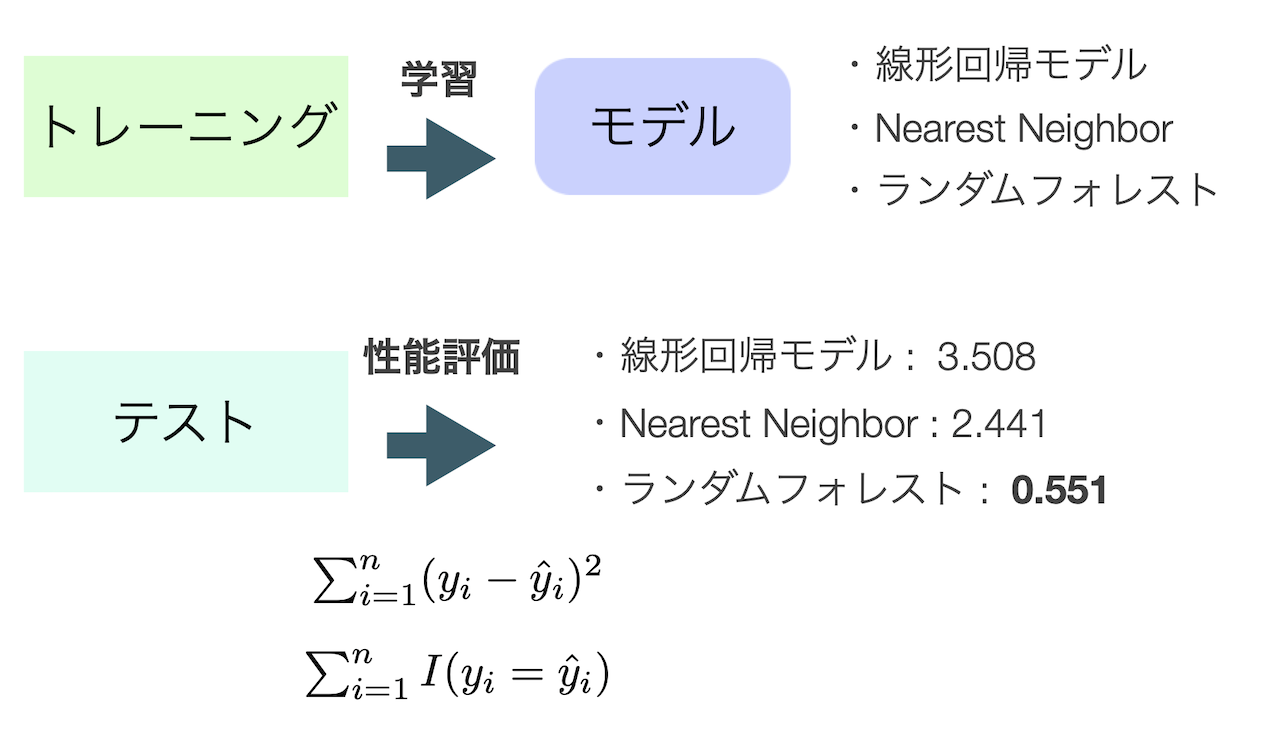
ただし，テストデータでの性能を見た後に，トレーニングデータでの学習を再度行ってはいけない． これでは分割した意味がなくなり，結局手元のデータに適合するようにモデルを学習してしまっている． テストデータは最終的なモデルの評価を行う時だけしか使ってはいけない．
実際にBostonデータを使って線形回帰モデルの性能評価を行ってみよう．
library(MASS)
head(Boston) crim zn indus chas nox rm age dis rad tax ptratio black lstat
1 0.00632 18 2.31 0 0.538 6.575 65.2 4.0900 1 296 15.3 396.90 4.98
2 0.02731 0 7.07 0 0.469 6.421 78.9 4.9671 2 242 17.8 396.90 9.14
3 0.02729 0 7.07 0 0.469 7.185 61.1 4.9671 2 242 17.8 392.83 4.03
4 0.03237 0 2.18 0 0.458 6.998 45.8 6.0622 3 222 18.7 394.63 2.94
5 0.06905 0 2.18 0 0.458 7.147 54.2 6.0622 3 222 18.7 396.90 5.33
6 0.02985 0 2.18 0 0.458 6.430 58.7 6.0622 3 222 18.7 394.12 5.21
medv
1 24.0
2 21.6
3 34.7
4 33.4
5 36.2
6 28.7次の3つの線形回帰モデルの性能評価を行いたい．すなわちmedvを予測するための説明変数が異なるモデル群である．
\begin{align*} {\tt medv} &= \beta_{0} + \beta_{1}{\tt crim} + \varepsilon \\ {\tt medv} &= \beta_{0} + \beta_{1}{\tt rm} + \beta_{2}{\tt age} + \varepsilon \\ {\tt medv} &= \beta_{0} + \beta_{1}{\tt tax} + \beta_{2}{\tt lstat} + \varepsilon \end{align*}
性能評価にはテストデータ(y_{i}, x_{i}), i=1,2,\dots,n_{\tt test}予測誤差 \frac{1}{n_{\tt test}} \sum_{i=1}^{n_{\tt test}}(y_{i} - \hat{y}_{i})^{2} を用いる．ここで，予測値\hat{y}_{i}における回帰係数の推定にはトレーニングデータを用いていることに注意が必要である．
まずはデータをトレーニングとテストに分割する．
nt <- 100 ##テストデータのサンプルサイズ
test.boston <- Boston[1:nt,] ##最初のnt行をテストデータに
train.boston <- Boston[(nt+1):506,] ##残りをトレーニングデータ次にトレーニングデータで回帰係数を学習する．
lm1 <- lm(medv~crim,data=train.boston)
lm2 <- lm(medv~rm+age,data=train.boston)
lm3 <- lm(medv~tax+lstat,data=train.boston)最後にテストデータにおいて予測誤差を計算する．
sum((test.boston[,"medv"] - predict(lm1,test.boston))^2)/nt[1] 37.96788 sum((test.boston[,"medv"] - predict(lm2,test.boston))^2)/nt[1] 6.780685 sum((test.boston[,"medv"] - predict(lm3,test.boston))^2)/nt[1] 27.65504よって3つのモデルの中では，説明変数にrmとageを用いたものが予測誤差の意味で一番良いことがわかる．
株価予測のためのデータセット(yは対数収益率)に対して，何時点前までの対数収益率を用いれば良いのか， 上記のように検証せよ．
多くのモデルには調整(チューニング)が必要なパラメータを持っている．例えば，
などである．チューニングにはもちろんトレーニングデータのみで行うべきであるが， 過剰適合の問題が再び生じてしまう．そこで，トレーニングデータの中で擬似的にテストデータを作り出す 交差検証法(クロスバリデーション)が有用となる．
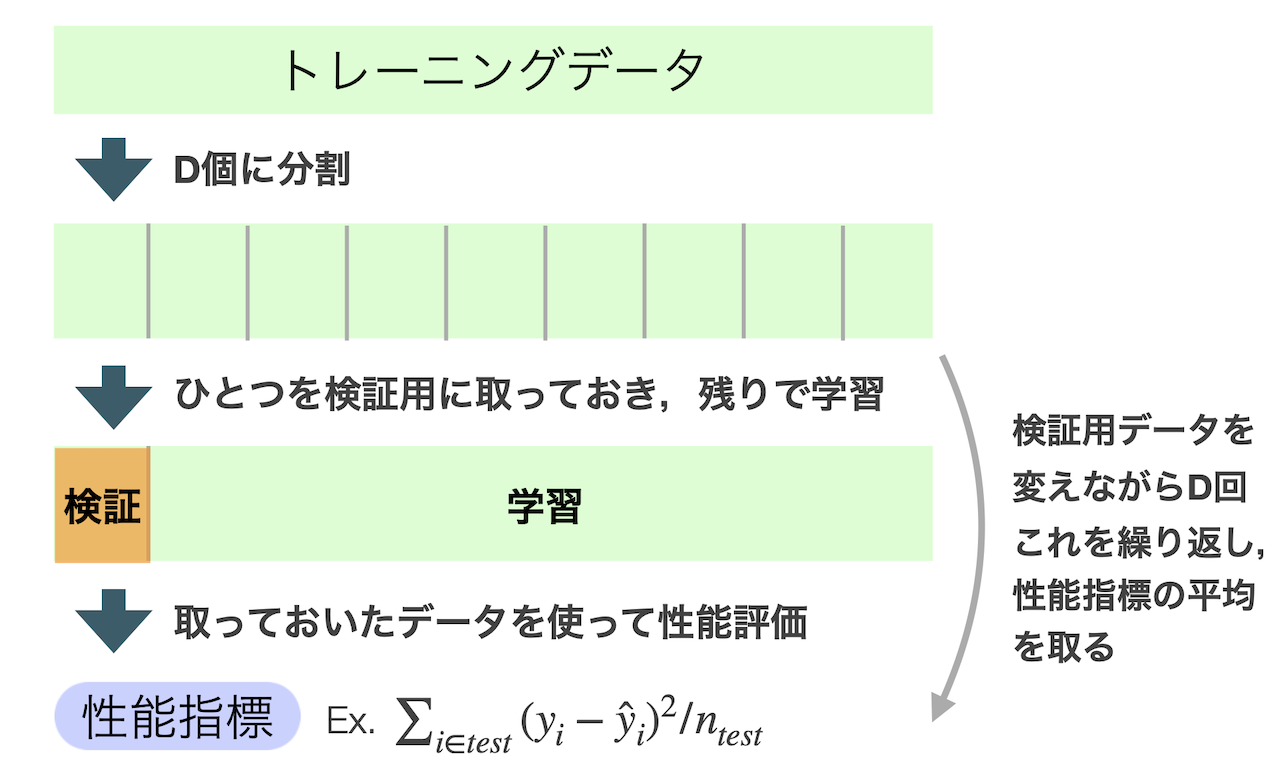
ここで，Dは分割数であり，経験的にD=5やD=10が良いとされる．Dをサンプルサイズで取るとき， すなわちひとつずつ検証用に取っていくとき，それを特にLeave-one-outクロスバリデーションと呼ぶ． これはトレーニングデータの個数が少ない時に有用である．
クロスバリデーションをAutoデータに対して実装してみよう．
library(ISLR)
head(Auto) mpg cylinders displacement horsepower weight acceleration year origin
1 18 8 307 130 3504 12.0 70 1
2 15 8 350 165 3693 11.5 70 1
3 18 8 318 150 3436 11.0 70 1
4 16 8 304 150 3433 12.0 70 1
5 17 8 302 140 3449 10.5 70 1
6 15 8 429 198 4341 10.0 70 1
name
1 chevrolet chevelle malibu
2 buick skylark 320
3 plymouth satellite
4 amc rebel sst
5 ford torino
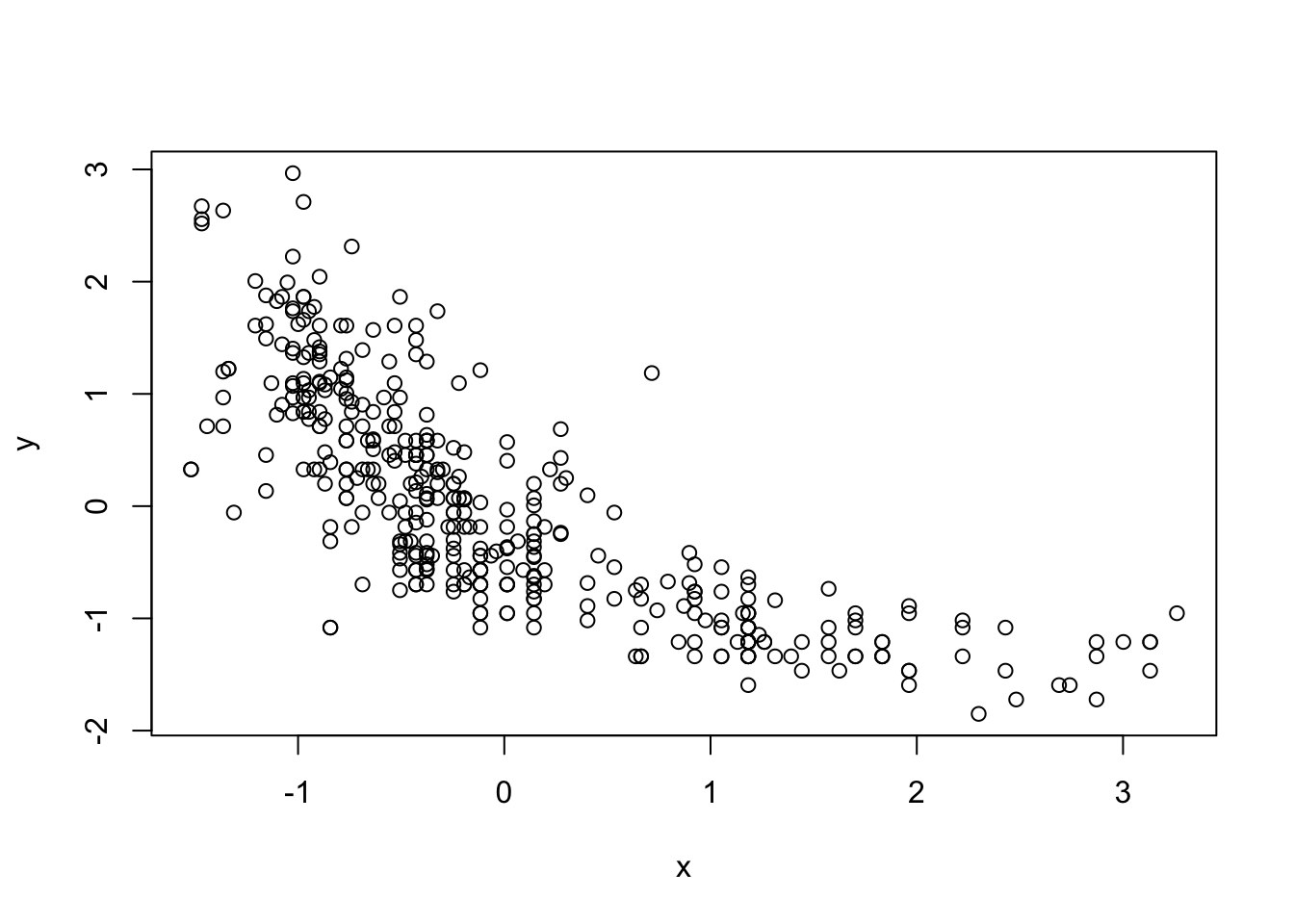
6 ford galaxie 500結果変数をmpg，説明変数をhorsepowerにした多項式回帰の次数Kをクロスバリデーションで選択する．
y <- scale(Auto$mpg) ##平均0分散1にスケーリングしておく
x <- scale(Auto$horsepower) ##yと同様にスケーリング
plot(x,y)
このときの具体的なクロスバリデーションの手順は下記のようになる．
これをR上で実装したのが以下のコードとなる．
X <- data.frame(y=y, x=x, x2=x^2, x3=x^3, x4=x^4, x5=x^5)
n <- dim(X)[1]
##n=392なので割り切れるD=8とする
fold.n <- n/8
error.out <- rep(0,5) ##Error_{K}用の箱
for(i in 1:5){
error.in <- rep(0,8) ##Error_{K,D}用の箱
data <- X[,1:(i+1)]
for(D in 0:7){
test.data <- data[(D*fold.n + 1):((D+1)*fold.n),]
train.data <- data[-( (D*fold.n + 1):((D+1)*fold.n) ),]
result <- lm(y~.,data=train.data)
yhat <- predict(result,test.data)
error.in[D+1] <- sum((test.data[,1] - yhat)^2)/fold.n
}
error.out[i] <- mean(error.in)
}
which.min(error.out)[1] 5上記のコードを修正してleave-on-outクロスバリデーションを実装せよ．