How to use R

1. 基本演算

電卓の代わりに使う

Rでは基本的な四則演算はもちろんのこと，べき乗や剰余の計算も簡単にできる．

1 + 1

[1] 2

5 - 3

[1] 2

2 * 5

[1] 10

10 / 2

[1] 5

4 ^ 10

[1] 1048576

10 %% 3

[1] 1

演算を組み合わせることもできる．コードを1行にまとめて書きたい場合は，記号;を使う．

  1 + (5-3) ^ 2;  (5 * 5 / 5) %% 3

[1] 5

[1] 2

簡単な関数

Rには平方根などの，簡単な関数も用意されている．以下に，よく利用しそうな関数を挙げておく．例えば，xの平方根は，sqrt(x)のように書く．記号#はコメントアウトの意味．#以下のコードは実行されない．

  sqrt(4) ## squared root

[1] 2

  abs(-5) ## absolute value

[1] 5

  exp(1) ## exponential, exp(x) or e^(x)

[1] 2.718282

  log(4);  log(4,10) ## 底がeの対数関数，底が10の対数関数

[1] 1.386294

[1] 0.60206

  sin(0.5); cos(0.5); tan(0.5) ## sin, cos, tan

[1] 0.4794255

[1] 0.8775826

[1] 0.5463025

  sign(5); sign(-5) ## sign function

[1] 1

[1] -1

数学関数には，log(x,10)のように，追加オプションを持つ場合がある．関数の詳細を知りたい場合は，Rからヘルプを呼び出せばよい．次のコードを実行してみよう．

  ?log

Exercise 1.1

関数roundをRのヘルプで調べ，数値12.345678を小数点第5位で四捨五入してみよう．

2. オブジェクト

Rでは，ある変数(オブジェクト)に数値・ベクトル・行列・文字列を代入することができる．代入には記号<-を用いる．記号=でもよい．

  x <- 4
  x

[1] 4

このコードは，xという変数に4を代入するという意味である．ちなみに，逆に書いてもよい．

  4 -> x

同じ変数に代入を繰り返し行うこともできるが，その場合は一番新しい値が代入されていることに注意しなければならない．

  x <- 4; x <- 8; x <- 100

すなわち，この場合はxに100という数値が代入されている．また，大文字と小文字はRでは区別される．

  x <- 100; X <- 10
  x; X

[1] 100

[1] 10

変数には，文字列を代入することもできる．その場合は代入したい文字列をダブルクオーテーションで囲む必要がある．

  v1 <- "weight"; v2 <- "height"; v3 <- "blood_type"

変数同士の演算も可能である．

  x1 <- 5
  x2 <- 10
  x1^2 - 3*x2 + sqrt(x2)

[1] -1.837722

Exercise 2.1

xとyに10と2をそれぞれ第入し，x^y, \sqrt{x}, e^{y}を計算せよ．

3. ベクトル

ベクトルの生成

記号cを使ってベクトルを記述することができる．例えば以下では，(1,2,3)というベクトルをxに代入している．

  x <- c(1,2,3)

ベクトル同士をつなげて，より大きなベクトルを作ることもできる．

  x <- c(1,2,3); y <- c(4,5,6)
  c(x,y); c(c(1,2,3),c(4,5,6))

[1] 1 2 3 4 5 6

[1] 1 2 3 4 5 6

ある規則性を持つベクトルは，簡単に作ることができる．その場合は記号:を用いる．

  1 : 10

 [1]  1  2  3  4  5  6  7  8  9 10

  10 : -3

 [1] 10  9  8  7  6  5  4  3  2  1  0 -1 -2 -3

  1 : 5 + 2

[1] 3 4 5 6 7

  1 : (5 + 2)

[1] 1 2 3 4 5 6 7

上記の3番目と4番目のコードでは結果が異なることに注意(何故違うのか考えよ)．より複雑なベクトルを作るためには，等差数列を返すseq関数や，同じ数値を一定個数並べるrep関数を使う．

  seq(1,10,by=1); seq(1,10,by=2); seq(1,10,by=3)

 [1]  1  2  3  4  5  6  7  8  9 10

[1] 1 3 5 7 9

[1]  1  4  7 10

  seq(0,1,length=10); seq(0,1,0.01)

 [1] 0.0000000 0.1111111 0.2222222 0.3333333 0.4444444 0.5555556 0.6666667
 [8] 0.7777778 0.8888889 1.0000000

  [1] 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 0.11 0.12 0.13 0.14
 [16] 0.15 0.16 0.17 0.18 0.19 0.20 0.21 0.22 0.23 0.24 0.25 0.26 0.27 0.28 0.29
 [31] 0.30 0.31 0.32 0.33 0.34 0.35 0.36 0.37 0.38 0.39 0.40 0.41 0.42 0.43 0.44
 [46] 0.45 0.46 0.47 0.48 0.49 0.50 0.51 0.52 0.53 0.54 0.55 0.56 0.57 0.58 0.59
 [61] 0.60 0.61 0.62 0.63 0.64 0.65 0.66 0.67 0.68 0.69 0.70 0.71 0.72 0.73 0.74
 [76] 0.75 0.76 0.77 0.78 0.79 0.80 0.81 0.82 0.83 0.84 0.85 0.86 0.87 0.88 0.89
 [91] 0.90 0.91 0.92 0.93 0.94 0.95 0.96 0.97 0.98 0.99 1.00

  rep(3,10); rep(c(1,2,3,4,5),5)

 [1] 3 3 3 3 3 3 3 3 3 3

 [1] 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5

記号[ ]を使うと，ベクトルの要素を取り出すことができる．

  x <- seq(1,10,1)
  x[5]

[1] 5

これを使うと，ベクトルのある要素を他の値に変更することも可能となる．例えば次のコードを実行して確認してみよう．

  x <- seq(1,10,1)
  x[5] <- 10; x[10] <- 100
  x

 [1]   1   2   3   4  10   6   7   8   9 100

取り出す要素を複数指定することもできる．

  x <- seq(1,10,1)
  x[c(5,7,9)]

[1] 5 7 9

さらなる応用として，ある条件を満たす要素のみをベクトルから取り出すこともできる．その場合は基本的に条件式を利用する．

  x <- c(4,7,2,3,1,6,8,10,9,5)

  x <= 5; x < 5 ##  lower or equal, lower

 [1]  TRUE FALSE  TRUE  TRUE  TRUE FALSE FALSE FALSE FALSE  TRUE

 [1]  TRUE FALSE  TRUE  TRUE  TRUE FALSE FALSE FALSE FALSE FALSE

  x == 5 ## equal

 [1] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE

  x != 5 ## not equal

 [1]  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE FALSE

以上のコードを実行してみると，ベクトルの長さ分だけ，TRUEもしくはFALSEが出力されているのが確認できる．これを[ ]内に記述すると，TRUEに対応する要素だけをベクトルから取り出すことができる．

  x <- c(4,7,2,3,1,6,8,10,9,5)

  x[x <= 5]

[1] 4 2 3 1 5

  x[x == 5]

[1] 5

  x[x != 5]

[1]  4  7  2  3  1  6  8 10  9

ちなみに，関数whichを使うとTRUEの場所を返してくれる．

  x <- c(4,7,2,3,1,6,8,10,9,5)

  which(x <= 5)

[1]  1  3  4  5 10

  x[x <= 5]; x[which(x <= 5)]

[1] 4 2 3 1 5

[1] 4 2 3 1 5

Exercise 3.1

1から1000までの間の偶数と奇数をそれぞれ抽出せよ．

Exercise 3.2

数列(1,2,3,4,5,6,7,8,9,10)の中から3以上6未満の数字を取り出せ．

ヒント : 条件を組み合わせたいときは以下のように行う．

  5<2 && 3>2  ## 両方正しいかどうか判定

[1] FALSE

  5<2 || 3>2  ## 一方が正しいかどうか判定

[1] TRUE

ベクトルの演算と関数

ベクトル同士の演算や，ベクトルの数学関数を計算することもできる．

  x <- c(1,2,3); y <- c(4,5,6); z <- c(-2,4,-5)

  x + y; x - y; x * y; x / y; x ^ y

[1] 5 7 9

[1] -3 -3 -3

[1]  4 10 18

[1] 0.25 0.40 0.50

[1]   1  32 729

  4 * x; 10 * y

[1]  4  8 12

[1] 40 50 60

  sqrt(x); log(y)

[1] 1.000000 1.414214 1.732051

[1] 1.386294 1.609438 1.791759

  sign(z); abs(z)

[1] -1  1 -1

[1] 2 4 5

ベクトル全体に対する関数もRには用意されている．例えば，sumはベクトル内の全ての和を出力し，lengthはベクトルの長さを出力する．以下に，よく使う関数を列挙しておく．

  x <- c(4,7,2,3,1,6,8,10,9,5)

  sum(x); sqrt(sum(x^2)); mean(x) ## summation, norm, mean

[1] 55

[1] 19.62142

[1] 5.5

  length(x) ## length of x

[1] 10

  min(x); max(x) ## minimum and maximum

[1] 1

[1] 10

  which.min(x); which.max(x) ## 最小値(or 最大値)の場所を返す

[1] 5

[1] 8

Exercise 3.3

上記の例でwhich.minやwhich.max関数を使わずに同様のことを行ってみよ．

4. 行列

行列の生成

行列は基本的に2つの方法で作成できる．ひとつは，ベクトルを組み合わせて作る方法で，もうひとつは関数matrixを使う方法である．これは，matrix(要素, 行数, 列数)の形で記述する．次のコードを実行して，どんな行列が作成されるか確認しよう．

  x <- c(1,2); y <- c(3,4)

  cbind(x,y) ## ベクトルを横に並べる

     x y
[1,] 1 3
[2,] 2 4

  rbind(x,y) ## ベクトルを縦に並べる

  [,1] [,2]
x    1    2
y    3    4

  matrix(c(1,2,3,4),2,2)

     [,1] [,2]
[1,]    1    3
[2,]    2    4

  matrix(c(1,2,3,4,5,6),2,3)

     [,1] [,2] [,3]
[1,]    1    3    5
[2,]    2    4    6

  matrix(c(1,2,3,4,5,6),3,2)

     [,1] [,2]
[1,]    1    4
[2,]    2    5
[3,]    3    6

実行して分かるように，関数matrixのデフォルトでは要素を列順に格納していく．もし行順で格納したい場合は，byrow=TRUEというオプションを追加する．

  matrix(c(1,2,3,4,5,6),2,3,byrow=TRUE)

     [,1] [,2] [,3]
[1,]    1    2    3
[2,]    4    5    6

  matrix(c(1,2,3,4,5,6),3,2,byrow=TRUE)

     [,1] [,2]
[1,]    1    2
[2,]    3    4
[3,]    5    6

単位行列や対角行列であれば，簡単に生成できる．例えばp次元の単位行列はdiag(p)で生成でき，diag(対角成分)と記述すると，対角成分まで指定できる．

  diag(4)

     [,1] [,2] [,3] [,4]
[1,]    1    0    0    0
[2,]    0    1    0    0
[3,]    0    0    1    0
[4,]    0    0    0    1

  diag(c(1,2,3,4))

     [,1] [,2] [,3] [,4]
[1,]    1    0    0    0
[2,]    0    2    0    0
[3,]    0    0    3    0
[4,]    0    0    0    4

ベクトルのときと同じように，行列の特定の要素だけを取り出すことができる．ベクトルの場合と違うのは，行と列のふたつを指定する点である． A[i,j]で行列Aの第(i,j)成分，A[i,]で第i行， A[,j]で第j列を取り出すことが出来る．また，diag関数をある行列に対して使うと，その行列の対角成分だけを取り出すことができる．

  A <- matrix(c(1,2,3,4),2,2)

  A[1,2]; A[1,]; A[,2]

[1] 3

[1] 1 3

[1] 3 4

  diag(A)

[1] 1 4

Exercise 4.1

次の行列Aをオブジェクトとして用意し，その対角成分を対角要素に持つ行列Bを新たに作ってみよう．すなわち，行列Aから行列Bを作成してみよう．

\begin{align*} A= \begin{pmatrix} 3 & -6 & 8 \\ 3/2 & -1 & 9 \\ 11 & 4 & 1/5 \end{pmatrix} ,\quad B=\begin{pmatrix} 3 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0& 1/5 \end{pmatrix} \end{align*}

また，行列の行や列に名前をこともできる．行列Aの列名はcolnames(A)で取れるので，それに名前を付ければよい．行名に関してはrownames(A)を用いる．

  A <- matrix(c(1,2,3,4),2,2)
  colnames(A) <- c("1列","2列")
  rownames(A) <- c("1行","2行")
  A

    1列 2列
1行   1   3
2行   2   4

行列の演算

数値・ベクトル用の演算子を行列に使うとどうなるだろうか．

  A <- matrix(c(1,2,3,4),2,2); B <- matrix(c(5,6,7,8),2,2)

  A + B; A - B

     [,1] [,2]
[1,]    6   10
[2,]    8   12

     [,1] [,2]
[1,]   -4   -4
[2,]   -4   -4

  A * B; A / B; A ^ B

     [,1] [,2]
[1,]    5   21
[2,]   12   32

          [,1]      [,2]
[1,] 0.2000000 0.4285714
[2,] 0.3333333 0.5000000

     [,1]  [,2]
[1,]    1  2187
[2,]   64 65536

  A + 2; B - 2; A * 2; B / 5; A ^ 2

     [,1] [,2]
[1,]    3    5
[2,]    4    6

     [,1] [,2]
[1,]    3    5
[2,]    4    6

     [,1] [,2]
[1,]    2    6
[2,]    4    8

     [,1] [,2]
[1,]  1.0  1.4
[2,]  1.2  1.6

     [,1] [,2]
[1,]    1    9
[2,]    4   16

結果を見てみれば分かるように，数値・ベクトル用の演算子を使うと，要素ごとに演算が行われる．普通の行列の積を計算するためには，記号%*%を使う．

  A <- matrix(c(1,2,3,4),2,2); B <- matrix(c(5,6,7,8),2,2)
  A %*% B

     [,1] [,2]
[1,]   23   31
[2,]   34   46

Exercise 4.2

次の行列演算を実行せよ．

\begin{align*} \begin{pmatrix} 1 & 0 & 1 \\ 1 & 1 & 1 \\ 0 & 1 & 1 \end{pmatrix} \begin{pmatrix} 1\\ 4 \\ 2 \end{pmatrix},\quad \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \begin{pmatrix} 1 & 2 & 3 \end{pmatrix},\quad \begin{pmatrix} 4 & 5 & 6 \end{pmatrix} \begin{pmatrix} 4 \\ 5 \\ 6 \end{pmatrix} \end{align*}

行列に対する関数

Rには行列に対する演算がいくつか用意されている．例えば，転置行列は関数t，行列式はdet，逆行列はsolveで計算できる．

  A <- matrix(c(1,2,3,4),2,2)
  B <- matrix(c(1,2,2,1),2,2)

  t(A)

     [,1] [,2]
[1,]    1    2
[2,]    3    4

  det(A)

[1] -2

  solve(B)

           [,1]       [,2]
[1,] -0.3333333  0.6666667
[2,]  0.6666667 -0.3333333

行列の固有値を求める場合は，eigen関数を用いる．計算した固有値や固有ベクトルにアクセスするためには，$valuesや$vectorsを用いる．これは，後で紹介するリストという概念に関係している．関数eigenはリスト形式で結果を返しているのである．

  A <- matrix(c(1,2,2,1),2,2)
  B <- eigen(A)

  B$values

[1]  3 -1

  B$vectors

          [,1]       [,2]
[1,] 0.7071068 -0.7071068
[2,] 0.7071068  0.7071068

Rには階数を計算する関数が用意されていない．しかし，階数の性質を考えれば，固有値から簡単に計算ができる．

  A <- matrix(c(1,2,2,1),2,2)
  B <- eigen(A)
  sum(abs(sign(B$values))) ## rank of A

[1] 2

関数svdを使うと，行列のSVD分解を求めることができる．つまり，ある行列Aに対して，A=U\Lambda V^{T} となるような直交行列U,VおよびAの特異値を対角成分に持つ対角行列\Lambda に分解することができる．

  A <- matrix(c(1,2,2,1),2,2)
  B <- svd(A)
  U <- B$u; V <- B$v; Lam <- diag(B$d)
  U %*% Lam %*% t(V) ## (= A)

     [,1] [,2]
[1,]    1    2
[2,]    2    1

apply関数

行列の行もしくは列ごとに，sumなどの関数を適用する際には，apply関数と用いる．これは，apply(matrix, margin, function)の形で記述する． marginの部分には，1もしくは2を代入し，1であれば行に関して，2であれば列に関して関数を適用することを意味する．例えば次のコードを実行して，結果を確認してみよう．

  A <- matrix(c(1,2,3,4),2,2)

  apply(A,2,sum); apply(A,1,sum)

[1] 3 7

[1] 4 6

  apply(A,2,mean); apply(A,1,mean)

[1] 1.5 3.5

[1] 2 3

ちなみに，関数meanは平均値を計算する関数で， applyと組み合わせると，データ行列に対して各変数の平均値を計算することができる．他にも，関数varやsdなどがあり，それぞれ分散と標準偏差を計算する関数である．

似た関数に，sweep関数というものがある．これは，各行または列に対して，ベクトルを足す・引く・掛ける・割るための関数である．

  A <- matrix(c(1,2,3,4),2,2)
  a <- c(1,2)

  sweep(A,1,a,FUN="+"); sweep(A,1,a,FUN="-")

     [,1] [,2]
[1,]    2    4
[2,]    4    6

     [,1] [,2]
[1,]    0    2
[2,]    0    2

  sweep(A,2,a,FUN="*"); sweep(A,2,a,FUN="/")

     [,1] [,2]
[1,]    1    6
[2,]    2    8

     [,1] [,2]
[1,]    1  1.5
[2,]    2  2.0

Exercise 4.3

次のデータは北京のアメリカ大使館で2014年4月1日12時から18時に観測された pm2.5, 気温, 風速である．このデータをRに入力し，apply関数を利用してそれぞれの平均, 分散, 標準偏差を求めよう．

時刻	pm2.5	気温	風速
12:00	121	21	3.57
13:00	124	23	3.13
14:00	94	24	3.13
15:00	63	24	4.92
16:00	52	24	10.73
17:00	64	24	16.54
18:00	48	22	20.56

Exercise 4.4

apply関数を使わずに，sweep関数を用いて上記のデータ行列の列ごとの分散を計算してみよ．

5. リスト

list関数を使うと，行列，ベクトル，数値などをひとまとまりとして扱うことができる．list(A,b,c)のようにして記述する．

  A <- matrix(c(1,2,3,4),2,2); b <- c(3,6,9); c <- 100
  list(A,b,c)

[[1]]
     [,1] [,2]
[1,]    1    3
[2,]    2    4

[[2]]
[1] 3 6 9

[[3]]
[1] 100

リストの要素へアクセスするためには，二重括弧[[ ]]と括弧[ ]を合わせて用いる．また，リストには名前を付けることも可能で，その名前を使ってリストにアクセスできるようになる．

  A <- matrix(c(1,2,3,4),2,2); b <- c(3,6,9); c <- 100
  Li <- list(A,b,c)

  Li[[1]]; Li[[3]]; Li[[2]][3]

     [,1] [,2]
[1,]    1    3
[2,]    2    4

[1] 100

[1] 9

  names(Li) <- c("mat", "vec", "val")
  Li$mat; Li$val; Li$vec[3]

     [,1] [,2]
[1,]    1    3
[2,]    2    4

[1] 100

[1] 9

6. データフレーム

データフレームは，その要素に様々なデータ型(日時，数値，文字など)を内包できるため，データ解析において頻繁にあらわれる．基本的な作り方は以下のようになる．

  mydf <- data.frame(
      名前 = c("Aさん", "Bさん", "Cさん", "Dさん"),
      性別 = c("女性", "男性", "女性", "男性"),
      記録 = c(110,120,109,144),
      記録日時 = c("2023-11-01","2023-11-02","2023-11-04","2023-11-10")
      )
  mydf

   名前 性別 記録   記録日時
1 Aさん 女性  110 2023-11-01
2 Bさん 男性  120 2023-11-02
3 Cさん 女性  109 2023-11-04
4 Dさん 男性  144 2023-11-10

mydfの2行目をみると，いくつかのデータ型が内包されているのが確認できる．chrは文字列型で，dblは実数値型である．もう少しデータを扱いやすくするために，性別をラベル型(factor型)に，記録日時を日付型に変更してみる．

  mydf2 <- data.frame(
      名前 = c("Aさん", "Bさん", "Cさん", "Dさん"),
      性別 = as.factor(c("女性", "男性", "女性", "男性")),
      記録 = c(110,120,109,144),
      記録日時 = as.Date(c("2023-11-01","2023-11-02","2023-11-04","2023-11-10"))
      )
  mydf2

   名前 性別 記録   記録日時
1 Aさん 女性  110 2023-11-01
2 Bさん 男性  120 2023-11-02
3 Cさん 女性  109 2023-11-04
4 Dさん 男性  144 2023-11-10

データフレームの要素へのアクセスは，行列のときのようにも出来るし，名称を指定することでも出来る．

  mydf2[1,2]  #(1,2)要素の取り出し

[1] 女性
Levels: 女性 男性

  mydf2[,3]  #3列の取り出し

[1] 110 120 109 144

  mydf2[1:2,]  #最初の2行

   名前 性別 記録   記録日時
1 Aさん 女性  110 2023-11-01
2 Bさん 男性  120 2023-11-02

  mydf2$名前  #名前列の取り出し

[1] "Aさん" "Bさん" "Cさん" "Dさん"

  mydf2$記録日時[4]  #Dさんの記録日時

[1] "2023-11-10"

7. 乱数の発生

乱数は，検定を行う場合や，シミュレーションを行う場合に重宝される． Rでは様々な分布に従う乱数を簡単に生成することができる．先ずは正規乱数から紹介する．これはrnormを使えばOKで，書き方は，rnorm(サイズ, 平均, 標準偏差)．

  rnorm(10, 0, 1) #10個の標準正規乱数を発生

 [1]  0.4283771  0.4694416 -0.8346548 -0.7816836  0.1331051 -1.1545172
 [7] -1.8575962  0.8180407 -2.0847330  0.3165522

ちなみに，先頭の文字rをd，p，qと変更することで，確率密度f(x)，累積分布\mathbb{P}(X\le x)，確率点F^{-1}(p)を計算することができる．次のコードで確認してみよう．

  dnorm(0)  ## f(0)

[1] 0.3989423

  pnorm(1.6448)  ## P(X <= 1.6448) where X is drawn from N(0,1)

[1] 0.9499945

  qnorm(0.80)  ## F^{-1}(0.80)

[1] 0.8416212

後半の文字normを変更すると，正規分布以外の分布から乱数の生成や，確率密度の計算などができる．よく使いそうな分布を下記にまとめておく．詳細はヘルプなどの参照のこと．

分布	関数
二項分布	`binom`
多項分布	`multinom`
ポアソン分布	`pois`
負の二項分布	`nbinom`
一様分布	`unif`
指数分布	`exp`
t分布	`t`
\chi^{2}分布	`chi`

8. 構文

制御構文

条件分岐のためにはif構文を使う．先ずは簡単な構文，xが5以下の場合に処理を実行するコードを書いてみる． ifの後に条件を記述し，それが真であれば次の行から実行される．以下によく用いられる条件式をまとめておく．

記号	意味
==	equal
!=	not equal
in	in a set
<	<
<=	\le
>	>
>=	\ge

  x <- 3
  if(x <= 5){
    print("x is less than or equal to 5")
  }

[1] "x is less than or equal to 5"

x \le 5が満たされない場合は何も実行されない．

  x <- 10
  if(x <= 5){
     print("x is less than or equal to 5")
  }

else関数を使うと，条件が満たされない場合の処理を記述することができる．そして，else if関数を使うと，複数の条件を記述することができる．

  x <- 3
  if(x <= 5){
     print("x is less than or equal to 5")
  } else {
     print("x is larger than 5")
  }

[1] "x is less than or equal to 5"

  x <- 100
  if(x <= 5){
      print("x is less than or equal to 5")
  } else {
      print("x is larger than 5")
  }

[1] "x is larger than 5"

  x <- 2
  if(x == 0){
      print("x is equal to 0") 
  } else if(x == 1){
      print("x is equal to 1") 
  } else if(x == 2){
      print("x is equal to 2")
  } else {
      print("x is other than 0,1 or 2")
  }

[1] "x is equal to 2"

繰り返し構文

繰り返し構文にはfor関数やwhile関数を用いる．次のコードは10次元のベクトルにそれぞれ値を代入していくものである．

  x <- rep(0,10) ## 箱を用意
  for(i in 1:10){  ## for(条件式)のように記述する
      x[i] <- 100*i  ## xの要素iに100*iを代入
  }
  x

 [1]  100  200  300  400  500  600  700  800  900 1000

これをwhile関数を用いて書くと次のようになる．

  x <- rep(0,10)
  i <- 1 ## 繰り返し回数の初期値
  while(i <= 10){ ## i が 10 以下の場合は繰り返す
      x[i] <- 100*i
      i <- i + 1 ## 繰り返し回数をカウント
  }
  x

 [1]  100  200  300  400  500  600  700  800  900 1000

repeat関数を使って繰り返し処理を行うこともできる．この関数は，breakが現れるまでずっと繰り返しを行う．そのため，repeat関数を使う場合は無限回の繰り返しにならないように注意が必要である．もし無限回の繰り返しを実行してしまった場合は，Rコンソールの上部にあるStopボタンを押せばOK.

  x <- rep(0,10) 
  i <- 1  
  repeat{
      if(i <= 10){
          x[i] <- 100*i
      } else break
      i <- i + 1 
  }
  x

 [1]  100  200  300  400  500  600  700  800  900 1000

Exercise 8.1

区間(0,1)の一様分布から1000個独立に乱数を発生させ，それぞれx_{i}\;(i=1,2,\dots, 1000)とおく．このとき，数列(y_{1},y_{2},\dots, y_{1000})を発生させよ．ただし，

y_{i}=\begin{cases} 1, & x_{i} \le 0.3 \\ 0, & x_{i} > 0.3 \end{cases}

とする．また，発生させた数列\{y_{i}\}の平均がおおよそ0.3であること(why?)を確認せよ．

9. 自作関数

Rではsum関数やmean関数などの，用意された関数の他に，自分で関数を作成することができる．そのためにはfunctionを使って， function(引数1, 引数2,...)のように記述する．次のコードは，引数をxとしてy=e^{-x^{2}/2}を出力するmyfunction1という関数を定義するものである．

  myfunction1 <- function(x){ 
      y <- exp(-x^(2)/2)
      return(y) 
  }

  myfunction1(0.1)

[1] 0.9950125

  myfunction1(seq(0.1,1,length=10))  ## ベクトルを引数にしている

 [1] 0.9950125 0.9801987 0.9559975 0.9231163 0.8824969 0.8352702 0.7827045
 [8] 0.7261490 0.6669768 0.6065307

実行してみると分かるように，引数としてベクトルも使うことができて，要素ごとの関数値が計算される．一般的に行列(リストも)を引数することもできる．ただし注意が必要で，ベクトルを適切に処理できるように関数を定義する必要がある．上記のコードでは，指数関数や2乗が，要素ごとに処理されるため，問題はない．しかし次のコードだと，ベクトルを引数にした場合はエラーを返す．

  myfunction2 <- function(x){ 
      if(abs(x) <= 1){
          y <- 0 
      } else {
          y <- x
      }
      return(y)
  }

  myfunction2(0.5)

[1] 0

  myfunction2(c(0.5,1,2))

Warning in if (abs(x) <= 1) {: 条件が長さが 2 以上なので、最初の 1 つだけが使わ
れます

[1] 0

このように，値だけしか引数にできない関数を，ベクトルの要素ごとに適用するためには，sapply関数が有効である．次のコードを実行して確認してみよう．

  sapply(seq(0,2,length=20),function(x){myfunction2(x)})

 [1] 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000
 [9] 0.000000 0.000000 1.052632 1.157895 1.263158 1.368421 1.473684 1.578947
[17] 1.684211 1.789474 1.894737 2.000000

もし自作関数に引数が複数あった場合も，sapply関数を利用できる．

  myfunction3 <- function(x,a){
      y <- exp(-x^(2)/(2*a)) 
      return(y) 
  }

  sapply(seq(0,2,length=20),function(x){myfunction3(x,a=1)})

 [1] 1.0000000 0.9944752 0.9780831 0.9513612 0.9151725 0.8706596 0.8191845
 [8] 0.7622596 0.7014746 0.6384235 0.5746371 0.5115243 0.4503258 0.3920805
[15] 0.3376071 0.2874986 0.2421295 0.2016729 0.1661252 0.1353353

  sapply(seq(0,2,length=20),function(x){myfunction3(x,a=2)})

 [1] 1.0000000 0.9972338 0.9889808 0.9753775 0.9566465 0.9330914 0.9050881
 [8] 0.8730748 0.8375408 0.7990141 0.7580482 0.7152093 0.6710632 0.6261633
[15] 0.5810396 0.5361889 0.4920666 0.4490801 0.4075845 0.3678794

10. 図のプロット

単純な図のプロット

例えば次の2次元データが与えられているとする．

  data.frame(x=1:8,y=(1:8)^2)

Rを使ってデータをプロットするためには，plot関数を利用する．基本的には，xとyにデータをベクトル形式で代入して，plot(x,y)を実行すると自動的にプロットされる．オプションも追加できる．以下では簡単に紹介するが，より詳細を知りたければ，par関数のヘルプを見てほしい.

  x <- 1:8; y <- x^2
  plot(x, y, xlim=c(0,9), ylim=c(0,70), type="l", lwd=2, col="blue", main="main_title", xlab="x_label", ylab="y_label")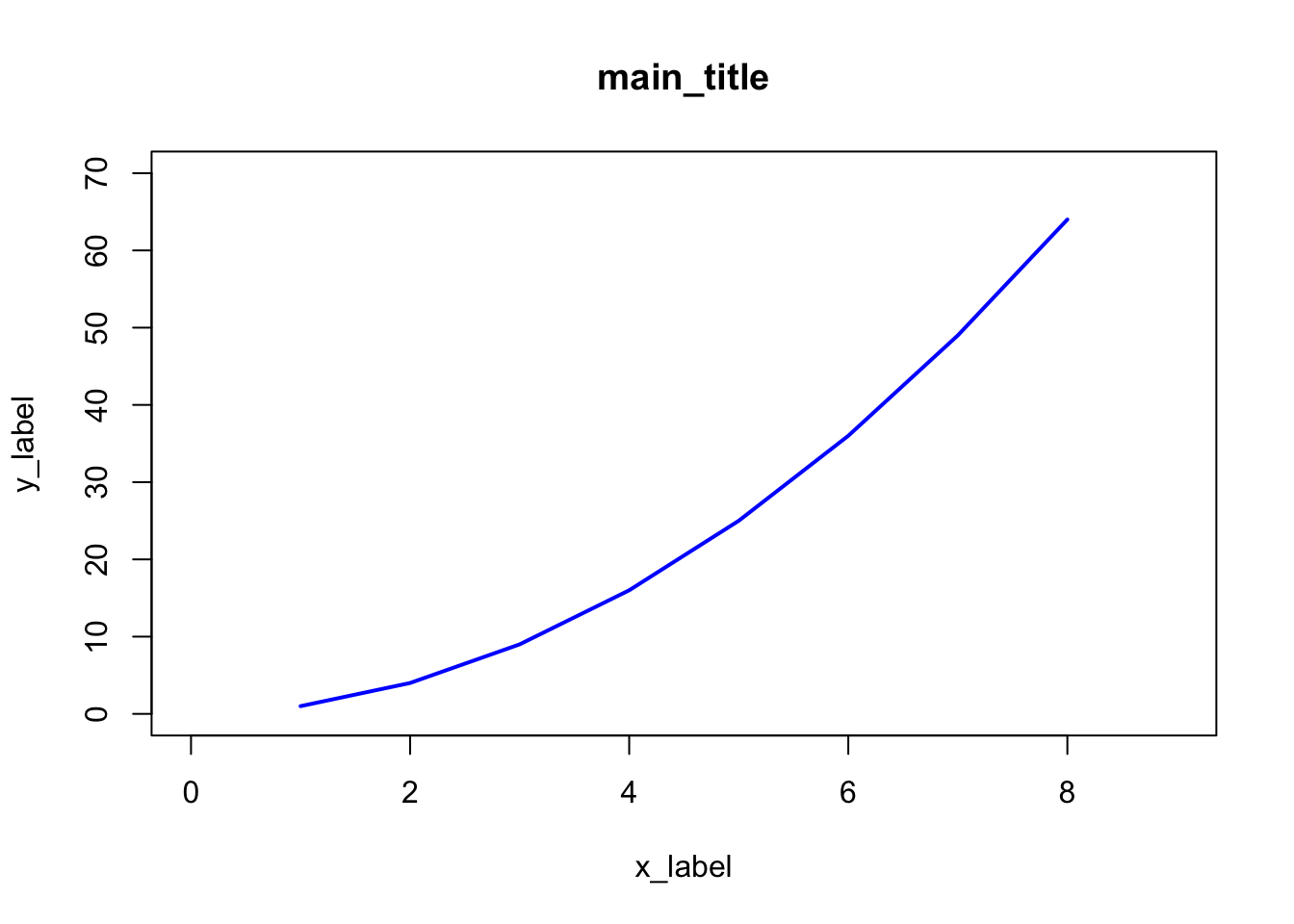

いくつかのオプション :

記号	意味
xlim	x軸のプロット範囲を指定する
ylim	y軸のプロット範囲を指定する
type	プロットの種類を指定する．たとえば`l`は線，`p`は点，`b`は点と線
lwd	線の太さを指定する．値が大きいほど太い
col	色の指定をする．`blue`,`green`,`red`などがある．数値でも可
main	グラフのタイトルを指定する．タイトルを付けたくなければ`main=""`とする
xlab	x軸のタイトルを指定する
ylab	y軸のタイトルを指定する

関数をプロットするためにはcurve関数を用いる．

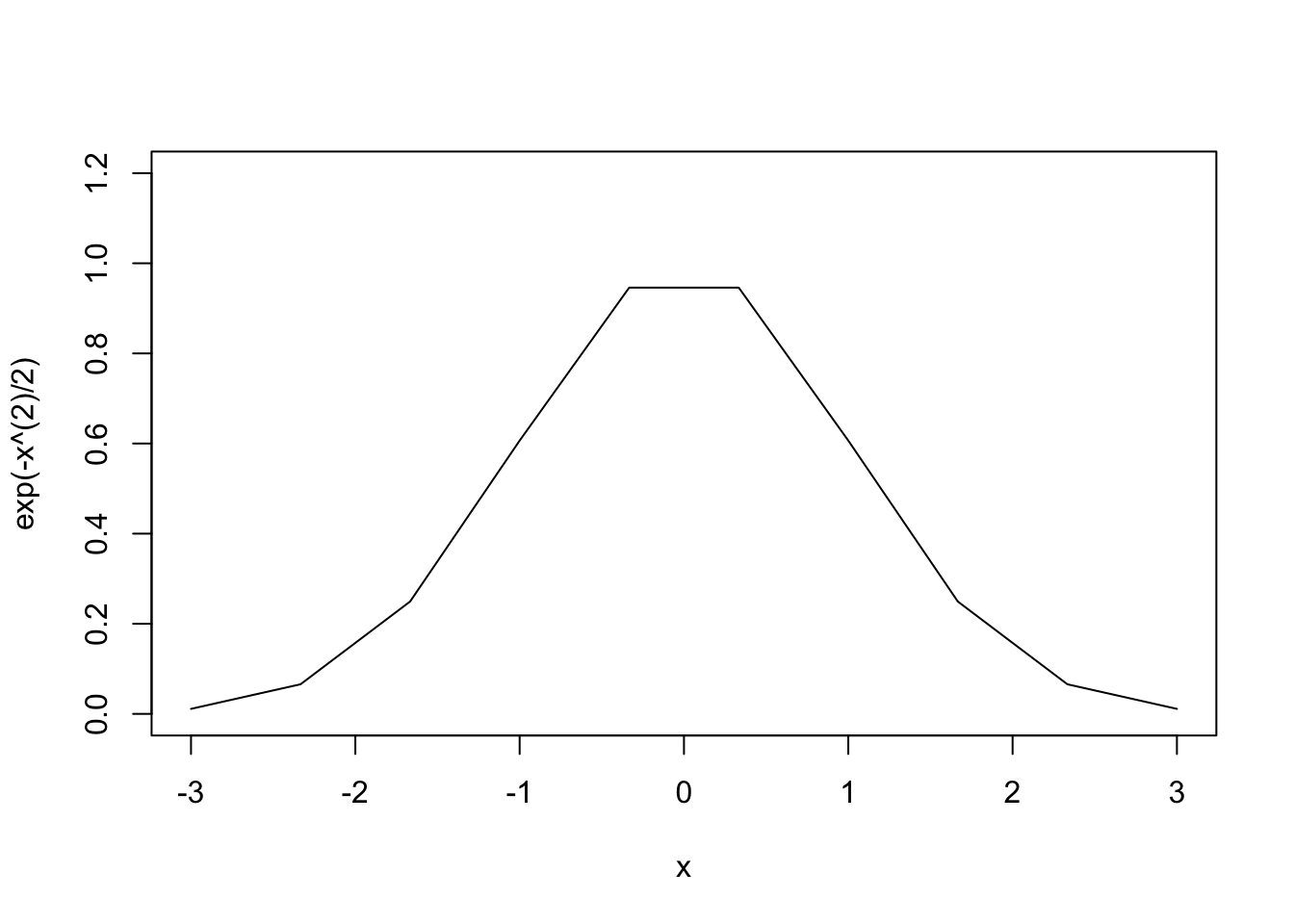
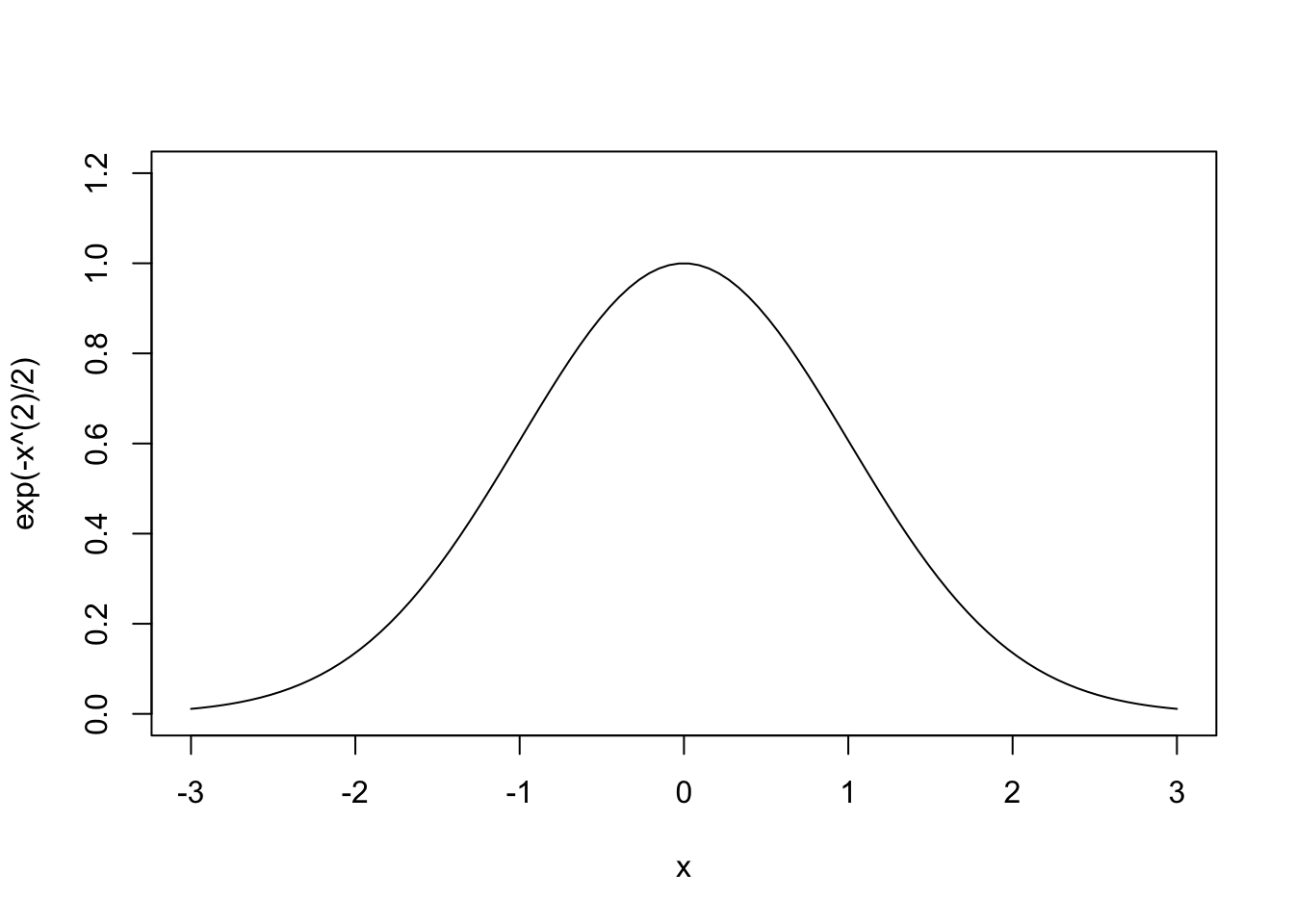
  curve(exp(-x^(2)/2), from=-3, to=3, n=10, xlim=c(-3,3), ylim=c(0,1.2))

  curve(exp(-x^(2)/2), from=-3, to=3, n=100, xlim=c(-3,3), ylim=c(0,1.2))

オプションnでプロットのときに使う点の個数を指定できる．この値が大きなほど高精細なグラフが描けるが，大きくしすぎると計算に時間がかかってしまう．

Exercise 10.1

plot関数を使ってsin(x)を-1\le x\le 1の範囲でプロットしてみよう．ただし，ある程度滑らかに表示すること．

複数グラフの重ね合わせ

複数のグラフを同じ領域の中に描くこともできる．par(new=T)をプロットとプロットの間に記述すると，同じ描写領域の中に，重ね書きをしてくれる．ただし，軸やラベルも重ね書きされることに注意．軸を消すためには，plot(or curve)のオプションにann=Fを追加する．また，Rが自動的に軸の範囲を指定する場合もあるので，範囲を全てのプロットで揃えておかなければならない.

  curve(exp(-x^(2)/2), from=-3, to=3, n=100, xlim=c(-3,3), ylim=c(0,1.2)) 
  par(new=T)  ## 重ね書き
  curve(exp(-x^(2)/1), from=-3, to=3, n=100, xlim=c(-3,3), ylim=c(0,1.2), ann=F, col="blue", xlab="", ylab="")  ## xlimとylimは揃えて、ラベルをann=Fで消しておく
  par(new=T)  ## 重ね書き
  curve(exp(-x^(2)/0.5), from=-3, to=3, n=100, xlim=c(-3,3), ylim=c (0,1.2), ann=F, col="red", xlab="", ylab="")
  legend("topright", legend=c("var1", "var1/2", "var1/4"), lty=1, col=c(" black", "blue", "red"))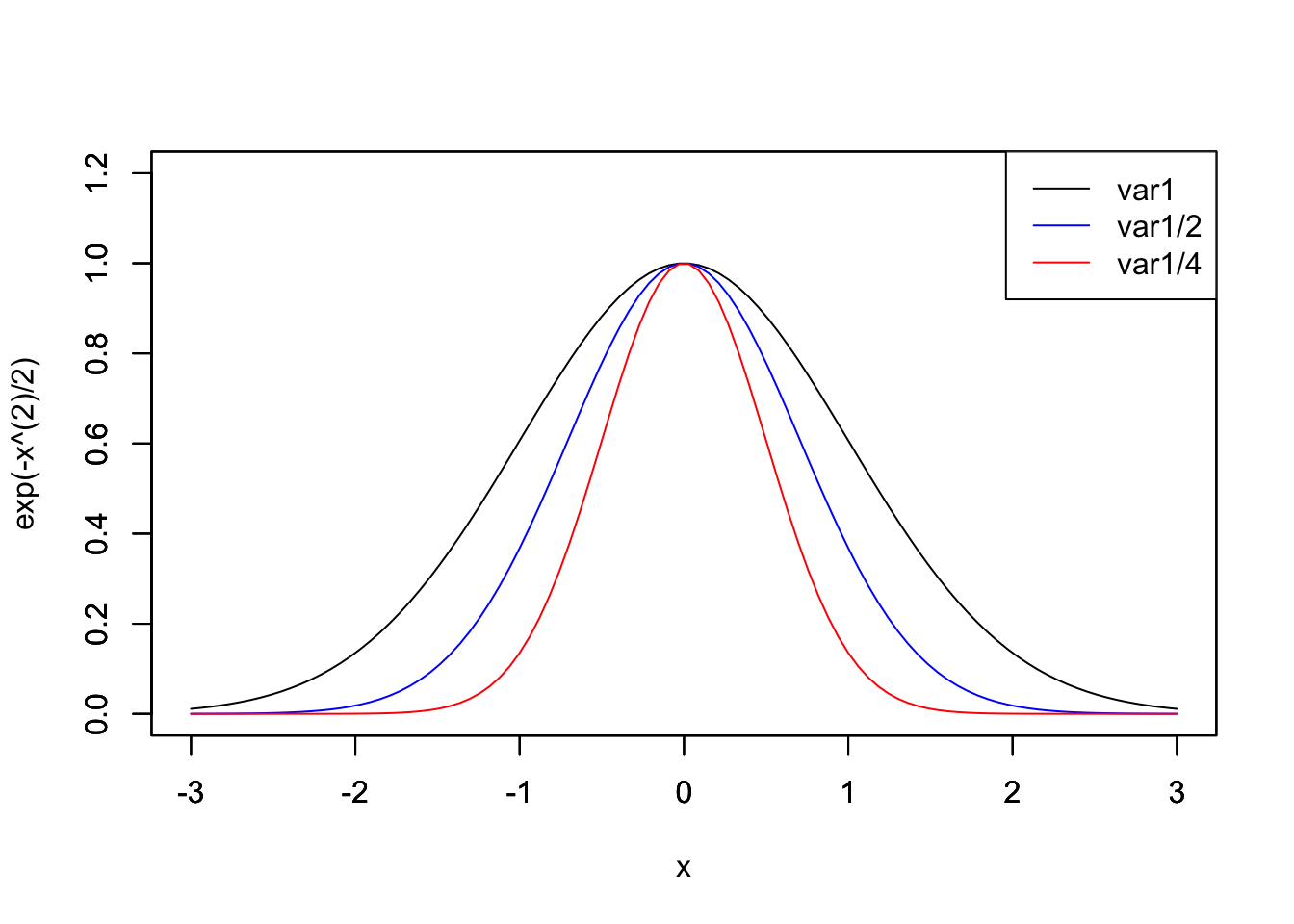

上のコードで，関数legendはグラフの凡例を追加している．最初のオプションは凡例の場所を指定する．座標でも指定できるが，topright,topleft,bottomright,bottomleftのように指定する方が簡単である．legendではグラフの名前を指定，ltyでは線の種類を指定(数字を変えてみよう)している．legendの前にはpar(new=T)と記述する必要はない．それ単体で重ね合わせをしてくれる．このようなものは他にも，abline関数がある．abline(a,b)で関数y = a + bxが，abline(v = x)でxを通る垂直線が描かれる.

  curve(exp(-x^(2)/2), from=-3, to=3, n=100, xlim=c(-3,3), ylim=c(0,1.2)) 
  abline(0,0,col="blue")
  abline(v = 0,col="red")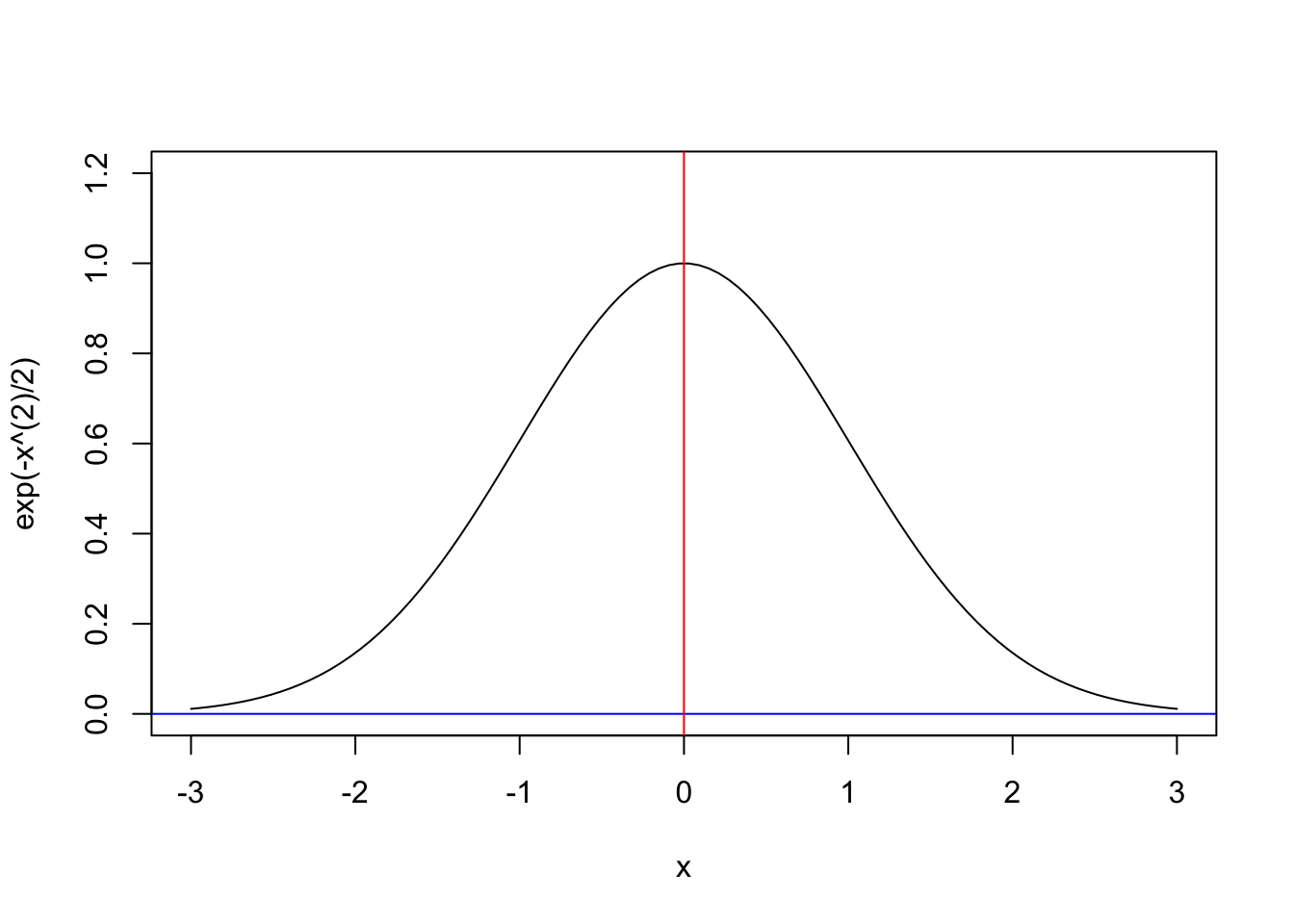

関数形ではなく，適当なデータを複数プロットするには，matplotを使った方が簡単である．これはある行列Xの各列についてプロットを行うための関数である．適当なデータ行列に対して，各変数ごとにグラフを描きたい場合などにも重宝される.

  x <- seq(1,10, length=20) 
  y <- x^2
  w <- x^(2.3)
  z <- x^(2.5)
  X <- cbind(y,w,z) ## 行列 (or データ行列) X
  matplot(x, X, type="o", pch=1:3, lty=1:3, col=1:3, xlab="", ylab="") 
  legend("topleft", legend=c("x^2","x^2.3","x^2.5"), lty=1:3, pch=1:3, col=1:3)

グラフを並べる

複数のプロット図を並べたい場合もあるだろう．その場合は，プロットを行う前に，描写領域を分割しておく必要がある．そのためには，par(mfcol=c(m,n))もしくはpar(mfrow=c(m,n))と書けばOK．これは描写領域をm \times nに分割するためのコードである．mfcolで指定した場合は列順に，mfrowの場合は行順に描写が行われる.

  x <- seq(1,10, length=20) 
  y <- x^2
  v <- x^(2.1)
  w <- x^(2.3)
  z <- x^(2.5)
  par(mfrow=c(2,2)) ## let’s try mfcol=c(2,2)
  plot(x,y,main=1); plot(x,v,main=2); plot(x,w,main=3); plot(x,z,main=4)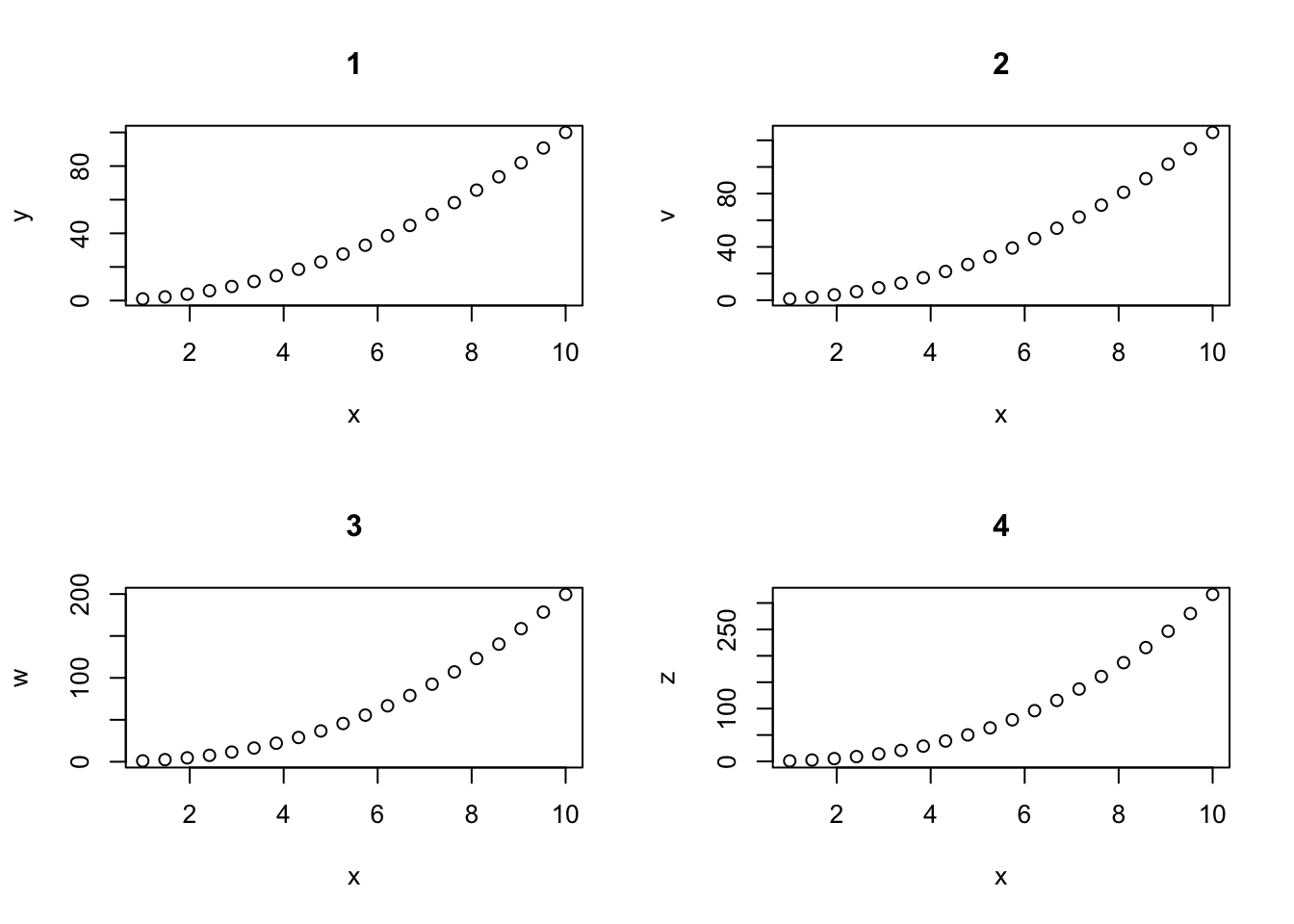

Exercise 10.2

正規分布の確率密度関数は以下で定義される．

f(x)=\frac{1}{\sqrt{2\pi\sigma^{2}}}\exp\bigg\{-\frac{(x-\mu)^{2}}{2\sigma^{2}}\bigg\}, \quad x\in\mathbb{R}

このとき，plot関数を用いて(\mu,\sigma^{2}) = (0,1), (0,0.1), (0,5), (2,0.5)に対する正規分布の密度関数を同じ領域の中に描写せよ．ただし，x軸の範囲は-5\le x\le 5とし，それぞれの関数は異なる色で描くこと．そして対応する適切な判例を領域の左上に表示すること．なお，円周率\piはR上ではpiで計算される．

その他のグラフ

棒グラフを描くためにはbarplot，ヒストグラムを描くためにはhist，箱ひげ図を描くためにはboxplotをそれぞれ使う．

  pm25 <- c(121,124,94,63,52,64,48)
  temp <- c(21,23,24,24,24,24,22)
  time <- c("12:00","13:00","14:00","15:00","16:00","17:00","18:00")

  par(mfrow=c(1,3))
  barplot(temp, names.arg=time, xlab="time", ylab="temp") ##棒グラフ 
  hist(pm25) ##ヒストグラム
  boxplot(pm25) ##箱ひげ図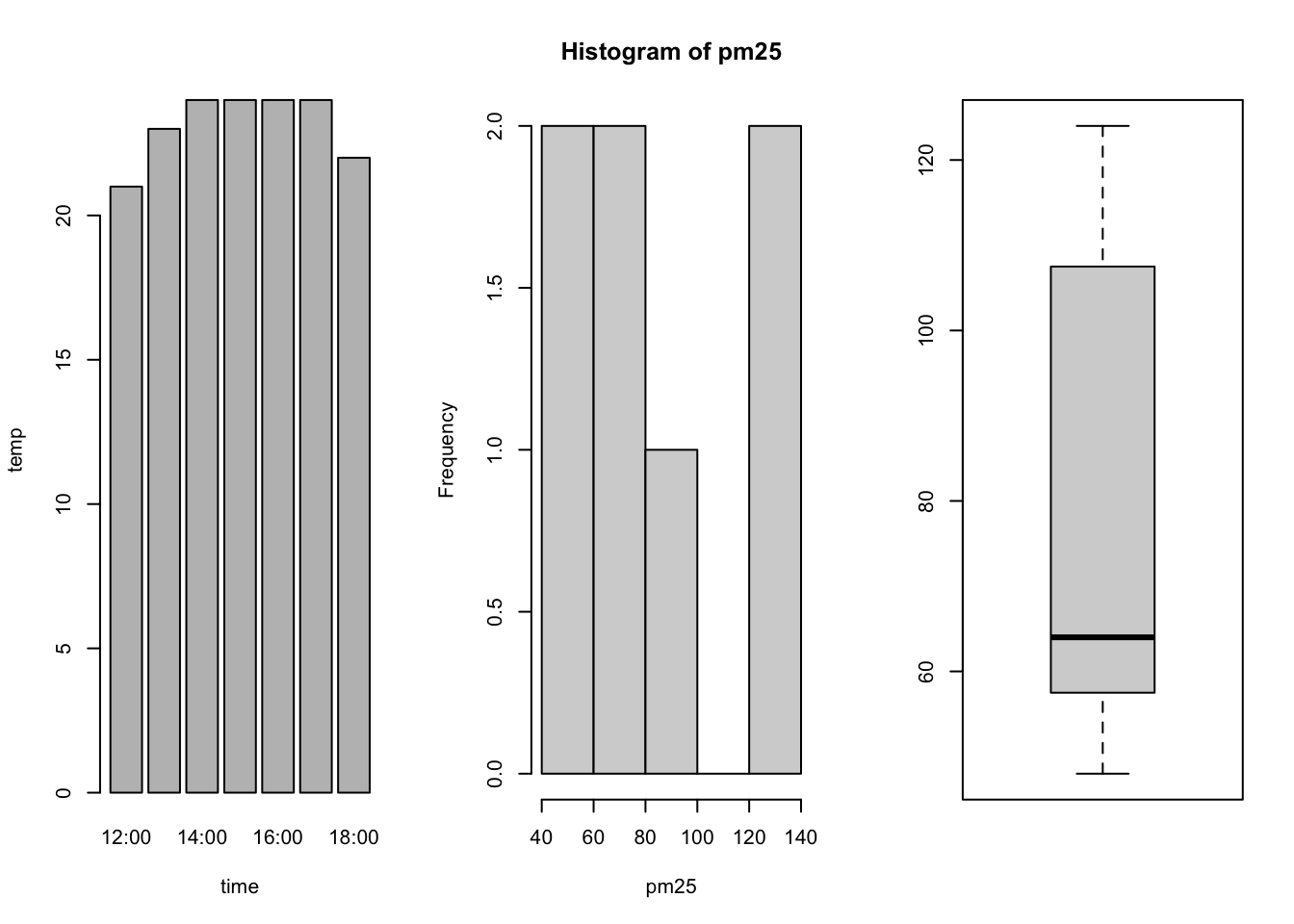

複数の箱ひげ図を描写したい場合はboxplot(list(data1,data2))のように描く．listではなく行列で入力してもok．その場合は列ごとに箱ひげ図が描写される．

  par(mfrow=c(1,2))
  boxplot(list(rnorm(100,0,1), rnorm(100,0,2), rnorm(100,0,3)))
  boxplot(cbind(rnorm(100,0,1), rnorm(100,0,2), rnorm(100,0,3)))

11. 簡単なデータ解析

データの読み込み(csvファイルから)

先ずデータをcsv形式で用意する．テキスト形式でも読み込むことができるが，csv形式の方がExcelから変換できるので簡単である．今回は，UCI Machine Learning Repositoryから白ワインのグレードに関するデータを持ってこよう.

http://archive.ics.uci.edu/ml/datasets/Wine+Quality

上記サイトのData Folderからwinequality-white.csvをダウンロードしよう．次に現在の作業ディレクトリをgetwd()で確認し，適宜setwd()で作業ディレクトリを適当なフォルダに変更する．最後に作業ディレクトリにダウンロードしたファイルを置いておく．

  X <- read.csv("winequality-white.csv", header=T,sep=";")
  n <- dim(X)[1]; p <- dim(X)[2] ## sample size and dimension 
  var <- names(X) ##変数名

headerというオプションは，第1行目に変数の名前が書かれているかどうかを指定するものである．今回は書かれているので，Tと指定する．第1行目が変数の名前なのに，Fと指定するとおかしなことになる．

sepはデータ区切りの記号を指定する関数である．上のコードを実行すると分かるように，Xはデータ数4898(白ワインの数)，次元12のデータ行列である.変数の名前はvarに格納している．

第1変数から第11変数までが，白ワインの特徴(各種濃度とかアルコール量)を計測したもので，第12変数quolityが，白ワインの質を専門家が評価した値である．0だとまずく，10だとうまい．データ数が大きいので，全部をコンソール上に表示すると大変なことになる．その場合はhead関数が便利で，これは最初の数行を表示してくれる．

  head(X)

  fixed.acidity volatile.acidity citric.acid residual.sugar chlorides
1           7.0             0.27        0.36           20.7     0.045
2           6.3             0.30        0.34            1.6     0.049
3           8.1             0.28        0.40            6.9     0.050
4           7.2             0.23        0.32            8.5     0.058
5           7.2             0.23        0.32            8.5     0.058
6           8.1             0.28        0.40            6.9     0.050
  free.sulfur.dioxide total.sulfur.dioxide density   pH sulphates alcohol
1                  45                  170  1.0010 3.00      0.45     8.8
2                  14                  132  0.9940 3.30      0.49     9.5
3                  30                   97  0.9951 3.26      0.44    10.1
4                  47                  186  0.9956 3.19      0.40     9.9
5                  47                  186  0.9956 3.19      0.40     9.9
6                  30                   97  0.9951 3.26      0.44    10.1
  quality
1       6
2       6
3       6
4       6
5       6
6       6

逆にR上で作成したデータをcsvファイルに出力するためにはwrite.csv関数を用いる．

基本統計量の計算

白ワインデータの，各変数に対する平均値，標準偏差，最大値，最小値を計算してみよう．これには前述のapply関数を使うとできる．

  means <- apply(X, 2, mean) 
  sds <- apply(X, 2, sd) 
  maxes <- apply(X, 2, max) 
  mins <- apply(X, 2, min)

箱ひげ図を書いてみるのもひとつの手段．これはboxplot関数でできる．引数はベクトルでも行列でもどちらでもよい．

  par(mfrow=c(1,2))
  boxplot(X[,1]) 
  boxplot(X)

変数間の関連性を見たい場合は，共分散行列か相関行列を計算すればOK．これは共分散行列はvar関数で，相関行列はcor関数で計算できる．

  covmat <- var(X)
  cormat <- cor(X)

散布図行列を確認するのもひとつの手段．これはpairs関数でプロットできる．今回は後半の変数だけでプロットしてみる．

  pairs(X[,6:12])

Exercise 11.1

関数varやcorを使わずに共分散行列や相関行列を計算せよ．

Exercise 11.2

箱ひげ図や最大値・最小値などを使って，おかしな特徴値を取っているワイン(外れ値)を特定せよ．

12. ライブラリの使い方

Rにはライブラリという便利な拡張機能がある．目的に応じたパッケージを読み込むことで，自分でプログラミングする必要なしに，様々な事が1 行程度で実行できる．まずはパッケージを自分のコンピュータの中にインストールしよう． - (Windowsの場合) パッケージ -> パッケージのインストールの順にクリック．サーバを選び，目的のパッケージをインストールする．追加パッケージが必要な場合はそれらも全てインストールする． - (Macの場合) パッケージとデータ -> パッケージインストーラの順にクリック．一覧を取得ボタンを押し，目的のものをインストール．その際，依存パッケージも含めるにチェックを入れておく．目的のパッケージがインストールできたら，次はRにそれを読み込むため，library関数を利用する．

例えばサポートベクトルマシン(SVM)を実行したい場合は，パッケージe1071をインストールし，次のように入力する．

  library(e1071) ## パッケージをロードする

  X <- read.csv("winequality-white.csv", header=T,sep=";")  ## データの読み込み

  wine.svm <- svm(quality~., data=X[1:4000,]) ## SVMの実行
  wine.pre <- predict(wine.svm,X[4001:4898,-12]) ## SVMによるqualityの予測
  table(X[4001:4898,12],round(wine.pre)) ## 真の結果と予測結果

   
      4   5   6   7
  3   0   1   0   0
  4   2  11   8   0
  5   2 129 108   4
  6   0  50 328 103
  7   0   0  64  69
  8   0   0  12   7

株価データの読み込み

パッケージquantmodおよびXMLをインストールして読み込む．

  library(quantmod)

 要求されたパッケージ xts をロード中です

 要求されたパッケージ zoo をロード中です


 次のパッケージを付け加えます: 'zoo'

 以下のオブジェクトは 'package:base' からマスクされています: 

     as.Date, as.Date.numeric

 要求されたパッケージ TTR をロード中です

Registered S3 method overwritten by 'quantmod':
  method            from
  as.zoo.data.frame zoo

  library(XML)

Yahoo Financeから任天堂(コード7974.t)の株価データを取得する．コードは各証券ページに記載がある．

  nintendo <- getSymbols("7974.t", src = "yahooj", from = "2024-01-01", to = "2024-04-10", auto.assign=FALSE)

  head(nintendo)

           YJ7974.T.Open YJ7974.T.High YJ7974.T.Low YJ7974.T.Close
2024-01-04          7227          7274         7138           7176
2024-01-05          7202          7290         7197           7223
2024-01-09          7305          7568         7290           7538
2024-01-10          7646          7902         7622           7823
2024-01-11          7928          8075         7841           7930
2024-01-12          8010          8180         7960           8125
           YJ7974.T.Volume YJ7974.T.Adjusted
2024-01-04         5215500              7176
2024-01-05         4107700              7223
2024-01-09         6863600              7538
2024-01-10         9140900              7823
2024-01-11         9331400              7930
2024-01-12         9141400              8125

  dnintendo <- fortify.zoo(nintendo)  ##dataframeに変換する．パッケージzooの関数fortify.zooを利用
  names(dnintendo) <- c("data","open","high","low","close","volume","adjusted")

  head(dnintendo)

        data open high  low close  volume adjusted
1 2024-01-04 7227 7274 7138  7176 5215500     7176
2 2024-01-05 7202 7290 7197  7223 4107700     7223
3 2024-01-09 7305 7568 7290  7538 6863600     7538
4 2024-01-10 7646 7902 7622  7823 9140900     7823
5 2024-01-11 7928 8075 7841  7930 9331400     7930
6 2024-01-12 8010 8180 7960  8125 9141400     8125