単回帰分析
ISLRパッケージ内のAutoデータを読み込む.これは392の車種に対する走行距離mpg,馬力horsepower,重さweightなどのデータである.
mpg cylinders displacement horsepower weight acceleration year origin
1 18 8 307 130 3504 12.0 70 1
2 15 8 350 165 3693 11.5 70 1
3 18 8 318 150 3436 11.0 70 1
4 16 8 304 150 3433 12.0 70 1
5 17 8 302 140 3449 10.5 70 1
6 15 8 429 198 4341 10.0 70 1
name
1 chevrolet chevelle malibu
2 buick skylark 320
3 plymouth satellite
4 amc rebel sst
5 ford torino
6 ford galaxie 500
結果変数を走行距離mpg,説明変数を馬力horsepowerや重さweightなどとしてデータ解析を進める.解析の目的は,
- 走行距離と馬力(重さ)の関係性をみたい
- 車種の馬力(重さ)だけ与えられたときに,走行距離を予測できるか
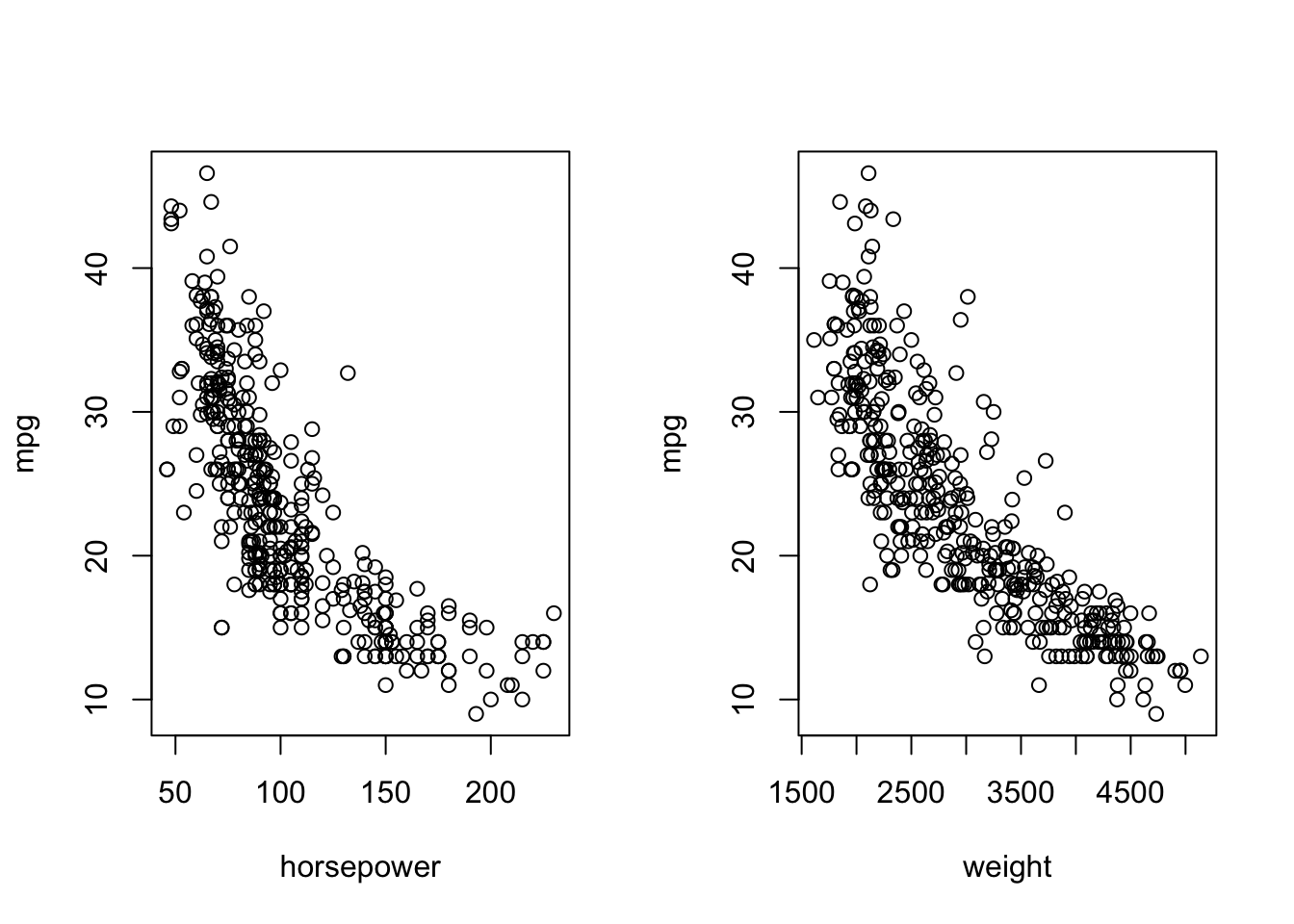
などであろう.まずは散布図を描いてデータを眺めてみる.
par(mfrow=c(1,2))
plot(Auto$horsepower, Auto$mpg, xlab="horsepower", ylab="mpg")
plot(Auto$weight, Auto$mpg, xlab="weight", ylab="mpg")
若干非線形的であるが,負の相関がどちらのケースも見て取れる.単回帰分析では,次のような線形モデルを仮定してデータ解析を進めていく.
\begin{align*}
Y = \beta_{0} + \beta_{1}X + \varepsilon,\quad \varepsilon \sim N(0, \sigma^{2})
\end{align*}
ここで,Yは走行距離に相当し,Xは馬力や重さなどに相当する.\beta_{0}を定数項,\beta_{1}を回帰係数とよぶ.また,\varepsilonは正規誤差を意味しており,Xに関する線形項に正規誤差が乗っかってYが発生したと仮定しているのである.例えばAutoデータセットに対して,
\begin{align*}
Y = 40 - 0.16X + \varepsilon,\quad \varepsilon \sim N(0, 4.8^{2})
\end{align*}
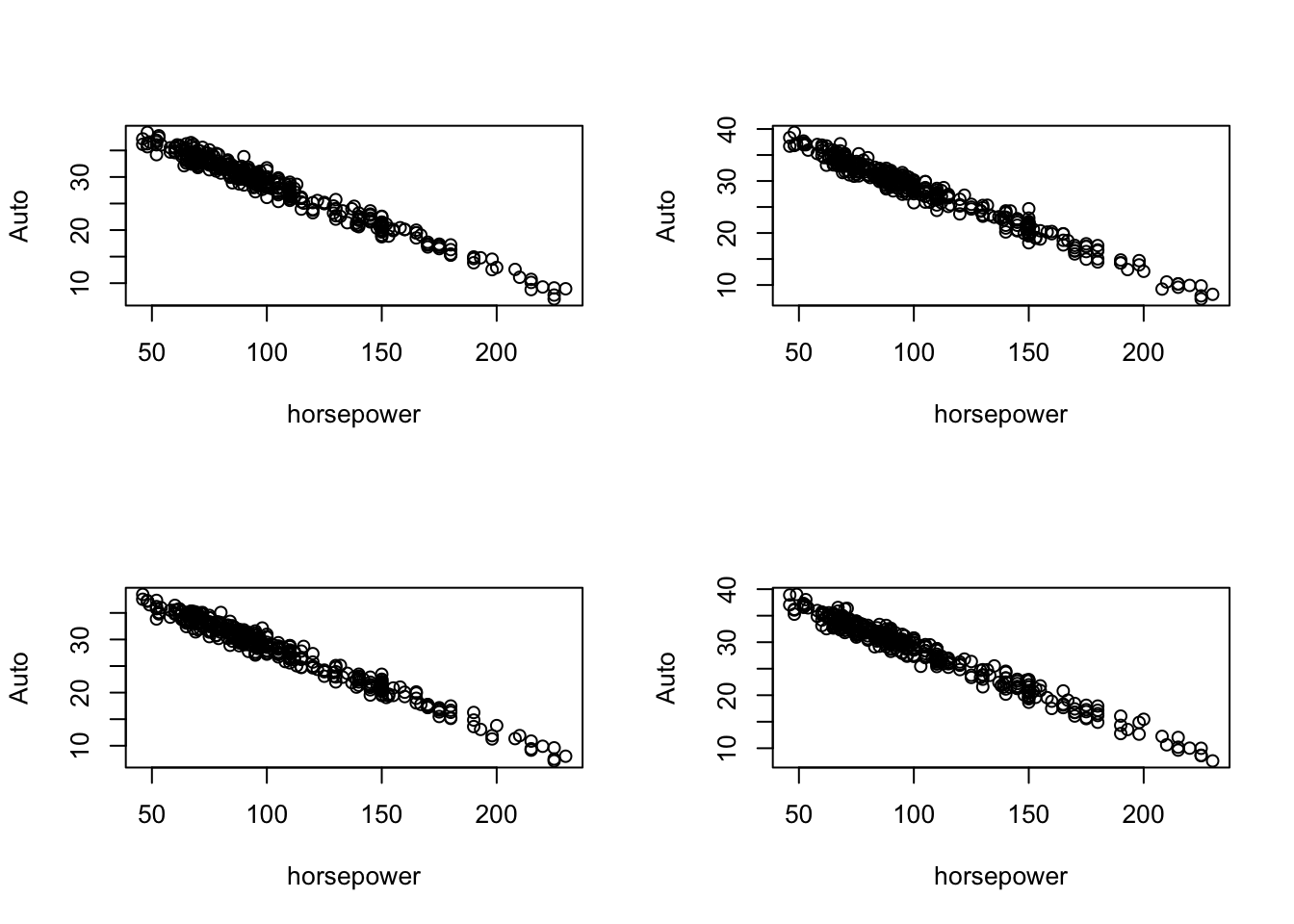
を仮定してみる.下記ではこのモデルに従って392個のYを4セット発生させ,それぞれ散布図を描いている.すなわち,実際の(horsepower, mpg)データは何セットか発生させた内のひとつの可能性として得られたものであると想定しているのである.
x <- as.vector(Auto$horsepower)
par(mfrow=c(2,2))
for(i in 1:4){
plot(x, 40 - 0.16*x + rnorm(392, 4.8), ylab="Auto", xlab="horsepower")
}
オリジナルの散布図との乖離は問題で,この実際とモデルの乖離が大きければ大きいほど,得られる結果も漠然としてものになる.
ところで,\beta_{0}や\beta_{1}の値はどうやって決定するのだろうか.これらは実際のデータから推定することができる.推定には最小二乗法を用いるのが一般的である.すなわち,結果変数と説明変数の組\{(y_{i}, x_{i})\}_{i=1}^{n}に対する回帰モデルとの誤差二乗和
\begin{align*}
\sum_{i=1}^{n}(y_{i} - \beta_{0} - \beta_{1}x_{i})^{2}
\end{align*}
を最小にするように定数項と回帰係数を推定するのである.推定値はそれぞれ\hat{\beta}_{0}, \hat{\beta}_{1}と書く.すなわち,
\begin{align*}
(\hat{\beta}_{0}, \hat{\beta}_{1}) =
\mathop{\rm argmin}\limits_{\beta_{0},\beta_{1}} \sum_{i=1}^{n}(y_{i} - \beta_{0} - x_{i}\beta_{1})^{2}
\end{align*}
である.ここで,argminは最小値を取る変数を返すものとする.
最小二乗法による推定値の計算やそれに基づく信頼区間の構成,検定などはlm関数を用いて簡単に実装できる.
result <- lm(mpg ~ horsepower, data=Auto)
summary(result)
Call:
lm(formula = mpg ~ horsepower, data = Auto)
Residuals:
Min 1Q Median 3Q Max
-13.5710 -3.2592 -0.3435 2.7630 16.9240
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 39.935861 0.717499 55.66 <2e-16 ***
horsepower -0.157845 0.006446 -24.49 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 4.906 on 390 degrees of freedom
Multiple R-squared: 0.6059, Adjusted R-squared: 0.6049
F-statistic: 599.7 on 1 and 390 DF, p-value: < 2.2e-16
lm関数におけるdata=の箇所にはデータフレーム形式のデータ行列を指定する必要がある. そのデータフレームの列名を使って,mpg ~ horsepowerの箇所で,結果変数をmpg,説明変数をhorsepowerとした 単回帰分析を実行している.結果の解釈は下図の通りである.


線形回帰分析において重要なパラメータは,説明変数に対する係数\beta_{1}である.これは回帰係数と呼ばれる.Section 3.2 より,その分布は,
\frac{\sqrt{n}(\hat{\beta}_{1}-\beta_{1})}{\sqrt{\hat{\sigma}^{2}/s_{x}^{2}}} \sim t_{n-2}
となる.ここで,t_{n-2}は自由度n-2のt分布であり,
s_{x}^{2} = \frac{1}{n}\sum_{i=1}^{n}(x_{i}-\bar{x}),\quad
\hat{\sigma}^{2} = \frac{1}{n-2}\sum_{i=1}^{n}(y_{i}-\hat{y}_{i}),\quad
\hat{y}_{i} = \hat{\beta}_{0} + \hat{\beta}_{1}x_{i}
である.帰無仮説H_{0} : \beta_{1}=0と対立仮説H_{1} : \beta_{1}\neq 0について, lm関数の結果として得られるt valueは
\frac{\sqrt{n}\hat{\beta}_{1}}{\sqrt{\hat{\sigma}^{2}/s_{x}^{2}}}
の観測値を示しており,Pr(>|t|)はこの観測値と分布t_{n-2}から計算されるp値を意味している.
定数項と回帰係数の推定値のみに興味がある場合は,残差のみに興味がある場合は次のように抽出できる.
coef(result) ##定数項と回帰係数の推定値
(Intercept) horsepower
39.9358610 -0.1578447
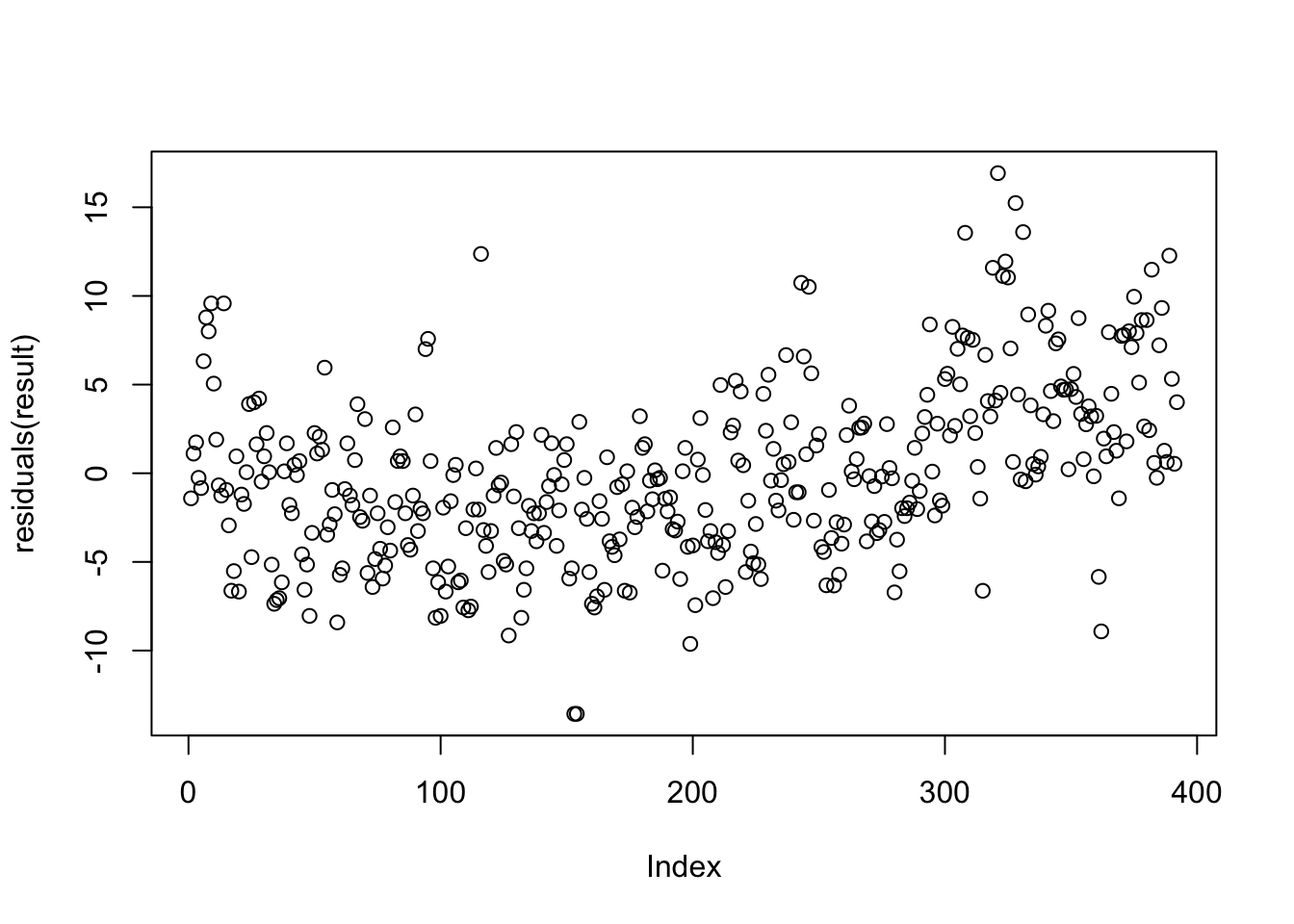
plot(residuals(result)) ##残差プロット
具体的な推定値の導出や,従う分布の導出などは Section 3.1 や Section 3.2 を参照のこと.
走行距離mpgを結果変数,説明変数を重さweightとし,散布図・最小二乗法による線形回帰・残差プロットを実行せよ.
Exercise 1.1で得られた散布図の中に回帰直線\hat{y} = \hat{\beta}_{0} + \hat{\beta}_{1}xを重ね書きせよ.なお,直線を描く関数はablineである.
多変量線形回帰分析
単回帰分析よりも複雑な現象を捉えるために,説明変数を複数にするのは自然であり合理的である.多変量線形回帰モデルは,
Y=\beta_{0} + \beta_{1}X_{1} + \beta_{2}X_{2} + \cdots + \beta_{p}X_{p} + \varepsilon,\quad \varepsilon\sim N(0,\sigma^{2})
であり,Autoデータの場合,例えば
{\tt mpg} = \beta_{0} + \beta_{1}{\tt horsepower} + \beta_{2}{\tt weight} + \varepsilon
といったモデルや,次のようなK次の多項式回帰が考えられる.
{\tt mpt} = \beta_{0} + \sum_{j=1}^{K}\beta_{j}({\tt horsepower})^{j} + \varepsilon
Rので実装は単回帰の場合と同様である.
result <- lm(mpg ~ horsepower + weight, data = Auto)
summary(result)
Call:
lm(formula = mpg ~ horsepower + weight, data = Auto)
Residuals:
Min 1Q Median 3Q Max
-11.0762 -2.7340 -0.3312 2.1752 16.2601
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 45.6402108 0.7931958 57.540 < 2e-16 ***
horsepower -0.0473029 0.0110851 -4.267 2.49e-05 ***
weight -0.0057942 0.0005023 -11.535 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 4.24 on 389 degrees of freedom
Multiple R-squared: 0.7064, Adjusted R-squared: 0.7049
F-statistic: 467.9 on 2 and 389 DF, p-value: < 2.2e-16
2次の多項式回帰は次のようになる.
result <- lm(mpg ~ horsepower + I(horsepower^2), data = Auto)
summary(result)
Call:
lm(formula = mpg ~ horsepower + I(horsepower^2), data = Auto)
Residuals:
Min 1Q Median 3Q Max
-14.7135 -2.5943 -0.0859 2.2868 15.8961
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 56.9000997 1.8004268 31.60 <2e-16 ***
horsepower -0.4661896 0.0311246 -14.98 <2e-16 ***
I(horsepower^2) 0.0012305 0.0001221 10.08 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 4.374 on 389 degrees of freedom
Multiple R-squared: 0.6876, Adjusted R-squared: 0.686
F-statistic: 428 on 2 and 389 DF, p-value: < 2.2e-16
多変量線形回帰の場合の最小二乗法を定式化するために,行列表記を準備しよう.
\begin{align*}
\bm{y} = \begin{pmatrix}y_{1}\\ y_{2}\\ \vdots \\ y_{n} \end{pmatrix},\quad
\bm{X} = \begin{pmatrix}
1 & x_{11} & \cdots & x_{1p} \\
1 & x_{21} & \cdots & x_{2p} \\
\vdots & \vdots & \vdots & \vdots \\
1 & x_{n1} & \cdots & x_{np}
\end{pmatrix},\quad
\bm{\beta} = \begin{pmatrix}\beta_{0} \\ \beta_{1} \\ \vdots \\ \beta_{p} \end{pmatrix}%,\quad
%\bm{\varepsilon} = \begin{pmatrix}\varepsilon_{1} \\ \varepsilon_{2} \\ \vdots \\ \varepsilon_{n} \end{pmatrix}
\end{align*}
ここで,(\bm{y}, \bm{X})は既知のものであり,推定したいものは\bm{\beta}である. また,任意のm次元ベクトル\bm{a} = (a_{1}, a_{2}, \dots, a_{m})^{T}について\ell_{2}ノルムを
\|\bm{a}\|_{2} = \sqrt{a_{1}^{2} + a_{2}^{2} + \cdots + a_{m}^{2}} = \sqrt{\bm{a}^{T}\bm{a}}
で定義する.単回帰の場合と同様,最小二乗法による推定値は,
\begin{align*}
(\hat{\beta}_{0}, \hat{\beta}_{1},\dots, \hat{\beta}_{p}) =
\mathop{\rm argmin}\limits_{\beta_{0},\beta_{1},\dots, \beta_{p}}\sum_{i=1}^{n}\bigg(y_{i} - \sum_{j=0}^{p}\beta_{j}x_{ij}\bigg)^{2}
\end{align*}
となる.ベクトル表記と\ell_{2}ノルムを使うと,
\sum_{i=1}^{n}\bigg(y_{i} - \sum_{j=0}^{p}\beta_{j}x_{ij}\bigg)^{2}=\|\bm{y} - \bm{X}\bm{\beta}\|_{2}^{2}
となるから,\hat{\bm{\beta}} = (\hat{\beta}_{0}, \hat{\beta}_{1},\dots, \hat{\beta}_{p})^{T}とおけば,
\hat{\bm{\beta}} = \mathop{\rm argmin}\limits_{\bm{\beta}} \|\bm{y} - \bm{X}\bm{\beta}\|_{2}^{2}
とシンプルに書ける.Section 3.3 より,推定値は陽に解けて,
\hat{\bm{\beta}} = (\bm{X}^{T}\bm{X})^{-1}\bm{X}^{T}\bm{y}
\tag{1}
となる.
Equation 1 を用いて,結果変数をmpg,説明変数をhorsepowerとweightとしたときの最小二乗法による推定値を計算せよ.
Appendix
推定値(単回帰)の導出
n個の結果変数と説明変数のペア\{(y_{i}, x_{i})\}_{i=1}^{n}に対して,最小二乗法による推定値は次で与えられる.
\begin{align*}
(\hat{\beta}_{0}, \hat{\beta}_{1}) =
\mathop{\rm argmin}\limits_{\beta_{0},\beta_{1}} L(\beta_{0},\beta_{1}),\quad
L(\beta_{0},\beta_{1}) = \sum_{i=1}^{n}(y_{i} - \beta_{0} - x_{i}\beta_{1})^{2}
\end{align*}
ここで,argminは最小値を取る変数を返すものとする.L(\beta_{0}, \beta_{1})は凸関数であり,極小点は
\begin{align*}
&\frac{\partial}{\partial \beta_{0}}L(\beta_{0},\beta_{1}) = -2\sum_{i=1}^{n}(y_{i}-\beta_{0}-x_{i}\beta_{1}) = 0\\
&\frac{\partial}{\partial \beta_{1}}L(\beta_{0},\beta_{1}) = -2\sum_{i=1}^{n}x_{i}(y_{i}-\beta_{0}-x_{i}\beta_{1}) = 0
\end{align*}
を満たす(\beta_{0},\beta_{1})である.いま,その極小点におけるヘッセ行列が正定値であるから,これは(\hat{\beta}_{0}, \hat{\beta}_{1})に一致する.第1式より,
\hat{\beta}_{0} = \bar{y} - \bar{x}\hat{\beta}_{1},\quad
\bar{y} = \frac{1}{n}\sum_{i=1}^{n}y_{i},\quad \bar{x} = \frac{1}{n}\sum_{i=1}^{n}x_{i}
であり,これを第2式に代入して整理すると,
\begin{align*}
\sum_{i=1}^{n}x_{i}\big\{ (y_{i}-\bar{y}) - (x_{i}-\bar{x})\hat{\beta}_{1} \big\} = 0
\end{align*}
となる.これを解けば,
\hat{\beta}_{1} = \frac{\sum_{i=1}^{n}x_{i}(y_{i}-\bar{y})}{\sum_{i=1}^{n}x_{i}(x_{i}-\bar{x})} = \frac{n^{-1}\sum_{i=1}^{n}(x_{i}-\bar{x})(y_{i}-\bar{y})}{n^{-1}\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}}
\tag{2}
を得る.すなわち,\hat{\beta}_{1}はXとYの共分散をXの分散で割ったものである.
分布(単回帰)の導出
正規誤差を伴う単回帰モデルを考える.
y_{i} = \beta_{0} + \beta_{1}x_{i} + \varepsilon_{i}
ここで,\varepsilon_{i}は独立に同一の正規分布N(0,\sigma^{2})に従うとする.このとき,Section 3.1 で求めた最小二乗推定量\hat{\beta}_{0}, \hat{\beta}_{1}の従う分布を導出しよう.
まずは\hat{\beta}_{1}の分布を導出する. 正規分布の性質から,定数c_{1},\dots, c_{n}に対して
\sum_{i=1}^{n}c_{i}\varepsilon_{i} \sim N\bigg(0, \sigma^{2}\sum_{i=1}^{n}c_{i}^{2}\bigg)
が成立する.s_{x}^{2} = \frac{1}{n}\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}, \bar{\varepsilon} = \frac{1}{n}\sum_{i=1}^{n}\varepsilon_{i}とおくと,Equation 2 より,
\begin{align*}
\hat{\beta}_{1} &= \frac{1}{ns_{x}^{2}}\sum_{i=1}^{n}\big(x_{i}-\bar{x})(\beta_{1}(x_{i}-\bar{x}) + \varepsilon_{i} - \bar{\varepsilon}\big) \\
&=\frac{\beta_1}{ns_{x}^{2}}\sum_{i=1}^{n}(x_{i}-\bar{x})^{2} + \frac{1}{ns_{x}^{2}}\sum_{i=1}^{n}(x_{i}-\bar{x})\varepsilon_{i} - \frac{\bar{\varepsilon}}{ns_{x}^{2}}\sum_{i=1}^{n}(x_{i} - \bar{x}) \\
&= \beta_{1} + \sum_{i=1}^{n}\frac{x_{i}-\bar{x}}{ns_{x}^{2}}\varepsilon_{i} - 0
\end{align*}
となる.いま,
\sum_{i=1}^{n}\frac{x_{i}-\bar{x}}{ns_{x}^{2}}\varepsilon_{i} \sim N\bigg(0,\frac{\sigma^{2}}{ns_{x}^{2}}\bigg)
だから,結局,
\hat{\beta}_{1} \sim N\bigg(\beta_{1}, \frac{\sigma^{2}}{ns_{x}^{2}}\bigg)
\tag{3}
を得る.同様にして,
\hat{\beta}_{0} \sim N\bigg(\beta_{0}, \frac{\sigma^{2}}{n}\bigg(1+\frac{\bar{x}^{2}}{s_{x}^{2}}\bigg)\bigg)
\tag{4}
が得られる.
(\hat{\beta}_{0}, \hat{\beta}_{1})の分布には未知の\sigma^{2}が含まれる.これは一般に未知であり,推定して代入する必要がある.しかしながら,\sigma^{2}の推定量を代入すると,従う分布が変わることに注意が必要である.誤差分散\sigma^{2}の不偏推定量は
\hat{\sigma}^{2} = \frac{1}{n-2}\sum_{i=1}^{n}(y_{i}-\hat{y}_{i})^{2},\quad
\hat{y}_{i} = \hat{\beta}_{0} + \hat{\beta}_{1}x_{i}
である.すなわち,E(\hat{\sigma}^{2}) = \sigma^{2}となっている.
Equation 3 および Equation 4 を標準化して\hat{\sigma}^{2}を代入したものの分布は, 正規分布ではなく自由度n-2のt分布となる.
\frac{\sqrt{n}(\hat{\beta}_{1}-\beta_{1})}{\sqrt{\hat{\sigma}^{2}/s_{x}^{2}}} \sim t_{n-2},
\tag{5}
\frac{\sqrt{n}(\hat{\beta}_{0}-\beta_{0})}{\sqrt{\hat{\sigma}^{2}(1+\bar{x}^{2}/s_{x}^{2})}} \sim t_{n-2}
\tag{6}
これらの導出は多変量のケースで統一的に行う.
推定値(多変量)の導出
一般に,関数f : \mathbb{R}^{p} \to \mathbb{R}に対する偏微分は,
\frac{\partial}{\partial \bm{\theta}}f(\bm{\theta}) = \begin{pmatrix}
\frac{\partial}{\partial \theta_{1}}f(\bm{\theta}) \\
\vdots \\
\frac{\partial}{\partial \theta_{p}}f(\bm{\theta})
\end{pmatrix}
で与えられる.まずは定数ベクトル\bm{a}=(a_{1},\dots, a_{p})とパラメータベクトル\bm{\theta}の 内積\bm{\theta}^{T}\bm{a}の偏微分を考える.第k要素\theta_{k}に関する偏微分は,
\frac{\partial}{\partial \theta_{k}}\bm{\theta}^{T}\bm{a}
=\frac{\partial}{\partial \theta_{k}}\sum_{j=1}^{p}\theta_{j}a_{j}=a_{k}
であるから,
\frac{\partial}{\partial \bm{\theta}}\bm{\theta}^{T}\bm{a} = \bm{a}
を得る.次に,p\times p対称行列A=(a_{ij})と\bm{\theta}の二次形式\bm{\theta}^{T}A\bm{\theta}の偏微分を考える.
\bm{\theta}^{T}A\bm{\theta} = \sum_{i=1}^{p}\sum_{j=1}^{p}a_{ij}\theta_{i}\theta_{j}
=\sum_{i=1}^{p}a_{ii}\theta_{i}^{2} + 2\sum_{i=1}^{p-1}\sum_{j=i+1}^{p}a_{ij}\theta_{i}\theta_{j}
であるからしたがって,
\frac{\partial}{\partial \theta_{k}}\bm{\theta}^{T}A\bm{\theta} = 2a_{kk}\theta_{k} + 2\sum_{j=1,j\neq k}^{p}a_{kj}\theta_{j} = 2\sum_{j=1}^{p}a_{kj}\theta_{j} = 2(A\bm{\theta})_{k}
を得る.最後の(A\bm{\theta})_{k}はベクトルA\bm{\theta}の第k成分を意味する.ゆえに,
\frac{\partial}{\partial \bm{\theta}}\bm{\theta}^{T}A\bm{\theta} = A\bm{\theta}
となる.
最小二乗推定量\hat{\bm{\beta}}は,
\frac{\partial}{\partial \bm{\beta}}\|\bm{y} - \bm{X}\bm{\beta}\|_{2}^{2} = \bm{0}
を満たす\bm{\beta}であるから,これを解けばよい.
\begin{align*}
\frac{\partial}{\partial \bm{\beta}}\|\bm{y} - \bm{X}\bm{\beta}\|_{2}^{2}
=\frac{\partial}{\partial \bm{\beta}}\big(\bm{\beta}^{T}\bm{X}^{T}\bm{X}\bm{\beta} - 2\bm{\beta}^{T}\bm{X}^{T}\bm{y}\big) = 2\bm{X}^{T}\bm{X}\bm{\beta} - 2\bm{X}^{T}\bm{y}
\end{align*}
であるから,Equation 1 を得る.