ロジスティック回帰

ロジスティック回帰分析の目的は，2値の結果変数Y\in\{0,1\}を説明変数Xから予測・推測するものである．具体的な結果変数としては，

製品を買う or 買わない
病気になる or ならない
有害サイトである or 無害である
破産する or しない

などが挙げられる．結果変数が2値であるので，基本的には，Xが与えられたときのY=1となる条件付き確率

P(Y=1|X) = 1-P(Y=0|X)

をデータから推定することになる．そしてその推定した値が1/2を超える場合にY=1と判断すれば良い．

1 単変量の場合

まずはロジスティック回帰分析が適用できそうなデータを眺めてみる．

  library(ISLR)
  head(Default)

  default student   balance    income
1      No      No  729.5265 44361.625
2      No     Yes  817.1804 12106.135
3      No      No 1073.5492 31767.139
4      No      No  529.2506 35704.494
5      No      No  785.6559 38463.496
6      No     Yes  919.5885  7491.559

このデータには，個人の特徴量(学生会員かどうか, カード借入金額，収入)とその個人が債務不履行(default)を起こしたかどうかが含まれている．変数defaultはYes or Noの2値であり，これを結果変数として，カード借入金額(balance)からの予測を考える．

変数defaultがfactor型であるため，これを1 or 0に数値化する．

  defa = data.frame(
    default = as.numeric(Default$default=="Yes"),
    balance = Default$balance,
    income = Default$income
    )
  head(defa)

  default   balance    income
1       0  729.5265 44361.625
2       0  817.1804 12106.135
3       0 1073.5492 31767.139
4       0  529.2506 35704.494
5       0  785.6559 38463.496
6       0  919.5885  7491.559

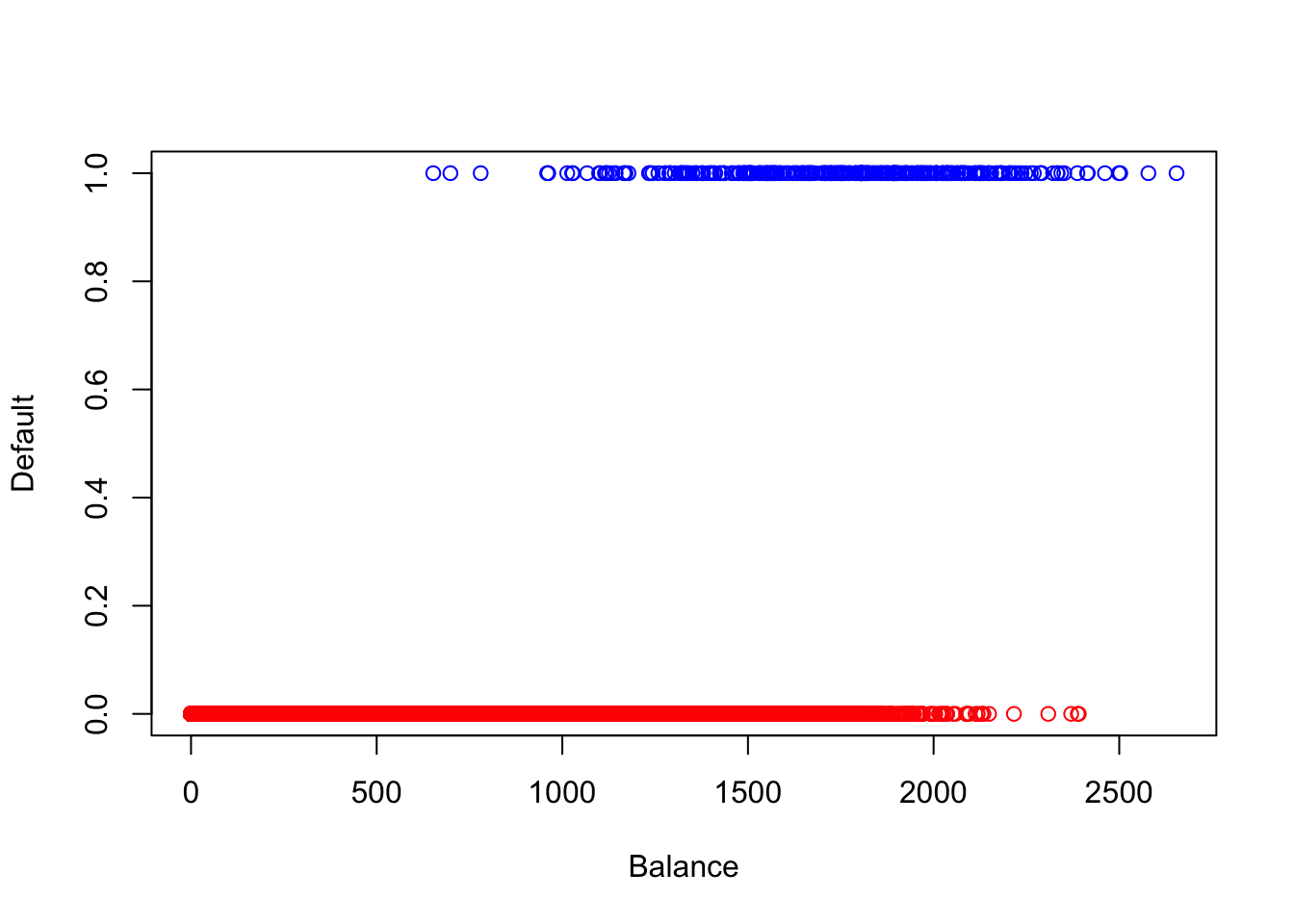
散布図を描いてデータの挙動を見てみる．x軸にbalance，y軸にdefaultを取るが，defaultは2値であるため0と1の箇所に張り付いたような散布図になる．カード借入金額が大きくなればなるほど債務不履行を起こしやすいことが見て取れる．

  plot(x=NULL,y=NULL,xlim=c(0,max(defa[,2]+1)),ylim=c(0,1),xlab="Balance",ylab="Default")  ##空のプロットエリアを作成
  points(defa[which(defa$default==1),2],defa[which(defa$default==1),1],col="blue")  ##Y=1のプロット
  points(defa[which(defa$default==0),2],defa[which(defa$default==0),1],col="red")  ##Y=0のプロット

いま，仮に線形回帰分析を当てはめてみるとどうなるだろうか．性能評価も行うため，データをトレーニングとテストに分割した上で実行してみる．

  defa.tr <- defa[1:9000,]
  defa.te <- defa[9001:10000,]

  reg.defa <- lm(default~balance,data=defa.tr)
  pre <- predict(reg.defa,defa.te)  ##予測値(連続)の計算
  pre2 <- as.numeric(pre > 0.5)  ##preを2値の予測値に変換
  table(defa.te[,1], pre2)  ##テストデータにおける結果変数と予測値のクロス集計表

クロス集計表を見ると，テストデータの全てをY=0と予測しており全く上手く機能していない．

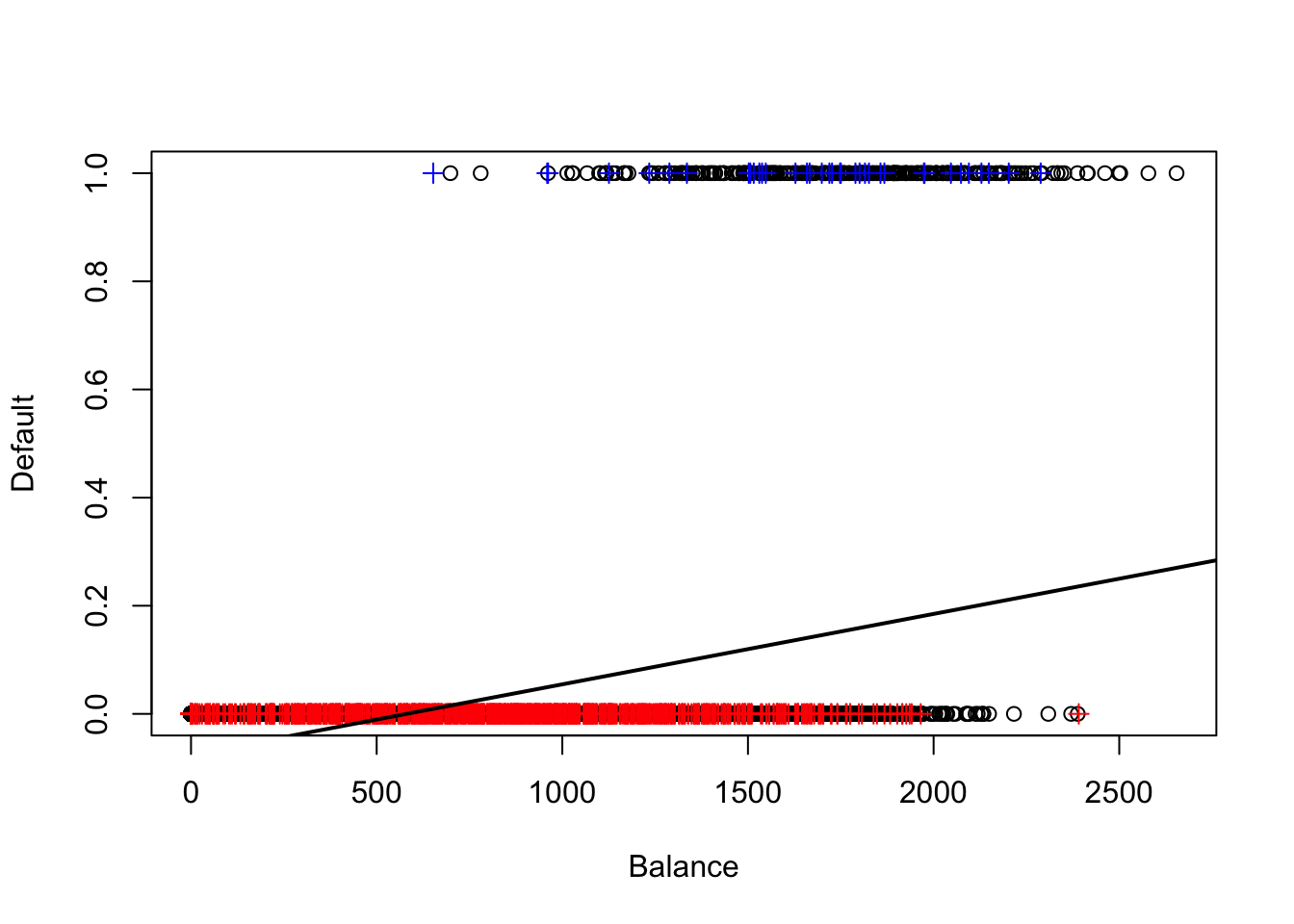
  plot(x=NULL,y=NULL,xlim=c(0,max(defa[,2]+1)),ylim=c(0,1),xlab="Balance",ylab="Default")
  points(defa.tr[which(defa.tr$default==1),2],defa.tr[which(defa.tr$default==1),1])
  points(defa.tr[which(defa.tr$default==0),2],defa.tr[which(defa.tr$default==0),1])
  points(defa.te[which(defa.te$default==1),2],defa.te[which(defa.te$default==1),1],col="blue",pch=3)  ##テストデータにおけるY=1のプロット
  points(defa.te[which(defa.te$default==0),2],defa.te[which(defa.te$default==0),1],col="red",pch=3)  ##テストデータにおけるY=0のプロット
  abline(coef(reg.defa)[1],coef(reg.defa)[2],lwd=2)  ##推定された回帰直線

上のプロットでは黒丸がトレーニングデータ，青と赤の十字がテストデータを意味している．回帰直線の値がそもそも0.5を超えていないため，上記のようなクロス集計表が得られたのだと考えられる．また，回帰直線は[0,1]の範囲を超えて値を取るため，結果変数が2値の場合には相応しくないように思える．

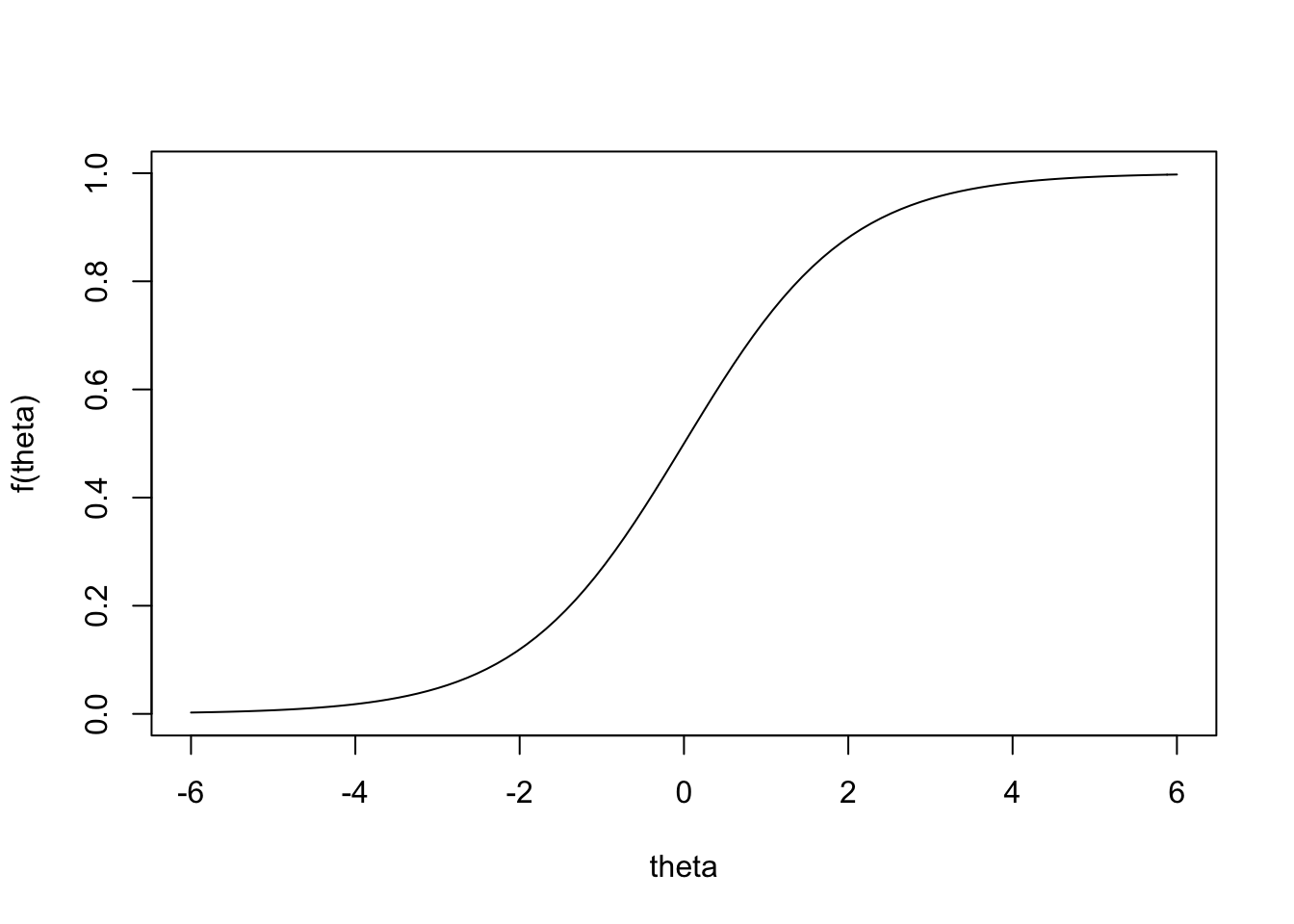
ロジスティック回帰では，次のロジスティック関数を元にP(Y=1|X)のモデルを作る．

f(\theta) = \frac{1}{1+\exp(-\theta)}

  curve(1/(1+exp(-x)),xlim=c(-6,6),ylim=c(0,1),ylab="f(theta)",xlab="theta")

このロジスティック関数の取る値は[0,1]を超えない．そして，パラメータ\thetaにXの線形関数を仮定したものが単変数の場合のロジスティック回帰モデルである．

P(Y=1|X) = \frac{1}{1+\exp\{-(\beta_{0} + \beta_{1}X)\}}

ここで，\beta_{0}と\beta_{1}はトレーニングデータ(y_{i}, x_{i})から推定する． Rを使った推定は非常に簡単である．それにはlm関数ではなく，glm関数を用いる．

  log.defa <- glm(default~balance,data=defa.tr,family="binomial")
  summary(log.defa)


Call:
glm(formula = default ~ balance, family = "binomial", data = defa.tr)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-2.2897  -0.1422  -0.0557  -0.0208   3.7175  

Coefficients:
              Estimate Std. Error z value Pr(>|z|)    
(Intercept) -10.817741   0.389584  -27.77   <2e-16 ***
balance       0.005596   0.000237   23.61   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 2610.4  on 8999  degrees of freedom
Residual deviance: 1402.1  on 8998  degrees of freedom
AIC: 1406.1

Number of Fisher Scoring iterations: 8

基本的な使い方はlm関数と同様であるが，family="binomial"と指定することでロジスティック回帰分析を実行する．

  pre <- predict(log.defa,defa.te,type="response") ##テストデータに対する予測値(確率)
  table(defa.te[,1],as.numeric(pre > 0.5))  ##クロス集計表

Y=1と予測するケースが線形回帰の場合と比べて増えたが，依然として債務不履行することがあまり当たっていない．債務不履行しないことは当たっているが，実際上あまり意味がない．

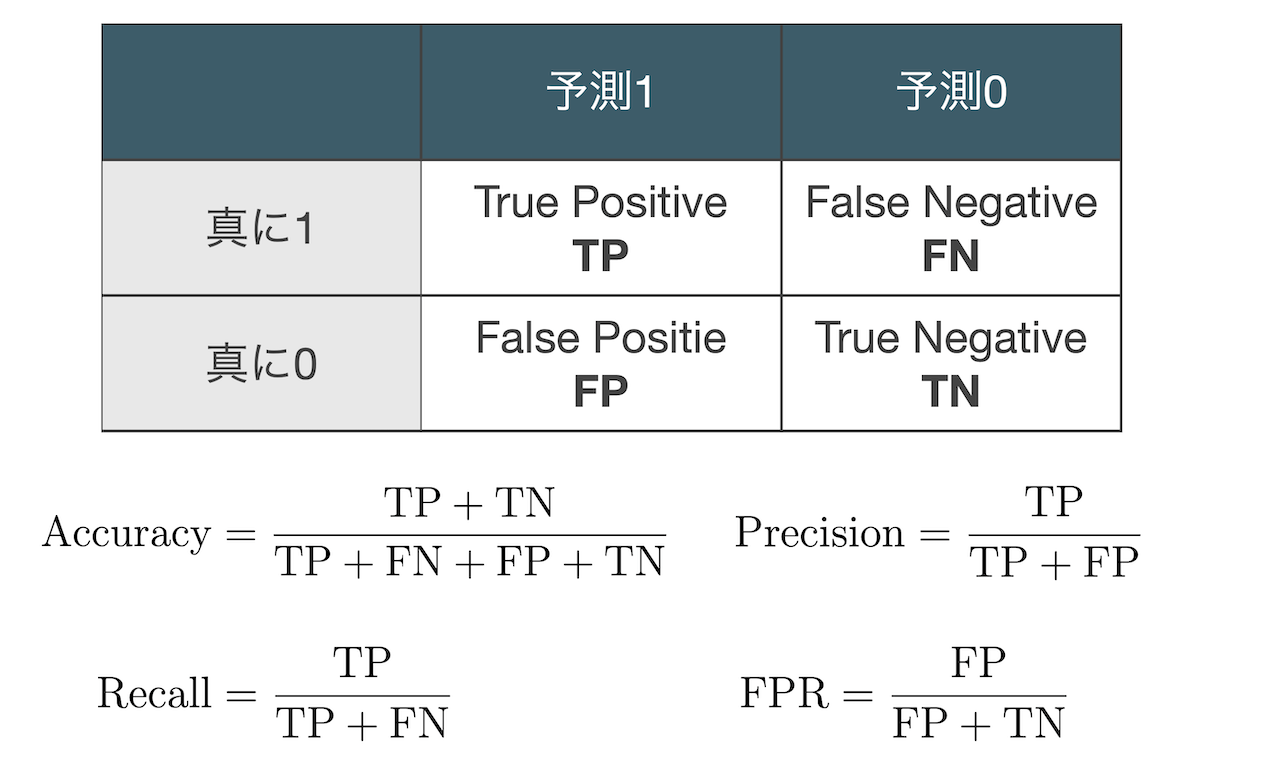
2 クロス集計表と性能指標

結果変数の真の値と予測値をクロス集計した表に関して，例えば次のような性能指標がある．ここで，例えば真に1と予測1がクロスするセルには，結果変数が真に1のときにモデルで1と予測されたサンプルの合計が入り，それはTrue positiveと呼ばれる．

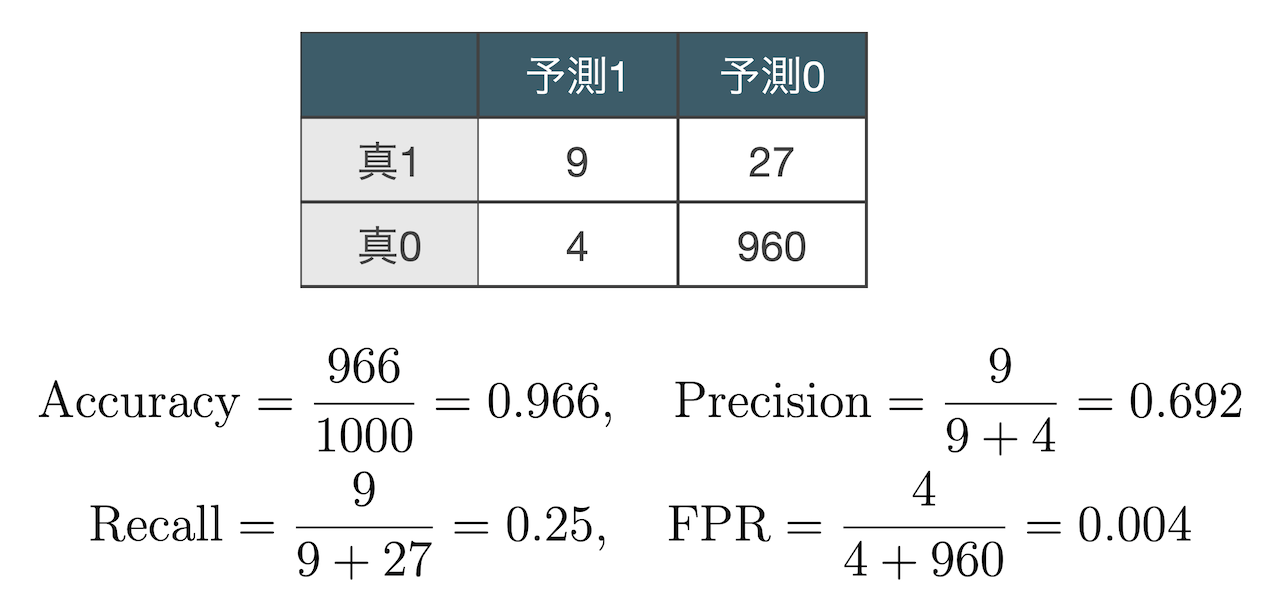
Defaultデータをロジスティック回帰で分析した際のクロス集計表は下記のようになる．

このデータは真に0であるサンプルが非常に多いアンバランスなデータであり，その情報が含まれている AccuracyとFPRは信頼できない．どちらの指標も(真0, 予測0)=960の影響がほとんどである．また，Recallが低いため，真に1であるサンプルの取りこぼしが多い．これは1だと予測したサンプルへと介入した際の効果が薄いことを意味している．一方，今回のデータではPrecisionがそこそこ高いが，もしこれが低かったとすると，介入した際のリスクが大きいことを意味している．

3 最尤法によるパラメータ推定

ロジスティック回帰モデルに含まれるパラメータ\beta_{0}, \beta_{1}の最尤法による推定を考える．最尤法は サンプルは確率最大のものが出現したという原理の下で行われる．例えばベルヌーイ分布の例を考えよう．

\begin{align*} X=\begin{cases} 1, &{\rm with\ probability\ }p \\ 0, &{\rm with\ probability\ }1-p \end{cases} \end{align*}

出現確率pが未知のベルヌーイ分布から，次の10個のサンプルが得られたとしよう．

\begin{align*} &x_{1}=1,x_{2}=0,x_{3}=0,x_{4}=1,x_{5}=1 \\ &x_{6}=1,x_{7}=0,x_{8}=1,x_{9}=1,x_{10}=1 \end{align*}

このサンプルが得られる確率を最大にするようにpを推定するのが最尤法である．いま，それぞれ独立にサンプルが得られたとすると，その同時確率は

\begin{align*} L(p) := p^{7}(1-p)^{3}= \textcolor{red}{\prod_{i=1}^{10}p^{x_{i}}(1-p)^{1-x_{i}}} \end{align*}

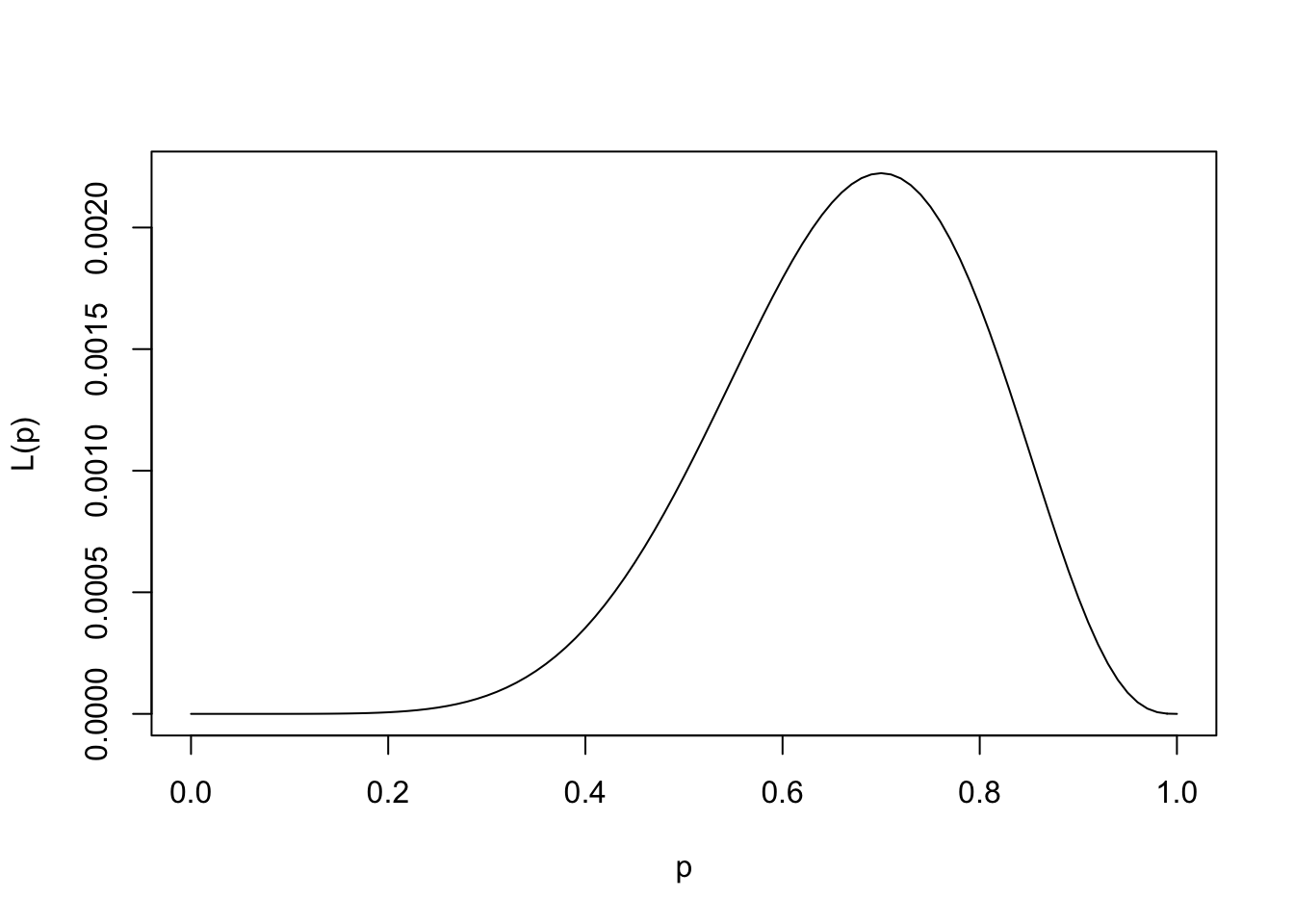
で与えられる．その関数形は次のようになる．

  Lp <- function(p){(p^7)*(1-p)^3}
  curve(Lp,xlim=c(0,1),xlab="p",ylab="L(p)")

そのため，関数L(p)の最大値を探せば良い．R上ではfor文を使って貪欲に最大値を探しても良いし， optimize関数を使うこともできる．

  optimize(Lp,interval=c(0,1),maximum=T)

$maximum
[1] 0.6999843

$objective
[1] 0.002223566

では，ロジスティック回帰モデルのパラメータを最尤法で推定してみよう．

\begin{align*} P(Y=1|X) =\textcolor{red}{p_{X}(\bm{\beta})} = \frac{1}{1+\exp(-\textcolor{blue}{\beta_{0}} - \textcolor{blue}{\beta_{1}}X)},\quad \bm{\beta} = (\beta_{0}, \beta_{1})^{T} \end{align*}

このモデルから独立にn個のサンプル(y_{1},x_{1}),\dots, (y_{n},x_{n})が得られたとする．このサンプルが得られる同時確率は

\begin{align*} L(\bm{\beta}) = \prod_{i=1}^{n}\{\textcolor{red}{p_{x_{i}}(\bm{\beta})} \}^{y_{i}}\{1-\textcolor{red}{p_{x_{i}}(\bm{\beta})}\}^{1-y_{i}} \end{align*}

となる．積を和に変換するために対数logを取ると(対数変換は単調のため推定値は変わらない)，以下の対数尤度関数の最大化問題を考えることになる．

\log L(\bm{\beta}) =\sum_{i=1}^{n}\big\{y_{i}\log p_{x_{i}}(\bm{\beta}) + (1-y_{i})\log (1-p_{x_{i}}(\bm{\beta}))\big\} \tag{1}

3.1 スコア法入門

上記のlog L(\bm{\beta})は2次元パラメータ\bm{\beta} = (\beta_{0}, \beta_{1})^{T}の関数であり，これを最大化するためには計算機的な方法が必要となる．ここでは，ニュートン法(統計分野ではスコア法)を紹介する．

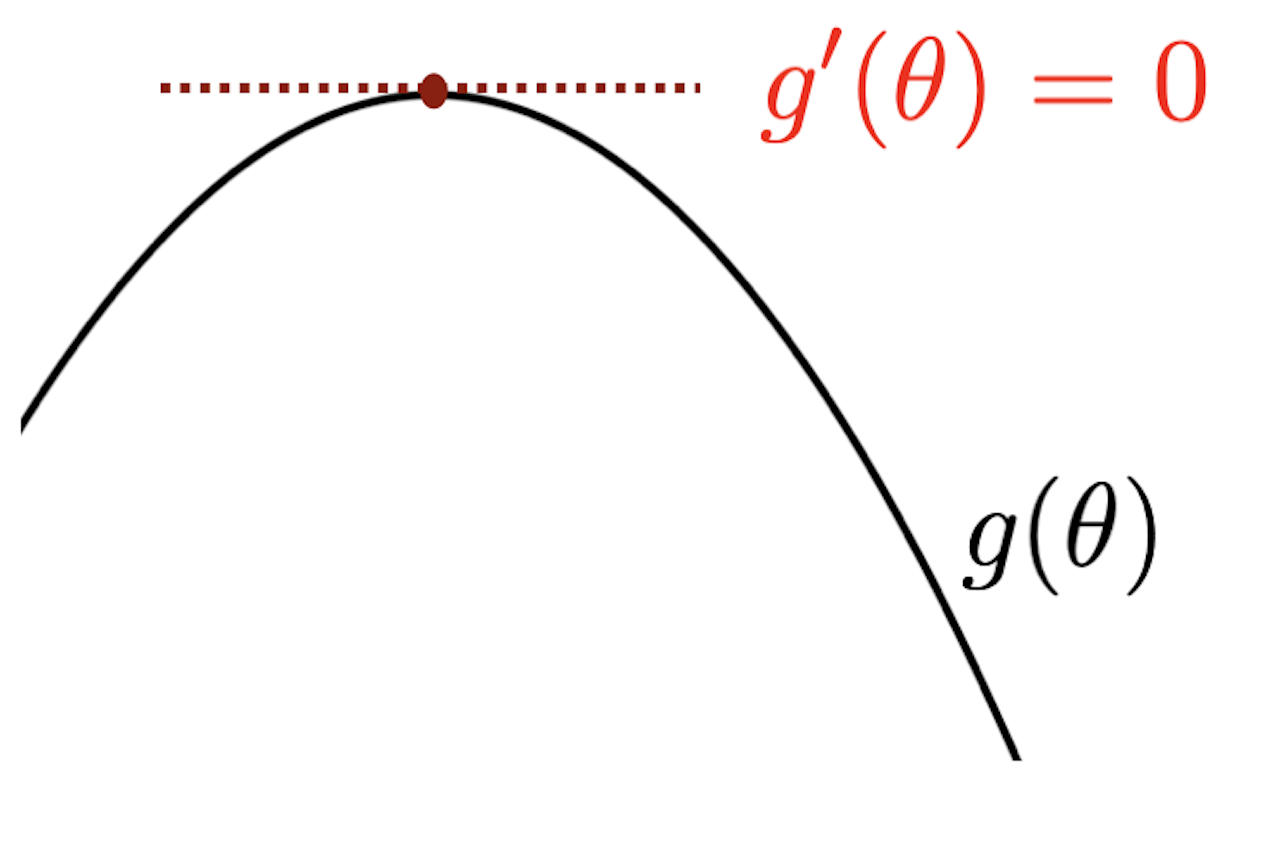
まずは1次元パラメータ\thetaを持つ関数g(\theta)のスコア法による最大化を考える．

スコア法はg'(\theta)=0となるパラメータ\thetaを求めるもので，適当な初期値\theta^{(0)}から順番に\theta^{(1)},\theta^{(2)},\dotsと更新していく．スコア法の基本的なアイデアはテーラー展開である．テーラー展開では，既知のg(\theta^{(0)})の値を使って\theta^{(0)}周辺でg(\theta)を近似している．

\begin{align*} g(\theta)=g(\theta^{(0)}) + g'(\theta^{(0)})(\theta-\theta^{(0)}) + \frac{1}{2}g''(\theta^{(0)})(\theta-\theta^{(0)})^{2}+\cdots \end{align*}

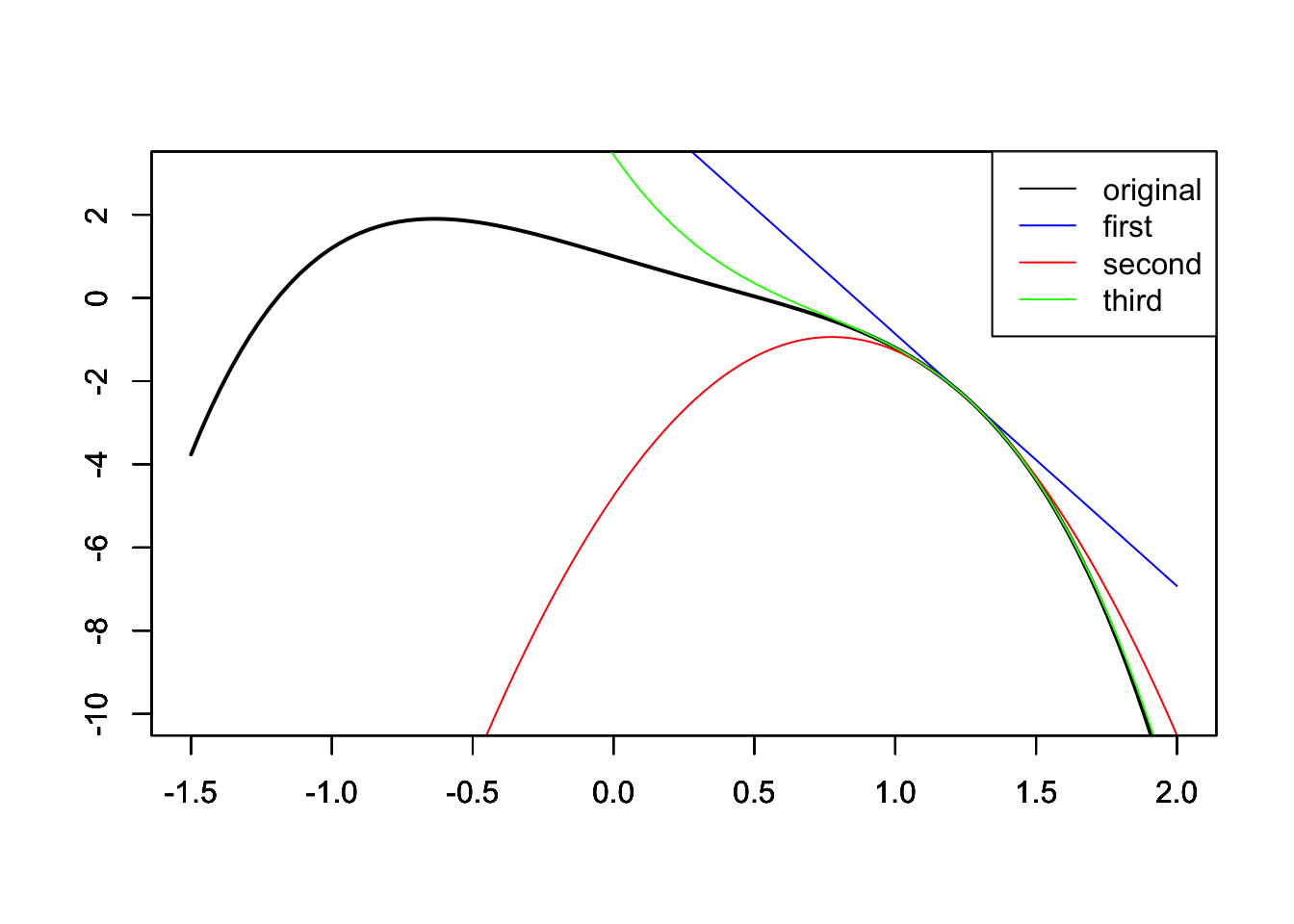
  g <- function(x){-x^4 + 0.8*x^3-2*x + 1}
  g1 <- function(x){-4*x^3 + 2.4*x^2 -2}
  g2 <- function(x){-12*x^2 + 4.8*x}
  g3 <- function(x){-24*x + 4.8}

  x0 <- 1.25
  ga1 <- function(x){g(x0) + g1(x0)*(x-x0)}
  ga2 <- function(x){g(x0) + g1(x0)*(x-x0) + 0.5*g2(x0)*(x-x0)^2}
  ga3 <- function(x){g(x0) + g1(x0)*(x-x0) + 0.5*g2(x0)*(x-x0)^2 + (1/6)*g3(x0)*(x-x0)^3}

  #draw
  curve(g,xlim=c(-1.5,2),ylim=c(-10,3),xlab="",ylab="",lwd=2)
  par(new=T)
  #first order approximation
  curve(ga1,xlim=c(-1.5,2),ylim=c(-10,3),xlab="",ylab="",col="blue")
  par(new=T)
  #second order approximation
  curve(ga2,xlim=c(-1.5,2),ylim=c(-10,3),xlab="",ylab="",col="red")
  par(new=T)
  #third order approximation
  curve(ga3,xlim=c(-1.5,2),ylim=c(-10,3),xlab="",ylab="",col="green")
  legend("topright",lty=1,col=c("black","blue","red","green"),legend=c("original","first","second","third"))

例えば上記の例では\theta^{(0)}=1.25から離れたところでの関数g(黒線)の近似は悪いが，\theta^{(0)}周辺では近似できている．

いま，関数G(\theta) = g'(\theta)に対して1次項までテーラー展開すると，

\begin{align*} g'(\theta) \simeq g'(\theta^{(0)}) + g''(\theta^{(0)})(\theta-\theta^{(0)}) \end{align*}

となる．左辺が0になるような\theta(これを\theta^{(1)}とおく)を求めれば，

\begin{align*} \theta^{(1)} = \theta^{(0)} - \frac{g'(\theta^{(0)})}{g''(\theta^{(0)})} \end{align*}

を得る．得られた\theta^{(1)}を使って同様に，

\begin{align*} \theta^{(2)} = \theta^{(1)} - \frac{g'(\theta^{(1)})}{g''(\theta^{(1)})} \end{align*}

を得る．以上のパラメータ更新を収束(値が変わらなくなる)まで繰り返す．

パラメータが2次元以上の場合は，テーラー展開が多次元のものに変わるだけである．すなわち，初期値\bm{\theta}^{(0)}を用いてG(\bm{\theta}) = \frac{\partial g(\bm{\theta})}{\partial \bm{\theta}}を1次までテーラー展開すると，

\frac{\partial g(\bm{\theta})}{\partial \bm{\theta}} \simeq \frac{\partial g(\bm{\theta}^{(0)})}{\partial \bm{\theta}} + \frac{\partial g(\bm{\theta}^{(0)})}{\partial\bm{\theta}\partial\bm{\theta}^{T}}(\bm{\theta}-\bm{\theta}^{(0)})

となる．ここで，q次元パラメータ\bm{\theta} = (\theta_{1},\dots, \theta_{q})^{T}について，

\frac{\partial g(\bm{\theta}^{(0)})}{\partial \bm{\theta}} =\bigg( \frac{\partial g(\bm{\theta}^{(0)})}{\partial \theta_{1}},\dots, \frac{\partial g(\bm{\theta}^{(0)})}{\partial \theta_{q}} \bigg)^{T}

であり，

\bigg( \frac{\partial g(\bm{\theta}^{(0)})}{\partial\bm{\theta}\partial\bm{\theta}^{T}} \bigg)_{jk} = \frac{\partial g(\bm{\theta}^{(0)})}{\partial \theta_{j}\partial \theta_{k}}

である．なお，(A)_{jk}は行列Aの(j,k)要素を意味する．よって\bm{\theta}^{(1)}への更新は以下のようになる．

\bm{\theta}^{(1)} = \bm{\theta}^{(0)} - \bigg(\frac{\partial g(\bm{\theta}^{(0)})}{\partial\bm{\theta}\partial\bm{\theta}^{T}}\bigg)^{-1}\frac{\partial g(\bm{\theta}^{(0)})}{\partial \bm{\theta}} \tag{2}

3.2 スコア法による最大化

ロジスティック回帰モデルの対数尤度関数 Equation 1 の最大化をスコア法で行う．Equation 2 の計算に必要なものを順番に求めよう．ロジスティック関数

f(\theta) = \frac{1}{1+\exp(-\theta)}

に対して，f'(\theta) = f(\theta)(1-f(\theta))である．p_{x_{i}}(\bm{\beta}) = f(\beta_{0} + \beta_{1}x_{i})であるから，

\begin{gather*} \frac{\partial p_{x_{i}}(\bm{\beta})}{\partial \beta_{0}} = f(\beta_{0} + \beta_{1}x_{i})(1-f(\beta_{0} + \beta_{1}x_{i})) = p_{x_i}(\bm{\beta})(1-p_{x_i}(\bm{\beta})) \\ \frac{\partial p_{x_{i}}(\bm{\beta})}{\partial \beta_{1}} = x_{i}f(\beta_{0} + \beta_{1}x_{i})(1-f(\beta_{0} + \beta_{1}x_{i})) = x_{i}p_{x_i}(\bm{\beta})(1-p_{x_i}(\bm{\beta})) \end{gather*}

を得る．よって，

\begin{align*} \frac{\partial \log L(\bm{\beta})}{\partial \beta_{0}} &= \sum_{i=1}^{n}\bigg\{y_{i}\frac{\partial \log p_{x_{i}}(\bm{\beta})}{\partial \beta_{0}} + (1-y_{i})\frac{\partial \log (1-p_{x_{i}}(\bm{\beta}))}{\partial \beta_{0}} \bigg\} \\ &=\sum_{i=1}^{n}\bigg\{y_{i}\frac{1}{p_{x_i}(\bm{\beta})}\frac{\partial p_{x_{i}}(\bm{\beta})}{\partial \beta_{0}} + (1-y_{i}) \frac{1}{1-p_{x_i}(\bm{\beta})} \frac{\partial (1-p_{x_{i}}(\bm{\beta}))}{\partial \beta_{0}} \bigg\} \\ &=\sum_{i=1}^{n}\bigg\{ y_{i}(1-p_{x_i}(\bm{\beta})) - (1-y_{i})p_{x_i}(\bm{\beta}) \bigg\} \\ &=\sum_{i=1}^{n}\big\{y_{i} - p_{x_i}(\bm{\beta})\big\} \end{align*}

であり，同様にして

\frac{\partial \log L(\bm{\beta})}{\partial \beta_{1}} = \sum_{i=1}^{n}x_{i}\big\{y_{i} - p_{x_i}(\bm{\beta})\big\}

を得る．ベクトル形式に直せば，

\frac{\partial \log L(\bm{\beta})}{\partial \bm{\beta}} = \bm{X}^{T}(\bm{y} - \bm{p}(\bm{\beta}))

となる．ただし，

\begin{align*} \bm{X}=\begin{pmatrix} 1 & x_{1} \\ 1 & x_{2} \\ \vdots & \vdots \\ 1 & x_{n} \end{pmatrix},\quad \bm{p}(\bm{\beta})=\begin{pmatrix} p_{x_1}(\bm{\beta}) \\ p_{x_2}(\bm{\beta}) \\ \vdots \\ p_{x_n}(\bm{\beta}) \end{pmatrix},\quad \bm{y}=\begin{pmatrix} y_{1} \\ y_{2} \\ \vdots \\ y_{n} \end{pmatrix} \end{align*}

である．次に2階微分に関する部分を計算しよう．

\begin{align*} &\frac{\partial \log L(\bm{\beta})}{\partial \beta_{0}^{2}} =\sum_{i=1}^{n}\frac{\partial}{\partial \beta_{0}}\big\{y_{i} - p_{x_i}(\bm{\beta})\big\} =-\sum_{i=1}^{n}p_{x_i}(\bm{\beta})(1-p_{x_i}(\bm{\beta})) \\ &\frac{\partial \log L(\bm{\beta})}{\partial \beta_{0}\partial\beta_{1}} =\sum_{i=1}^{n}\frac{\partial}{\partial \beta_{1}}\big\{y_{i} - p_{x_i}(\bm{\beta})\big\} =-\sum_{i=1}^{n}x_{i}p_{x_i}(\bm{\beta})(1-p_{x_i}(\bm{\beta})) \\ &\frac{\partial \log L(\bm{\beta})}{\partial \beta_{1}^{2}} =\sum_{i=1}^{n}\frac{\partial}{\partial \beta_{1}}x_{i}\big\{y_{i} - p_{x_i}(\bm{\beta})\big\} =-\sum_{i=1}^{n}x_{i}^{2}p_{x_i}(\bm{\beta})(1-p_{x_i}(\bm{\beta})) \end{align*}

となるからしたがって，

\frac{\partial \log L(\bm{\beta})}{\partial \bm{\beta}\partial \bm{\beta}^{T}} = - \bm{X}^{T}\bm{W}(\bm{\beta})\bm{X}

となる．ただし，

\bm{W}(\bm{\beta}) = \begin{pmatrix} p_{x_1}(\bm{\beta})(1-p_{x_1}(\bm{\beta})) & 0 & \cdots & 0 \\ 0 & p_{x_2}(\bm{\beta})(1-p_{x_2}(\bm{\beta})) & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & p_{x_n}(\bm{\beta})(1-p_{x_n}(\bm{\beta})) \end{pmatrix}

である．よって更新式は

\begin{align*} \bm{\beta}^{(1)} = \bm{\beta}^{(0)} - (\bm{X}^{T}\bm{W}(\bm{\beta}^{(0)})\bm{X})^{-1}\bm{X}^{T}(\bm{p}(\bm{\beta}^{(0)}) - \bm{y}) \end{align*}

で与えられる．対応するコードは下記になる．

  ff <- function(theta){1/(1+exp(-theta))}
  x <- defa.tr[,2]; X <- cbind(1,x); y <- defa.tr[,1]
  beta <- c(0,0); judge <- 1000

  for(k in 1:100){  #高々何回繰り返すかを指定
    if(judge >= 0.0001){  #値の更新がほとんど行われなくなったら終了
      old <- beta
      p <- ff(X%*%old)
      # H <- solve(t(X) %*% diag(c(p*(1-p))) %*% X) #これだと計算時間がかかる
      H <- solve(t(X) %*% (c(p*(1-p))*X))
      beta <- old - H %*% t(X) %*% (p-y)
      judge <- sum(abs(beta-old))
    } else break
  }

  beta

           [,1]
  -10.817741116
x   0.005595708

上記のコードでHを計算する際，\bm{X}^{T}\bm{W}(\bm{\beta}^{(0)})\bm{X}をひとつずつ積を取ると計算コストが高い．そのため，\bm{W}(\bm{\beta}^{(0)})\bm{X}を先に計算して行列のサイズを小さくしている．

Exercise 4.1

パラメータが\lambdaのポアソン分布は \begin{align*} P(X=k) = \frac{e^{-\lambda}\lambda^{k}}{x!},\quad k=1,2,\dots \end{align*} で与えられる．このとき，以下を実行せよ．

関数rpoisを用いて，\lambda=5のポアソン分布に従う乱数を500個発生させよ．
上で発生させたデータに対する対数尤度関数L(\lambda)を自作関数として定義せよ．
上で定義した関数の最大値をoptimize関数を利用して求めよ．
対数尤度関数L(\lambda)の最大値をスコア法で求めよ．

4 多変量の場合

説明変数が複数になった場合のロジスティック回帰モデルも同様に定義される．

\begin{align*} P(Y=1|X) = \frac{1}{1+\exp(-\beta_{0} - \beta_{1}X_{1}-\cdots -\beta_{p}X_{p})} \end{align*}

glm関数の使い方もlm関数の場合と同様である．例えばDefaultデータにおいて説明変数を balanceとincomeにする場合は次のように記述すれば良い．

  log.defa <- glm(default~balance+income,data=defa.tr,family="binomial")
  summary(log.defa)


Call:
glm(formula = default ~ balance + income, family = "binomial", 
    data = defa.tr)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-2.2387  -0.1391  -0.0540  -0.0196   3.7546  

Coefficients:
              Estimate Std. Error z value Pr(>|z|)    
(Intercept) -1.176e+01  4.704e-01 -25.001  < 2e-16 ***
balance      5.760e-03  2.452e-04  23.495  < 2e-16 ***
income       2.165e-05  5.308e-06   4.079 4.53e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 2610.4  on 8999  degrees of freedom
Residual deviance: 1385.4  on 8997  degrees of freedom
AIC: 1391.4

Number of Fisher Scoring iterations: 8

スコア法による最適化も，説明変数行列次のように拡大し，

\begin{align*} \bm{X}=\begin{pmatrix} 1 & x_{11} & x_{12} &\cdots &x_{1p} \\ 1 & x_{21} & x_{22} & \cdots & x_{2p}\\ \vdots & \vdots &\vdots & \cdots &\vdots \\ 1 & x_{n1} & x_{n2} &\cdots &x_{np} \end{pmatrix} \end{align*}

同様の更新を行えば良い．

\begin{align*} \bm{\beta}_{1} = \bm{\beta}_{0} - (\bm{X}^{T}\bm{W}(\bm{\beta}_{0})\bm{X})^{-1}\bm{X}^{T}(\bm{p}(\bm{\beta}_{0}) - \bm{y}) \end{align*}