Introduction to machine learning

統計的学習とは

• データを理解するためのツールの総称
• 教師あり学習と教師なし学習に大別される

	入力	出力	備考
教師あり	○	○	入力から出力を予測(or 推定)
教師なし	○	×	入力の構造を学習

教師あり学習

教師あり学習では，入力データと出力データの関係性fを明らかにすることが目的である．

• 入出力がそれぞれ多次元(多変数)になることもある
• 基本的に行なっているのはfの推定(学習と呼ばれることもある)

一般的な定式化

通常，入力は説明変数と呼ばれ，出力は結果変数(アウトカム)と呼ばれる．そして，p個の説明変数X=(X_{1},X_{2},\dots, X_{p})に対して結果変数Yがノイズ\varepsilonを伴って次のように得られたと仮定する．

\begin{align*} Y = f(X) + \varepsilon \end{align*}

ただし，

• 関数f(\cdot)は完全もしくは部分的に未知であり，データから推定する
• ノイズ\varepsilonは関数fで説明できない確率的な変動を意味している

例えば，MASSライブラリ内のBostonデータを見てみよう．

  library(MASS)
  head(Boston)

     crim zn indus chas   nox    rm  age    dis rad tax ptratio  black lstat
1 0.00632 18  2.31    0 0.538 6.575 65.2 4.0900   1 296    15.3 396.90  4.98
2 0.02731  0  7.07    0 0.469 6.421 78.9 4.9671   2 242    17.8 396.90  9.14
3 0.02729  0  7.07    0 0.469 7.185 61.1 4.9671   2 242    17.8 392.83  4.03
4 0.03237  0  2.18    0 0.458 6.998 45.8 6.0622   3 222    18.7 394.63  2.94
5 0.06905  0  2.18    0 0.458 7.147 54.2 6.0622   3 222    18.7 396.90  5.33
6 0.02985  0  2.18    0 0.458 6.430 58.7 6.0622   3 222    18.7 394.12  5.21
  medv
1 24.0
2 21.6
3 34.7
4 33.4
5 36.2
6 28.7

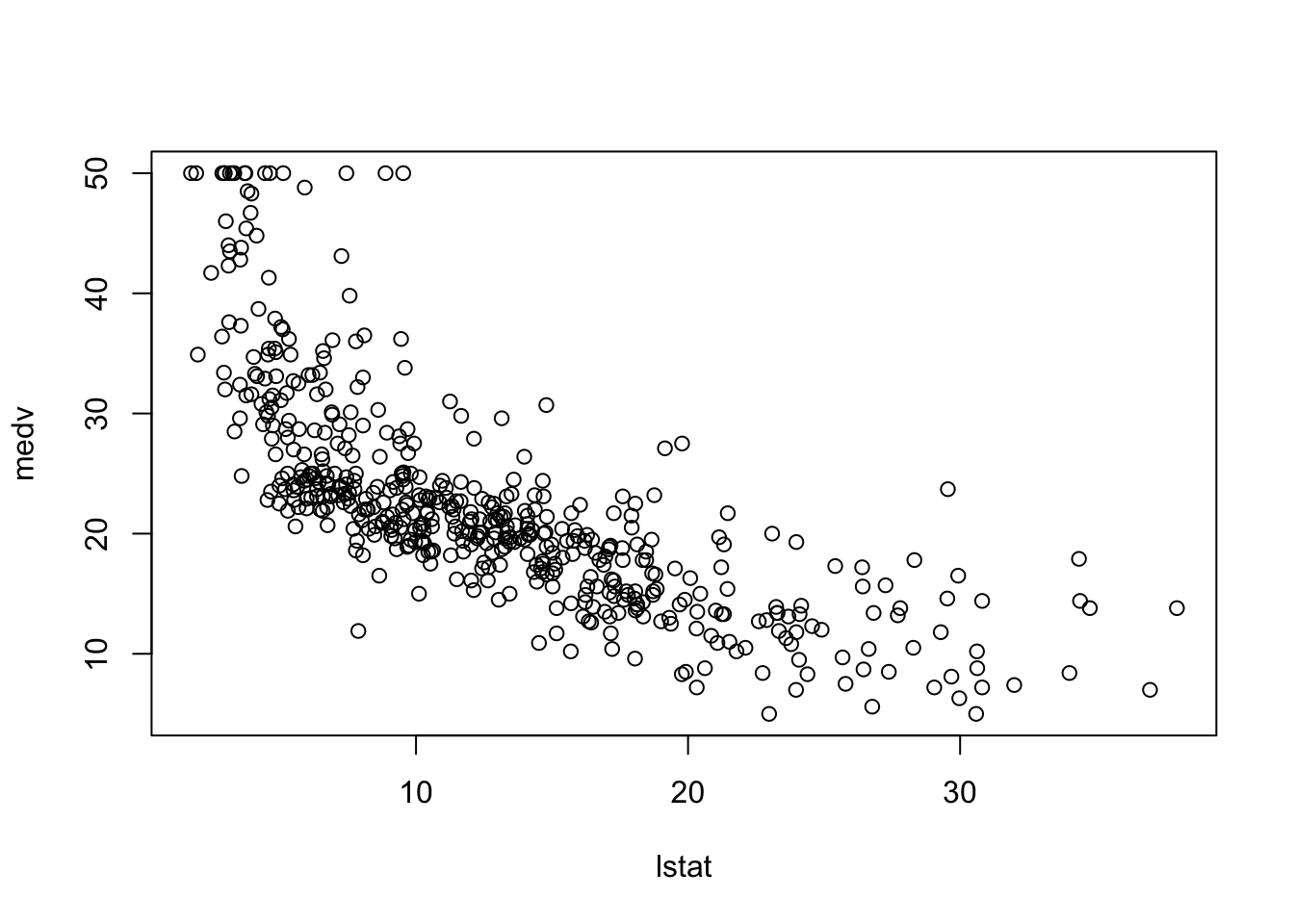
これはボストンの住宅価格に関するデータセットである． 住宅価格の中央値medvを低所得者の割合lstatから予測したい，もしくは，住宅価格に低所得者の割合がどのような影響を与えているかを知りたい場合，入力xをlstat，出力yをmedvとしてデータ解析を進める． 散布図を描くと次のようになる．

  x <- Boston$lstat; y <- Boston$medv
  plot(x, y, xlab="lstat", ylab="medv")

この散布図における各medvの値は，lstatに対する何らかの関数f({\tt lstat})にノイズが乗って得られたと仮定して，統計的学習，すなわちfの推定を進めていく．

教師あり学習の目的

教師あり学習は，分析者の意向によって，その目的が予測と推測に分かれる(両方のケースもあり得る)．

予測 \hat{Y} = \hat{f}(X)

• 関数fの推定というよりもそれを用いて予測される将来のYの値に興味がある
  • Ex. 株価予測，天気予報，画像判別
• 関数fの具体的な形状が分かる必要はない
  • Ex. 予測の精度さえ高ければ良い
• Xが簡単に得られる一方でYが難しい場合に特に有用
  • Ex. 血圧(X)と副作用の大きな薬への患者の反応(Y)
• 関連手法
  • ランダムフォレスト，スプライン回帰，ガウス過程回帰，深層学習など

推測

• 関数fの形状に興味があり，さらにXとYの関係性を考察したい
  • Ex. 広告費(X)と売上(Y)，景観(X)とマンション価格(Y)
• 関数fの形状まで仮定する必要がある <- モデルという
• 関連手法
  • 線形回帰，ロジスティック回帰，サポートベクトルマシンなど

ただし，これらの目的は基本的に同時達成できないことに注意が必要である．すなわち， 予測精度の向上と解釈可能性にはトレードオフが存在する．

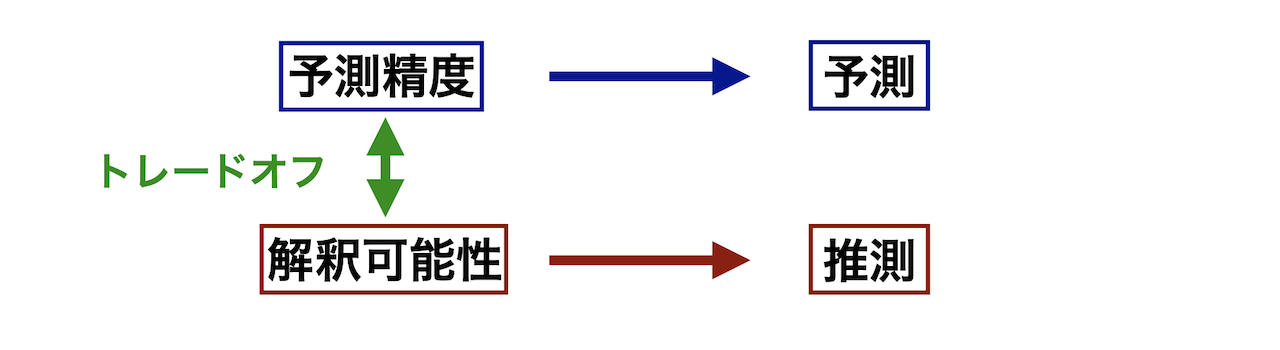
• 予測精度を向上させるためには…
  • 関数fを複雑にする(ブラックボックス化)
  • Ex. Y=\beta_{1}X_{1}^{2} + \beta_{2}\log X_{2} + \beta_{3}X_{1}^{1/5}|X_{3}| + \varepsilon
• 解釈可能性を高めるためには…
  • 関数fを簡潔に表す
  • Ex. Y=\beta_{1}X_{1} + \beta_{2}X_{2} + \beta_{3}X_{3} + \varepsilon

株価予測のためのデータセット作成

株価予測のために，まずは時系列の株価データを入出力の形式に整理する．ここで作成したデータは今後の統計的学習の際にもまた利用する予定である．

  library(quantmod)

 要求されたパッケージ xts をロード中です 

 要求されたパッケージ zoo をロード中です 

 次のパッケージを付け加えます: 'zoo' 

 以下のオブジェクトは 'package:base' からマスクされています: 

     as.Date, as.Date.numeric 

 要求されたパッケージ TTR をロード中です 

Registered S3 method overwritten by 'quantmod':
  method            from
  as.zoo.data.frame zoo 

  library(XML)

任天堂の株価を1年間程度取得する．

    nintendo <- getSymbols("7974.t", src = "yahooj", from = "2023-01-04", to="2024-04-10", auto.assign = FALSE)
    dnintendo <- fortify.zoo(nintendo)  ##dataframeに変換する．パッケージzooの関数fortify.zooを利用
    names(dnintendo) <- c("data","open","high","low","close","volume","adjusted")
    head(dnintendo)

        data open high  low close  volume adjusted
1 2023-01-04 5444 5546 5405  5487 5632900     5487
2 2023-01-05 5517 5603 5496  5530 4229200     5530
3 2023-01-06 5466 5483 5407  5483 5181300     5483
4 2023-01-10 5483 5565 5470  5470 5620700     5470
5 2023-01-11 5497 5548 5482  5547 5320000     5547
6 2023-01-12 5469 5488 5436  5447 7380700     5447

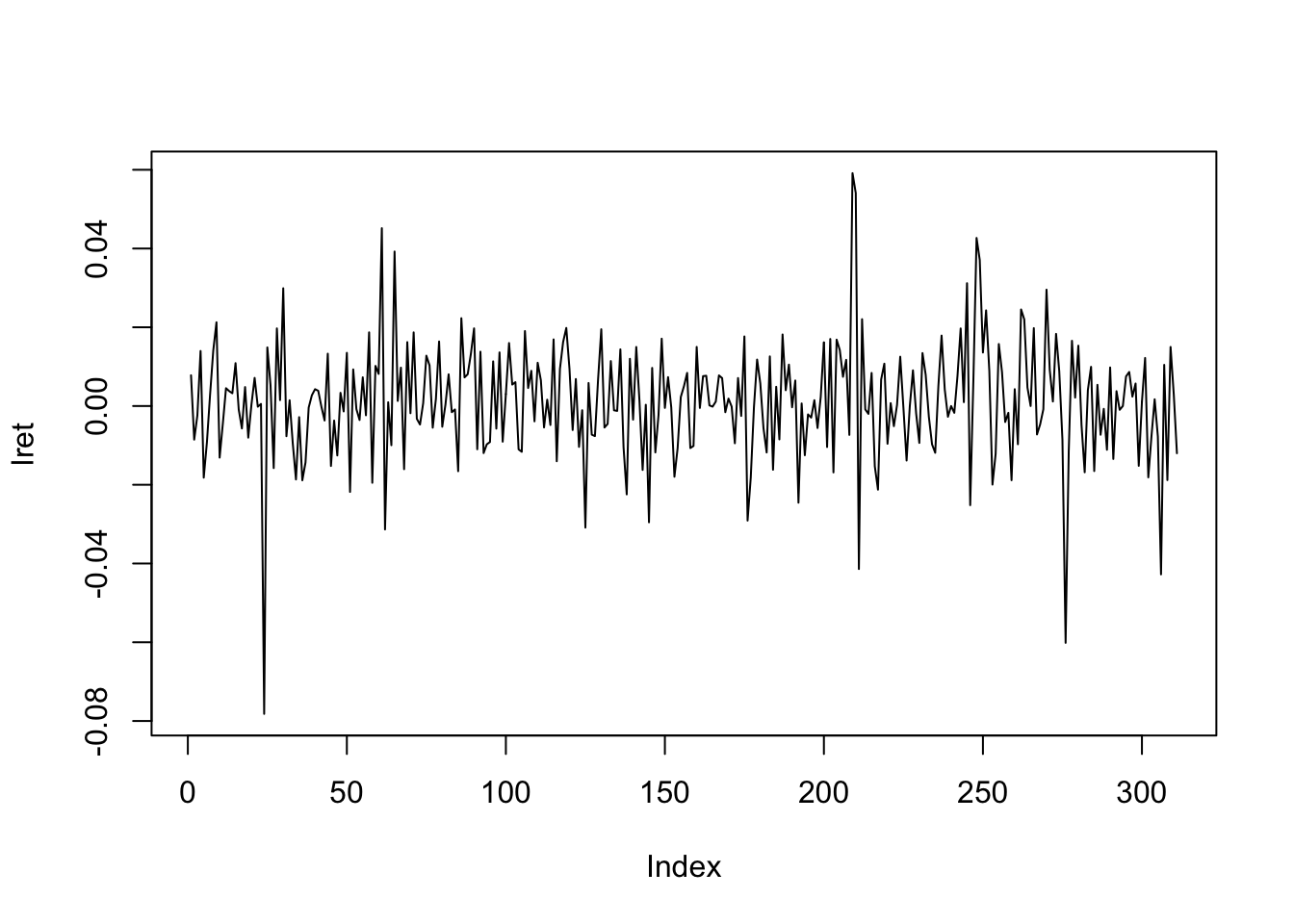
今回は終値だけに注目し，対数収益率\log(x_{t}) - \log(x_{t-1})に基づいて予測を行う． ここで，x_{t}はt時点における終値を意味する．差分系列の計算にはdiff関数が便利である．

  lret <- diff(log(dnintendo$close))
  plot(lret,type="l")

上記で説明した教師あり学習のフレームワークに落とすためには，入力と出力のペアが必要となってくる． ここでは，時点tにおける対数収益率を出力とし，そこからl時点前までの対数収益率をl次元の入力としよう．

  cnintendo <- data.frame(matrix(ncol=6,nrow=0))  ##空のデータフレームを作成(l=5)
  for(i in 1:(length(lret) - 5)){  ##for文を動かせる範囲に注意が必要
    new <- c(lret[i:(i+4)],lret[i+5])  ##最初の5つがx，残りがyに該当
    cnintendo <- rbind(cnintendo,new)
  }
  colnames(cnintendo) <- c("x1","x2","x3","x4","x5","y")  ##列名を適当に決めておく
  head(round(cnintendo,4))

       x1      x2      x3      x4      x5       y
1  0.0078 -0.0085 -0.0024  0.0140 -0.0182 -0.0092
2 -0.0085 -0.0024  0.0140 -0.0182 -0.0092  0.0030
3 -0.0024  0.0140 -0.0182 -0.0092  0.0030  0.0141
4  0.0140 -0.0182 -0.0092  0.0030  0.0141  0.0213
5 -0.0182 -0.0092  0.0030  0.0141  0.0213 -0.0131
6 -0.0092  0.0030  0.0141  0.0213 -0.0131 -0.0045

対数収益率自体に興味はなく，その正負にのみ興味がある場合もあるだろう．そのために，yを2値(0 or 1で1が正に対応)に変換したものも追加しておく.

  y2 <- (sign(cnintendo$y) + 1) / 2  ##yの符号だけ取り出して+1して-1を0に変換後，2で割る
  cnintendo <- cbind(cnintendo, y2)
  head(round(cnintendo,4))

       x1      x2      x3      x4      x5       y y2
1  0.0078 -0.0085 -0.0024  0.0140 -0.0182 -0.0092  0
2 -0.0085 -0.0024  0.0140 -0.0182 -0.0092  0.0030  1
3 -0.0024  0.0140 -0.0182 -0.0092  0.0030  0.0141  1
4  0.0140 -0.0182 -0.0092  0.0030  0.0141  0.0213  1
5 -0.0182 -0.0092  0.0030  0.0141  0.0213 -0.0131  0
6 -0.0092  0.0030  0.0141  0.0213 -0.0131 -0.0045  0

Exercise

好きな銘柄の株価を取得し，l=10で同様のデータセットを作成せよ．

なお，結果変数が対数収益率のような連続値の場合，その学習問題は回帰問題と呼ばれ，2値もしくは多値の場合，分類問題と呼ばれる．

教師なし学習

これは，入力のみが与えられ，それが持つ構造自体を学習する問題である．基本的には次元圧縮やクラスタリング等が主な解析となる．

例えば次のデータは64個のがん細胞株に対する6830個の遺伝子発現量であり，変数の次元(6830)が大きすぎてデータの特徴が把握しにくい．そのため，後で紹介する主成分分析などの方法を用いて，6830次元を2次元に次元圧縮する．

  library(ISLR)  ##パッケージISLRをインストール後，読み込む
  dim(NCI60$data)  ##遺伝子発現量のデータ

[1]   64 6830

  X <- scale(NCI60$data)
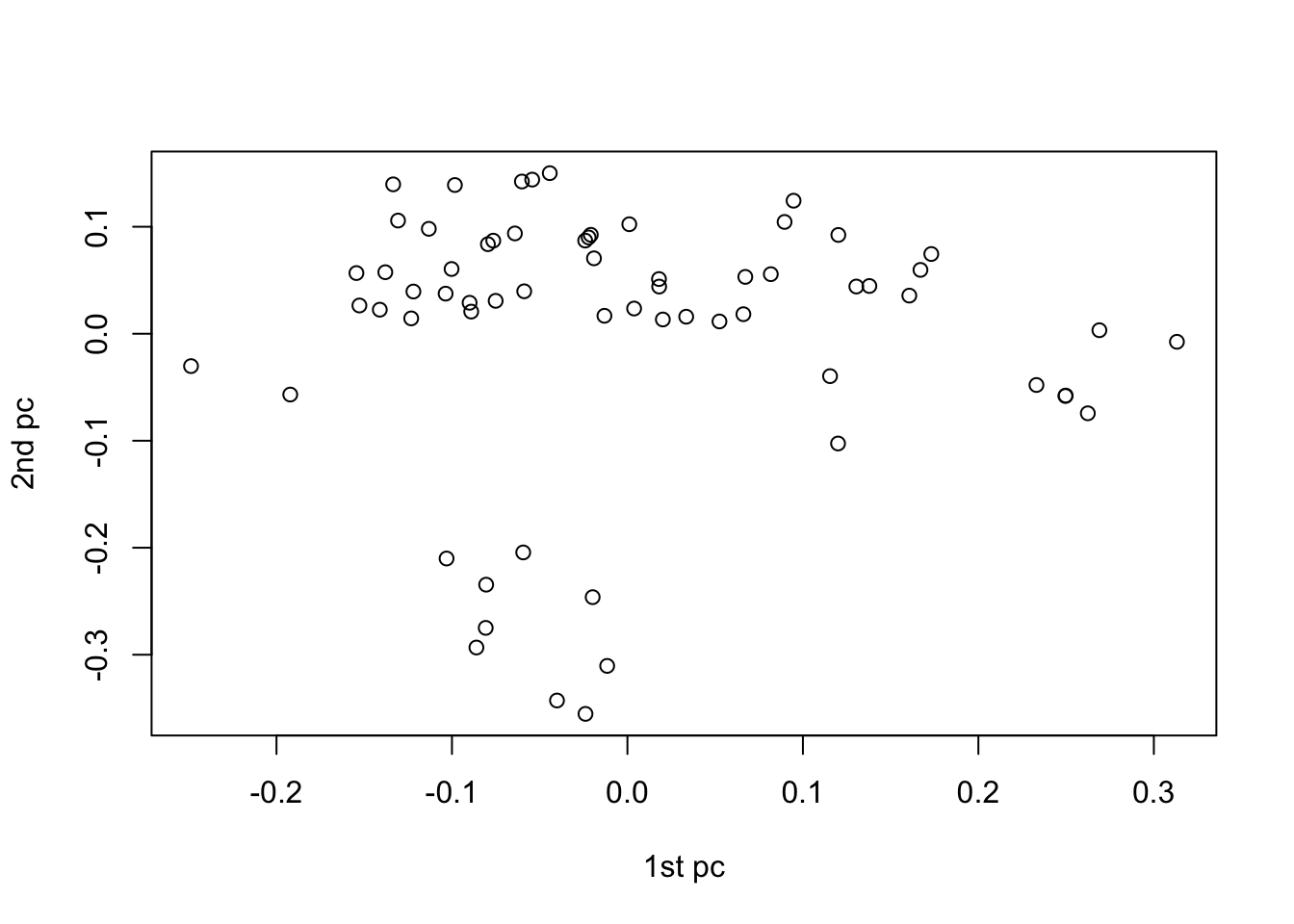
  re <- svd(X)
  plot(re$u[,1],re$u[,2],xlab="1st pc",ylab="2nd pc")

このように，データを2次元に圧縮したことで，それが持つ構造が少しわかりやすくなる．

Summary

統計的学習の分類

• 教師あり学習と教師なし学習
  • 出力があるかどうかで分類される

教師あり学習

• 予測と推測
  • どちらか一方しか精度向上できない(トレードオフ)
• 回帰問題と分類問題
  • 出力が連続値であるか離散であるかで分類される

教師なし学習

• 出力がない入力だけのデータ
• 主に次元圧縮やクラスタリングによって解析され，その構造理解が目的